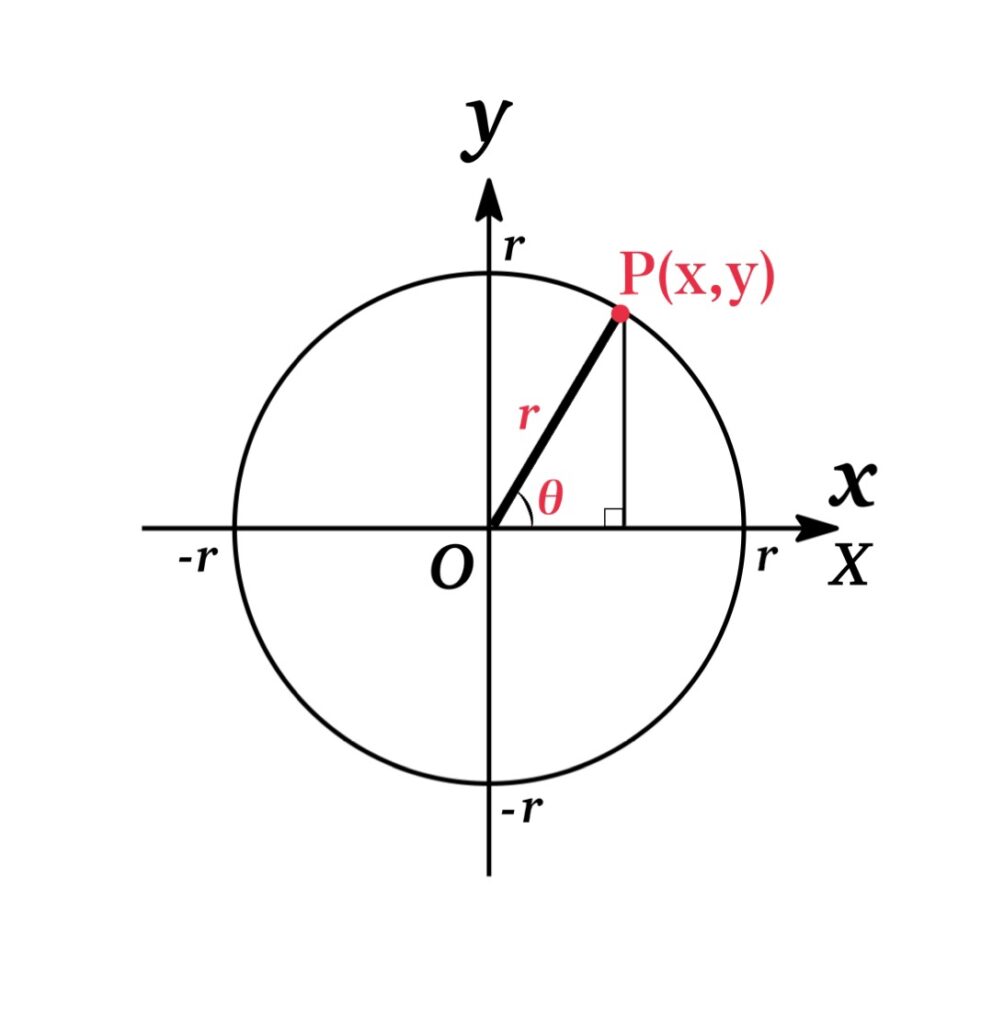
$x$ 軸の正部分を始線として角 $\theta$ の動径と原点 O を中心とする 半径 $r$ の円 との交点を $P(x,y)$ とする. このとき $\theta$ の正弦 ( $\sin \theta$ ) , 余弦 ( $\cos\theta$ ), 正接 ( $\tan \theta$ ) を次のように定義する :
$$\sin \theta=\frac{y}{r},\ \ \ \cos \theta=\frac{x}{r}, \ \ \ \tan \theta=\frac{y}{x}$$
このように定義すれば, $\sin\theta,\ \cos \theta, \ \tan \theta$ は $\theta$ の関数となり, これらをまとめて三角関数という.
上の三角関数公式と同様に、他の関数も定義される. ご参考までに.
$$\mathrm{csc}\ x=\frac{1}{\sin x}, \ \ \ \mathrm{sec}\ x=\frac{1}{\cos x},\ \ \ \mathrm{cot}\ x=\frac{1}{\tan x}$$
Contents
公式まとめ
相互関係式
| $\tan x=\frac{\sin x}{\cos x}$ | |
| $\sin^{2} x+\cos^{2} x=1$ | |
| $1+\tan^{2} x=\frac{1}{\cos^{2} x}$ |
グラフ
| 周期 | 対称 | |
| $y=\sin \theta$ | $360^{\circ}$ | 原点対称 |
| $y=\cos \theta$ | $360^{\circ}$ | y 軸対称 |
| $y=\tan \theta$ | $180^{\circ}$ | 原点対称 |
符号
$\theta$ がどの象限の角であるかによって, 三角関数の符号が決まる. 例えば $0\leq \theta\leq 180^{\circ}$ の場合, $0 \leq\sin \theta\leq 1$ より $\sin \theta$ の符号は + となる.
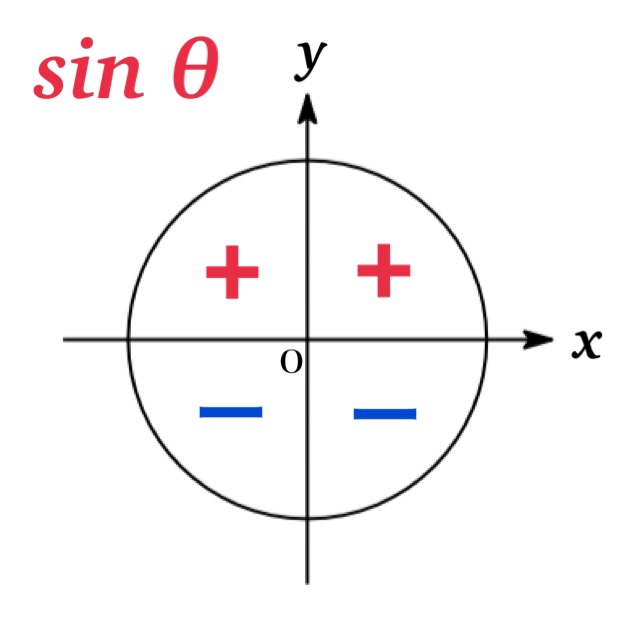
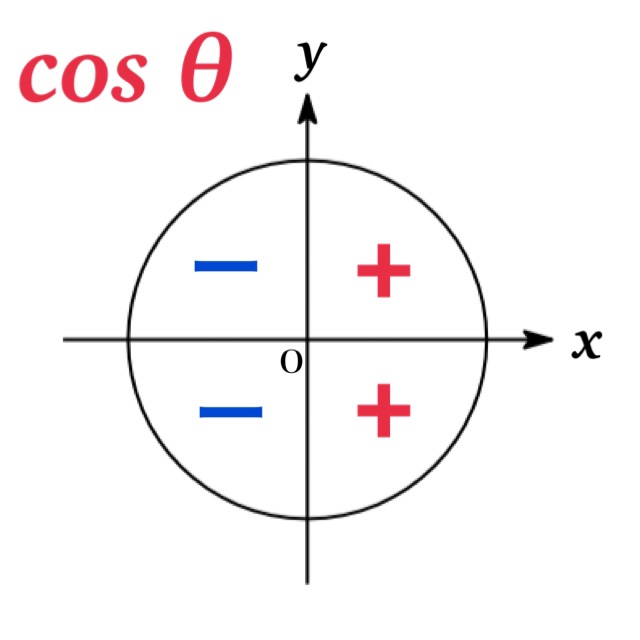
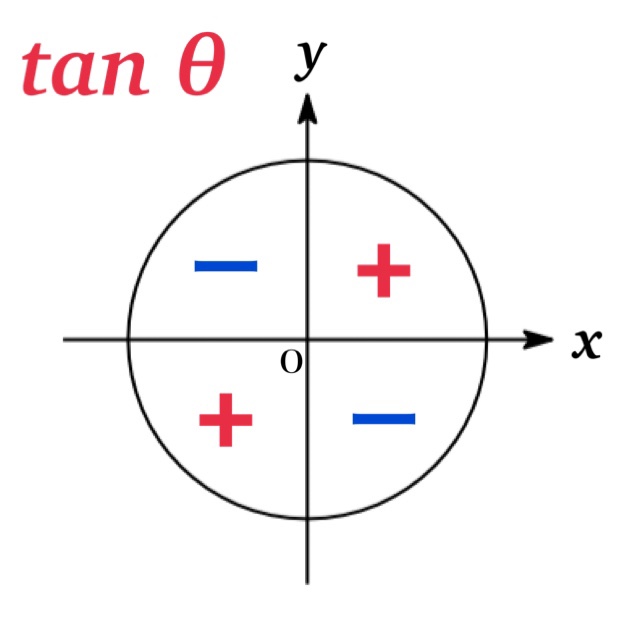
偶関数・奇関数
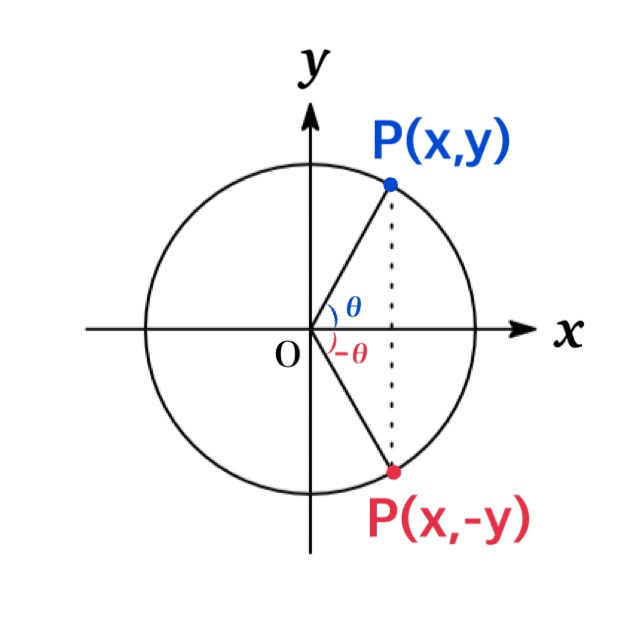
| $\sin (-x)=-\sin x$ | 奇関数(原点対称) |
| $\cos (-x)=\cos x$ | 偶関数( y 軸対称) |
| $\tan (-x)=-\tan x$ | 奇関数(原点対称) |
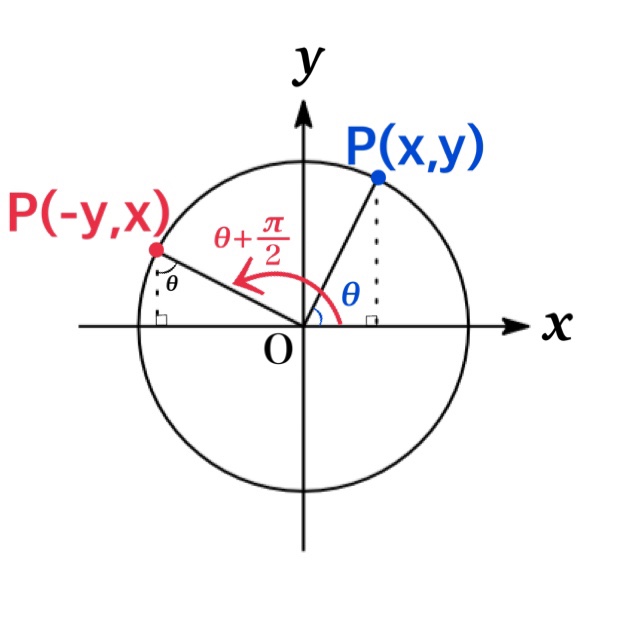
$(90^{\circ}\times m)+\theta$ の三角関数
| ($\theta+\frac{\pi}{2}$)の三角関数 | |
| $\sin(90^{\circ}+\theta)=\cos \theta$ | |
| $\cos(90^{\circ}+\theta)=-\sin \theta$ | |
| $\tan(90^{\circ}+\theta)=-\frac{1}{\tan \theta}$ |
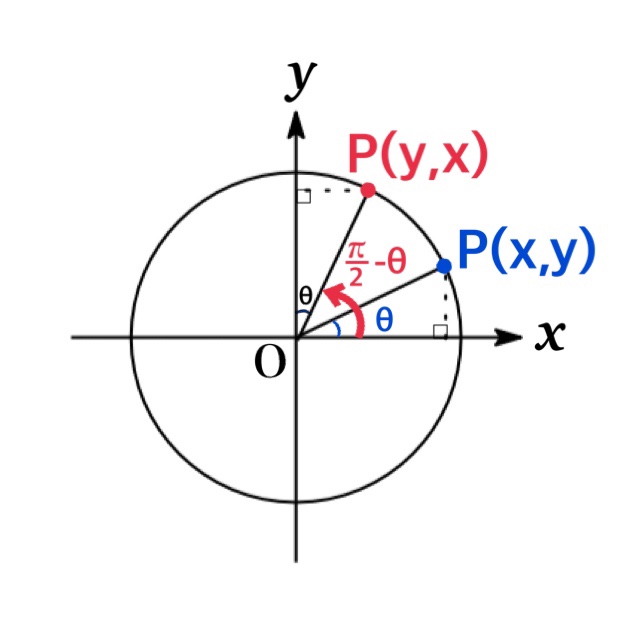
上式において $\theta$ を $-\theta$ で置き換えると, \begin{eqnarray*}\sin(90^{\circ}-\theta)&=&\cos (-\theta)=\cos \theta\\ \cos(90^{\circ}-\theta)&=&-\sin (-\theta)=\sin \theta\\\tan(90^{\circ}-\theta)&=&-\frac{1}{\tan (-\theta)}=\frac{1}{\tan \theta}\end{eqnarray*} を得る.
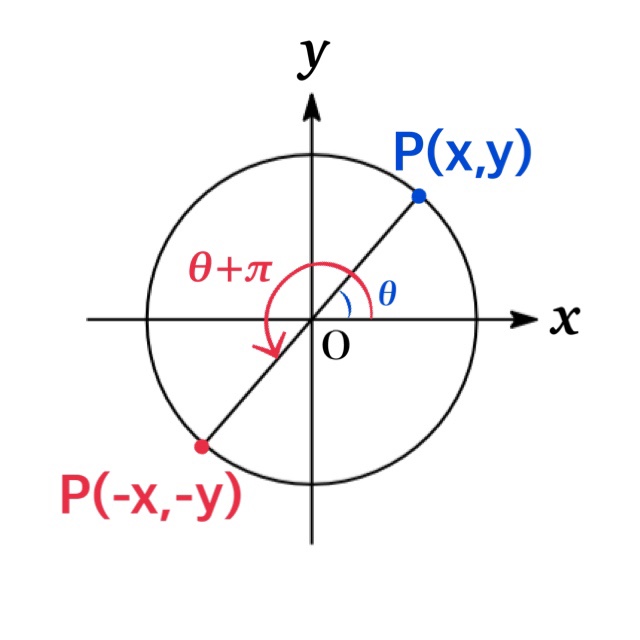
| ($\theta+\pi$)の三角関数 | |
| $\sin(180^{\circ}+\theta)=-\sin \theta$ | |
| $\cos(180^{\circ}+\theta)=-\cos \theta$ | |
| $\tan(180^{\circ}+\theta)=\tan \theta$ |
上式において $\theta$ を $-\theta$ で置き換えると\begin{eqnarray*}\sin(180^{\circ}-\theta)&=&-\sin (-\theta)=\sin \theta\\ \cos(180^{\circ}-\theta)&=&-\cos (-\theta)=-\cos \theta\\\tan(180^{\circ}-\theta)&=&\tan (-\theta)=-\tan\theta\end{eqnarray*} を得る.
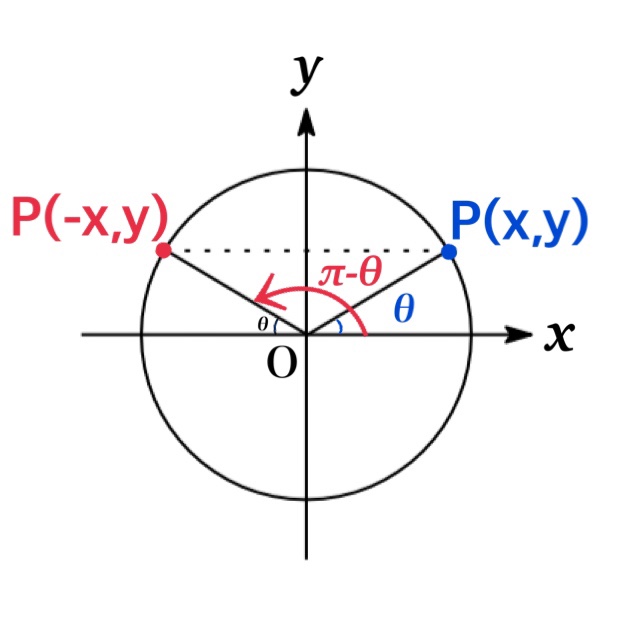
| ($\theta+2n\pi$)の三角関数 | |
| $\sin(360^{\circ}\times n +\theta)=\sin \theta$ | |
| $\cos(360^{\circ}\times n +\theta)=\cos \theta$ | |
| $\tan(360^{\circ}\times n +\theta)=\tan \theta$ |
加法定理
| $\sin (x+ y)=\sin x\cos y+ \cos x\sin y$ | |
| $\cos (x + y)=\cos x\cos y- \sin x\sin y$ | |
| $\tan (x + y)=\frac{\tan x+\tan y}{1-\tan x\tan y}$ |
上記の等式に y の代わりに -y を代入すれば, $\sin (x- y), \cos (x-y), \tan (x-y)$ の公式を得る.
2倍角の公式
| また上記の加法定理において y の代わりに x を代入すれば 2 倍角の公式を得る. → 詳細はこちら | |
| $\sin 2x=2\sin x\cos y$ | |
| $\cos 2x=\cos^{2} x- \sin^{2} x=1-2\sin^{2}x=2\cos^{2} x-1$ | |
| $\tan 2x=\frac{2\tan x}{1-\tan^{2} x}$ |
半角の公式
| 2倍角の公式より, $\cos 2x=1-2\sin^{2}x=2\cos^{2} x -1$ を変形すれば, $\sin^{2} x=\frac{1-\cos 2x}{2}, \cos^{2} x=\frac{1+\cos 2x}{2}$ を得る. これらの等式に $x$ に $\frac{x}{2}$ を代入すれば, 半角の公式を得る. →詳細はこちら | |
| $\sin^{2}\frac{x}{2}=\frac{1-\cos x}{2}$ | |
| $\cos^{2}\frac{x}{2}=\frac{1+\cos x}{2}$ | |
| $\tan^{2}\frac{x}{2}=\frac{1-\cos x}{1+\cos x}$ |
積と和の公式
「積から和」の公式は加法定理を用いて導くことができる. また「和から積」の公式は, 「積から和」の公式の変換により導かれる. → 詳細はこちら
| 和 → 積 | |
| $\sin A+\sin B=2\sin \frac{A+B}{2}\cos\frac{A-B}{2}$ | |
| $\sin A-\sin B=2\sin \frac{A-B}{2}\cos\frac{A+B}{2}$ | |
| $\cos A+\cos B=2\cos \frac{A+B}{2}\cos\frac{A-B}{2}$ | |
| $\cos A-\cos B=-2\sin \frac{A+B}{2}\sin\frac{A-B}{2}$ |
| 積 → 和 | |
| $2\sin A\cos B=\sin (A+B)+\sin (A-B)$ | |
| $2\cos A\sin B=\sin (A+B)-\sin (A-B)$ | |
| $2\cos A\cos B=\cos (A+B)+\cos (A-B)$ | |
| $2\sin A\sin B=-\{\cos (A+B)-\cos (A-B)\}$ |
合成
$A, \ B$ を定数とするとき, $A\sin \theta+B\cos \theta$ は次のように変形できる:
$$A\sin \theta+B\cos \theta=\sqrt{A^{2}+B^{2}}\sin (\theta +\alpha)$$
ただし $\cos \alpha=\frac{A}{\sqrt{A^{2}+B^{2}}}, \ \sin \alpha=\frac{B}{\sqrt{A^{2}+B^{2}}}$
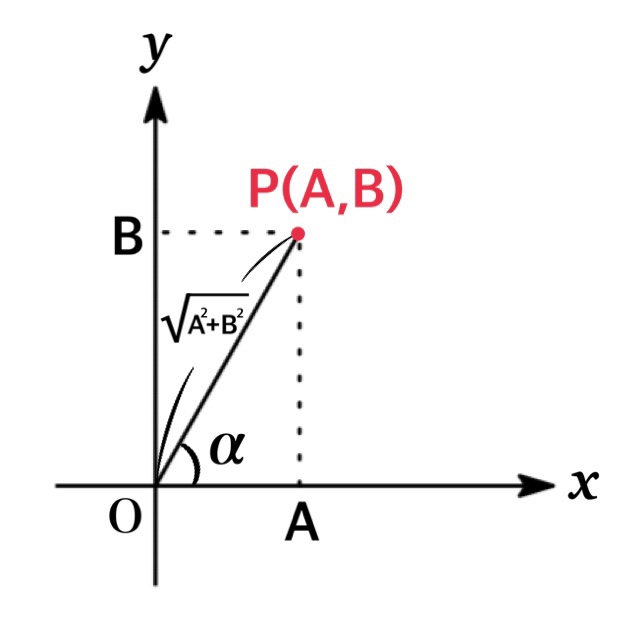
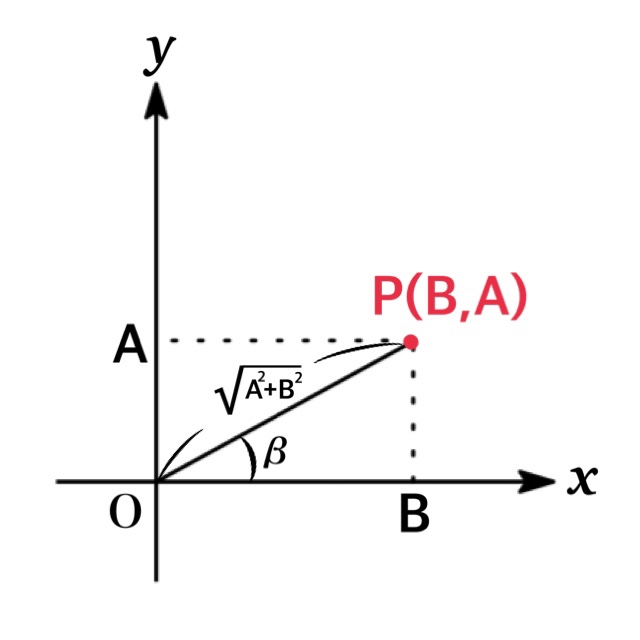
注意:三角関数の合成は $\sqrt{A^{2}+B^{2}}\cos (\theta -\beta)$ の形に変形することもできる.
$$A\sin \theta+B\cos \theta=\sqrt{A^{2}+B^{2}}\cos (\theta -\beta)$$
ただし $\sin \beta=\frac{A}{\sqrt{A^{2}+B^{2}}}, \ \cos \beta=\frac{B}{\sqrt{A^{2}+B^{2}}}$
導関数
| $(\sin x)’=\cos x$ | |
| $(\cos x)’=-\sin x$ | |
| $(\tan x)’=\frac{1}{\cos^{2} x}$ | |
| $(\mathrm{csc}\ x)’=-\mathrm{csc}\ x \cdot\mathrm{cot}\ x$ | |
| $(\mathrm{sec}\ x)’=\mathrm{sec}\ x \cdot\mathrm{tan}\ x$ | |
| $(\mathrm{cot}\ x)’=-\mathrm{csc}^{2}\ x$ |
積分
| $\int \sin x\ dx=-\cos x +C$ | |
| $\int \cos x\ dx=\sin x +C$ | |
| $\int \tan x\ dx=\ln |\sec x| +C$ | |
| $\int \csc x\ dx=\ln |\csc x-\cot x|+C$ | |
| $\int \sec x\ dx=\ln |\sec x+\tan x|+C$ | |
| $\int \cot x\ dx=\ln |\sin x|+C$ |