Let a>0 and \(a\not=1 \). Then, the inverse function of the exponential function \(f(x)=a^{x}\) is defined as the logarithmic function with base a. That is
$$\log_{a} x=y\ \ \ \ \Longleftrightarrow\ \ \ \ \ a^{y}=x$$
Notice that if a>0 and \(a\not=1 \), the exponential function \(f(x)=a^{x}\)is either increasing or decreasing. Thus, it is one-to-one and we can define the inverse function of it.
Example :
- \(\log_{2} 8=3 \) since \(2^{3}=8\).
- \(\log_{8} 2=\frac{1}{3}\) since \(8^{\frac{1}{3}}=2\).
- \(\log_{10} 0.01=-2 \) since \(10^{-2}=\frac{1}{10^{2}}=0.01\).
Contents
Properties
Let \(a>0\) and \(a\not= 1\).
| Properties | Example |
| \(\log_{a} 1=0\) | \(\log_{3} 1=0\) |
| \(\log_{a} a^{x}=x\) | \(\log_{2}8=\log_{2} 2^{3}=3\) |
| \(a^{\log_{a} x}=x\) | \(3^{\log_{3} 5}=5\) |
| \(\log_{a} (xy)=\log_{a}x+\log_{a}y\) | \(\log_{3} 35=\log_{3}5+\log_{3}7\) |
| \(\log_{a} \left(\frac{x}{y}\right)=\log_{a}x-\log_{a}y\) | \(\log_{3} \left(\frac{7}{5}\right)=\log_{3}7-\log_{3}5\) |
| \(\log_{a} x^{r}=r\log_{a}x\) | \(\log_{3} \sqrt{5}=\frac{1}{2}\log_{3}5\) |
| \(\log_{a} x=\frac{\log_{c}x}{\log_{c}a}\) | \(\log_{4} 9=\frac{\log_{2}9}{\log_{2}4}=\frac{1}{2}\log_{2}9=\log_{2}3\) |
| \(a^{\log_{b}c}=c^{\log_{b}a}\) | \(4^{\log_{2}3}=3^{\log_{2}4}=3^{2}=9\) |
| \((\log_{a} b)(\log_{b} c)=\log_{a}c\) | \((\log_{2} 3)(\log_{3} 5)=\log_{2}5\) |
| \(\log_{a^{n}} b=\frac{1}{n}\log_{a}b\) | \(\log _{8} 5=\log_{2^{3}} 5=\frac{1}{3}\log_{2} 5\) |
Graphs
| increase / decrease | comparison | |
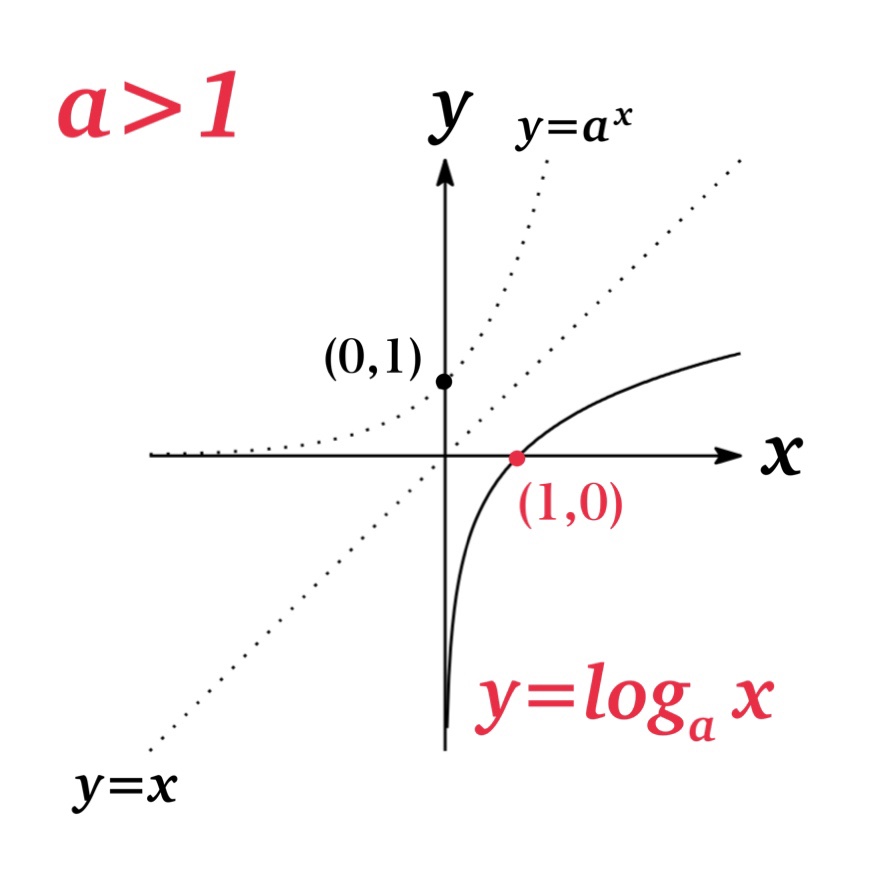
| a>1 (Fig.1) | \(f(x)=\log_{a} x\) is increasing. | \( 0< x_{1}< x_{2}\ \ \ \leftrightarrow\ \ \ \log_{a} x_{1}<\log_{a} x_{2}\) |
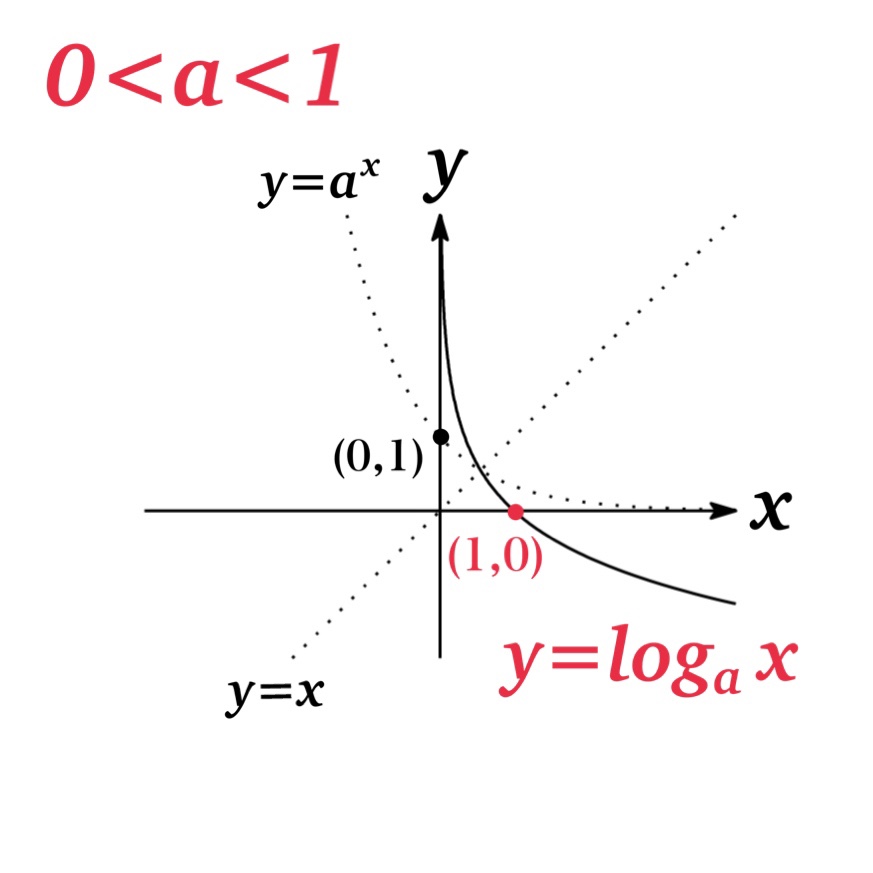
| 0<a<1 (Fig.2) | \(f(x)=\log_{a} x\) is decreasing. | \( 0< x_{1}< x_{2}\ \ \ \leftrightarrow\ \ \ \log_{a} x_{2}<\log_{a} x_{1}\) |
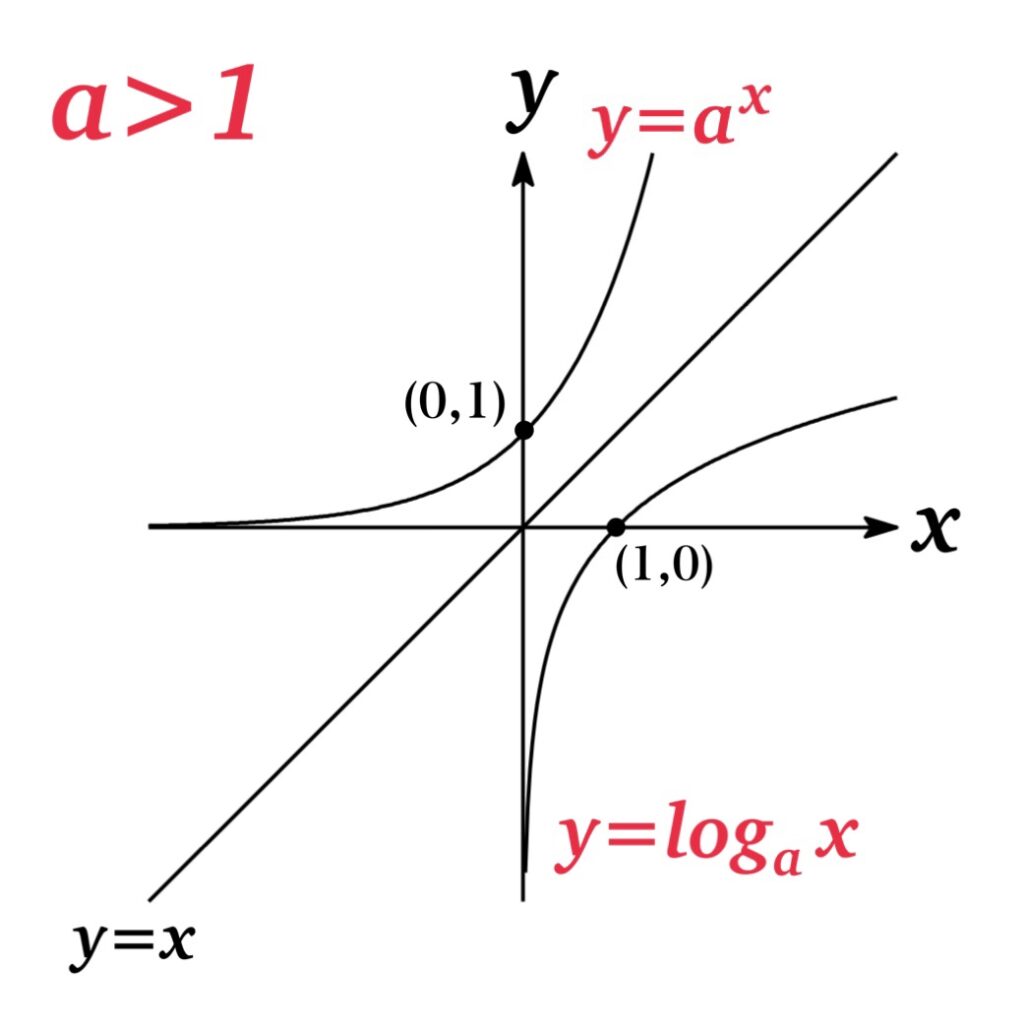
The graph of \(y=\log_{a} x\) is symmetric to \(y=a^{x}\) respect to \(y=x\) since properties of inverse functions.
Special case of \(a=10\) or \(\mathrm{e}\)
The logarithm with base \(\mathrm{e}\) is called the natural logarithm and has a special notation:
$$\log_{\mathrm{e}} x=\ln x$$
Similarly, the logarithm with base \(10\) is called the common logarithm and has a special notation:
$$\log_{\mathrm{10}} x=\log x$$
Notice that most text books in calculus use the notation the notation \(\ln x\) for the natural logarithm and \(\log x\) for the common logarithm. However, in the more advanced mathematical and scientific literature and in computer languages, the notation \(\log x\) is sometimes used for the natural logarithm.
Derivatives
We first see the derivatives of the natural logarithmic function :
$$\frac{d}{dx}\log_{\mathrm{e}} x=\frac{1}{x}\ \ \ \ \text{and}\ \ \ \ \ \frac{d}{dx} \log_{\mathrm{e}} f(x)=\frac{f'(x)}{f(x)}$$
This first equation is proven by differentiating \(\mathrm{e}^{y}=x\) implicitly with respect to x :
$$\mathrm{e}^{y} \frac{dy}{dx}=1$$
Thus we get
$$\frac{dy}{dx}=\frac{1}{\mathrm{e}^{y}}=\frac{1}{x}$$
and the second one is obtained by applying the Chain Rule to first equation.
$$\frac{d}{dx} \log_{a} x=\frac{1}{x\log_{e} a}$$
We use the fact that \(\log_{a} x=\frac{\log_{c}x}{\log_{c}a}\).
$$\frac{d}{dx}(\log_{a} x)=\frac{d}{dx}\left(\frac{\log_{\mathrm{e}}x}{\log_{\mathrm{e}}a}\right)=\frac{1}{\log_{\mathrm{e}}a}\frac{d}{dx}(\log_{\mathrm{e}}x)=\frac{1}{\log_{\mathrm{e}}a}\cdot \frac{1}{x}$$
Logarithmic Differentiation
The calculation of derivatives of complicated functions involving products, quotients, or powers can often be simplified by taking logarithms.
(Step 1)Take logarithms of both sides of an equation \(y=f(x)\).
(Step 2) Differentiate implicitly with respect to \(x\).
(Step 3)Solve the resulting equation for \(y’\).
Example: Differentiate \(y=\frac{x^{\frac{1}{3}}\sqrt{x^{2}+1}}{(3x+2)^{3}}\).
(Step1) Take logarithms of both sides of the equation and use properties of logarithms to simplify.
$$\ln y=\frac{1}{3}\ln x+\frac{1}{2}\ln (x^{2}+1)-3\ln (3x+2)$$
(Step 2) Differentiate implicitly with respect to x.
$$\frac{1}{y}\frac{dy}{dx}=\frac{1}{3}\cdot \frac{1}{x}+\frac{1}{2}\cdot \frac{2x}{x^{2}+1}-3\cdot\frac{3}{3x+2}$$
(Step 3) Solve for \(\frac{dy}{dx}\).
$$\begin{eqnarray*}\frac{dy}{dx}&=&y\left(\frac{1}{3x}+ \frac{x}{x^{2}+1}-\frac{9}{3x+2}\right)\\&=&\frac{x^{\frac{1}{3}}\sqrt{x^{2}+1}}{(3x+2)^{3}}\left(\frac{1}{3x}+ \frac{x}{x^{2}+1}-\frac{9}{3x+2}\right)\end{eqnarray*}$$