If \(\mathbf{a}\) and \(\mathbf{b}\) are nonzero vectors in either \(\mathbb{R}^{2}\) or \(\mathbb{R}^{3}\), there is a relationship between their inner product and the angle \(\theta\) between the two line segment from the origin to the points identified with \(\mathbf{a}\) and \(\mathbf{b}\).

---

Example : Find the angle between the vectors \(\mathbf{a}=(2, -1)^{t}, \ \mathbf{b}=(3,1)^{t}\).

Solution : Since \(|\mathbf{a}|=\sqrt{2^{2}+(-1)^{2}}=\sqrt{5} \ \ \ \ \text{and} \ \ \ \ \ |\mathbf{b}|=\sqrt{3^{2}+(1)^{2}}=\sqrt{10}\) and since \(\mathbf{a}\cdot \mathbf{b}=2\cdot 3 + (-1)\cdot 1 =5\), we have

$$\cos\theta=\frac{\mathbf{a}\cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|}=\frac{5}{\sqrt{5}\sqrt{10}}=\frac{1}{\sqrt{2}}$$

So the angle between \(\mathbf{a} \) and \(\mathbf{b} \) is \(\theta=\frac{\pi}{4}=45^{\circ}\).

---

Proof

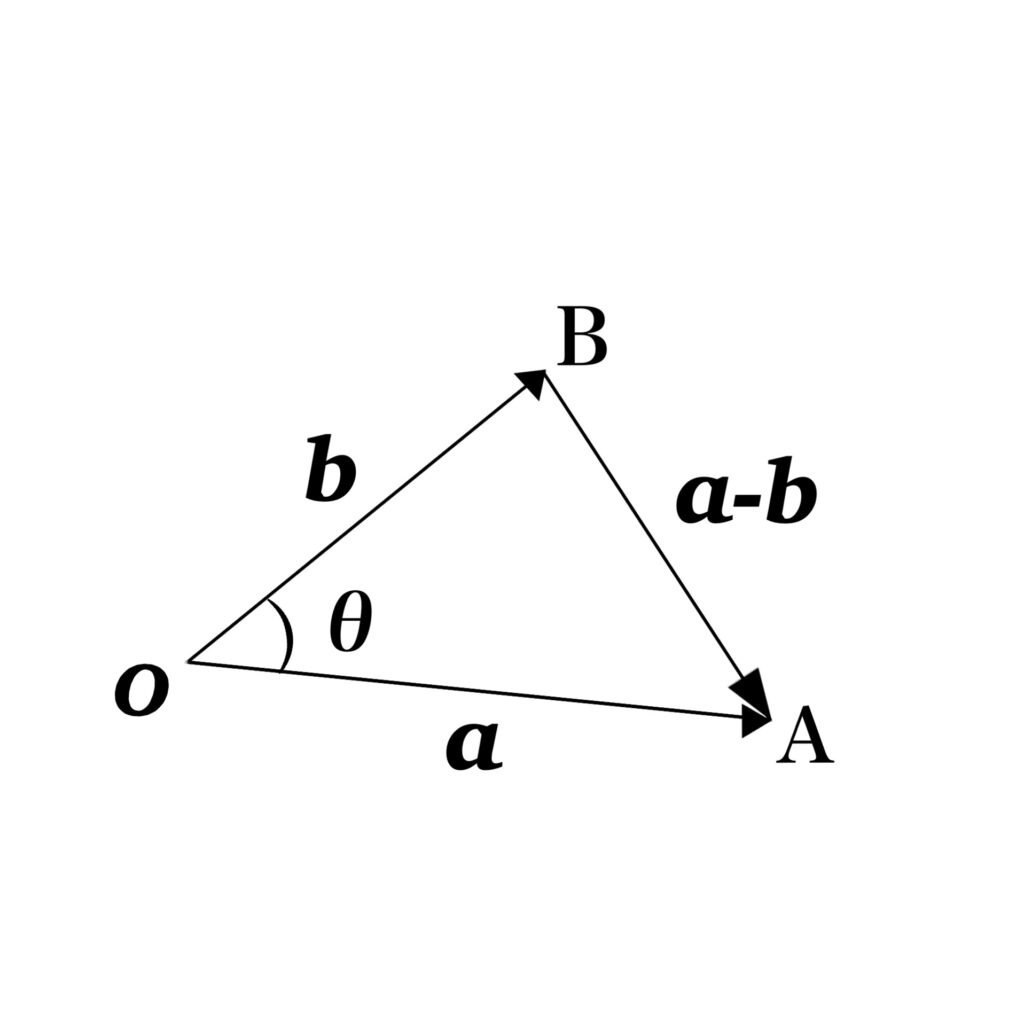
Then applying \(|OA|=|\mathbf{a}|,\ |OB|=|\mathbf{b}|,\ |AB|=|\mathbf{a}-\mathbf{b}|\), the above equation becomes

$$|\mathbf{a}-\mathbf{b}|^{2}=|\mathbf{a}|^{2}+|\mathbf{b}|^{2}-2|\mathbf{a}| |\mathbf{b}|\cos \theta\ \ \cdots \ (2)$$

Using the properties of the dot product, we can rewrite the LHS of (2) as follows:

$$\begin{eqnarray*}|\mathbf{a}-\mathbf{b}|^{2}&=&(\mathbf{a}-\mathbf{b})\cdot (\mathbf{a}-\mathbf{b})\\&=&\mathbf{a}\cdot \mathbf{a}-\mathbf{a}\cdot \mathbf{b}-\mathbf{b}\cdot \mathbf{a}+\mathbf{b}\cdot \mathbf{b}\\&=&|\mathbf{a}|^{2}-2\mathbf{a}\cdot \mathbf{b}+|\mathbf{b}|^{2}\end{eqnarray*}$$

Therefore, we have

$$|\mathbf{a}|^{2}-2\mathbf{a}\cdot \mathbf{b}+|\mathbf{b}|^{2}=|\mathbf{a}|^{2}+|\mathbf{b}|^{2}-2|\mathbf{a}| |\mathbf{b}|\cos \theta$$

Thus, we get

$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}| |\mathbf{b}|\cos\theta$$