$$\text{微分可能} \overset{\circ}{\underset{\times}{\rightleftharpoons}}\text{連続}$$
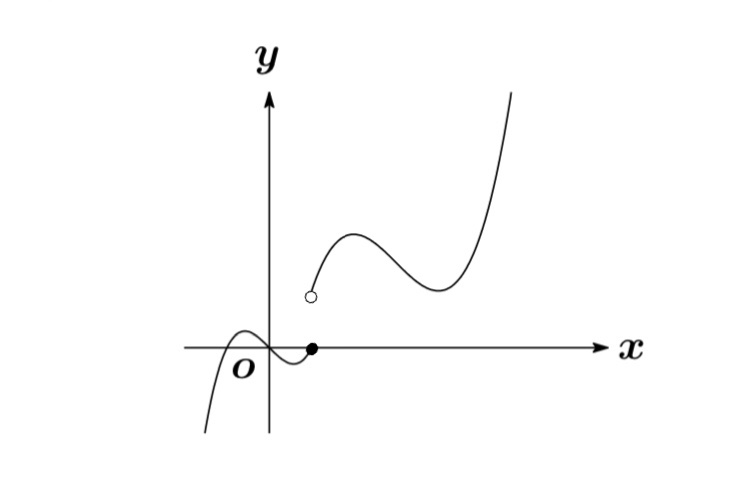
まずグラフが途中で途切れているような不連続な関数を考えてみよう.
不連続な点では明らかに微分可能でない.
すなわち「連続でないならば、微分可能ではない」がわかる.
よってこの主張の対偶として「微分可能なら連続である」が成り立つ.
しかし微分可能ならば連続であるが、その逆は常に成り立つわけではないので注意しよう.
Contents
微分可能⇒連続
関数 $f(x) $ が $x=a $で微分可能ならば、 $f(x)$ は $x=a$ で連続である.
証明 :
( 仮定 ) : $f(x)$ は $x=a$で微分可能である.
( 示すこと ): $\displaystyle\lim_{x\rightarrow a} f(x)$ が存在して, その値が $f(a)$ に等しい.
$f(x)$ が $x=a$ で微分可能であるので, $\displaystyle\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}=f'(a)$ が存在する. このとき
$$\begin{eqnarray*}\displaystyle\lim_{x\rightarrow a}\left(f(x)-f(a)\right)&=&\displaystyle\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}(x-a)\\&=&f'(a)\cdot 0\\&=&0\\&& \\\text{∴}\displaystyle\lim_{x\rightarrow a}f(x)&=&f(a)\end{eqnarray*}$$
連続⇏微分可能
関数 $f(x)$ が $x=a $で連続であっても、 $f(x)$ は $x=a$ で微分可能とは限らない.
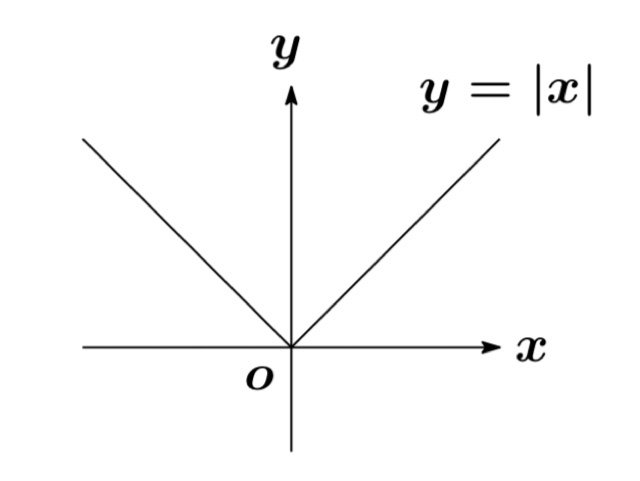
$y=|x|$ は $x=0$ で連続であるが、微分可能ではない.
連続性について
- $\displaystyle\lim_{x\rightarrow +0} |x|=0$
- $\displaystyle\lim_{x\rightarrow -0} |x|=0$
∴ $\displaystyle\lim_{x\rightarrow 0} |x|=0$
右極限と左極限の値が等しいことより、$x=0$ で $y=|x|$ は連続であることが示された.
微分可能性について
- $\displaystyle\lim_{x\rightarrow +0} \frac{|x|-0}{x-0}=\displaystyle\lim_{x\rightarrow +0} \frac{x}{x}=1$
- $\displaystyle\lim_{x\rightarrow -0} \frac{|x|-0}{x-0}=\displaystyle\lim_{x\rightarrow -0} \frac{-x}{x}=-1$
よって極限値 $f'(0)=\displaystyle\lim_{x\rightarrow 0} \frac{|x|-0}{x-0}$ は存在しないので, $y=|x|$ は $x=0$ で微分不可能である.