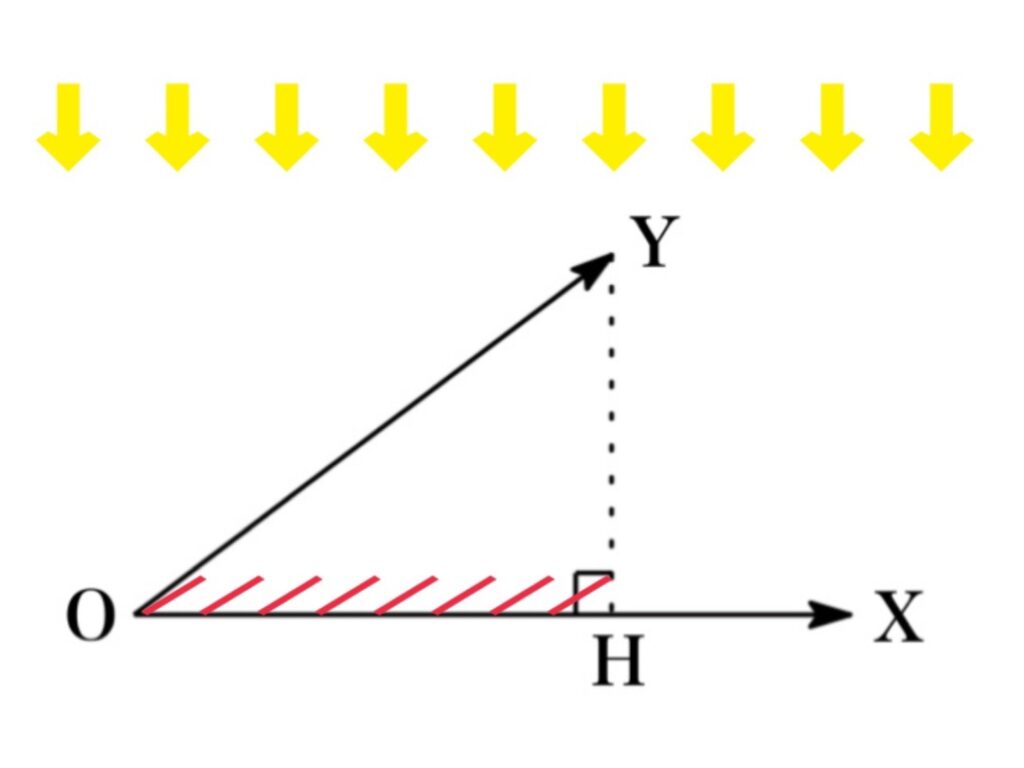
Let \(\overrightarrow{OX} \) and \(\overrightarrow{OY} \) be two vectors with the same initial point O. If H is the foot of the perpendicular from Y to the line containing OX , the vector with representation \(\overrightarrow{OH} \) is called the vector projection of \(\overrightarrow{OY} \) onto \(\overrightarrow{OX} \) is denoted by $\text{proj}{}_{x}\mathbf{y}$ and is geiven by
$$\text{proj}_{x}\mathbf{y}=\overrightarrow{OH}=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|^{2}}\overrightarrow{OX}$$

Significance of Projections
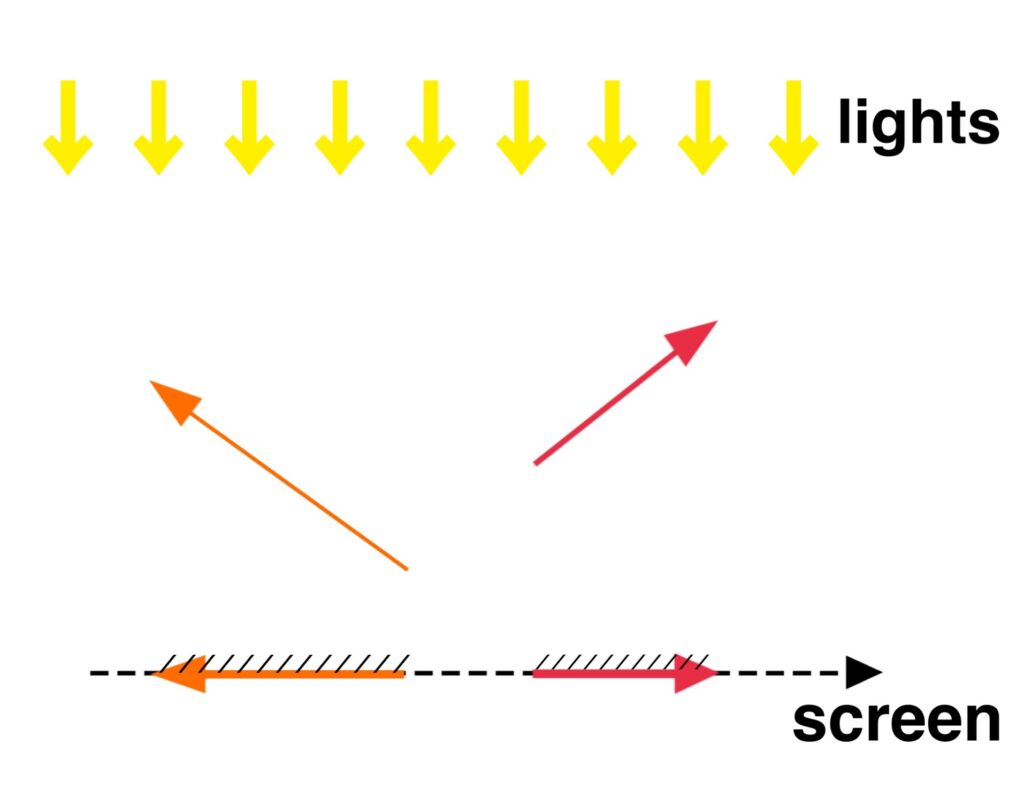
The image created when a light is shined on an object is called projection. Especially, the projection by light rays perpendicular to the screen is called normal projection.

Example
Find the vector projection of y=(1,1,2) onto x=(-2,3,1).
Since $|\mathbf{x}|=\sqrt{(-2)^{2}+3^{2}+1^{2}}=\sqrt{14}$ and $\mathbf{x}\cdot \mathbf{y}=(-2)\cdot 1+3\cdot 1+1\cdot 2=3$, the vector projection is given by
$$\text{proj}_{\mathbf{x}}\mathbf{y}=\frac{\mathbf{x}\cdot \mathbf{y}}{|\mathbf{x}|^{2}}\mathbf{x}=\frac{3}{14}(-2,3,1)=\left(-\frac{3}{7},\frac{9}{14},\frac{3}{14}\right)$$
Proof
Proof (1)
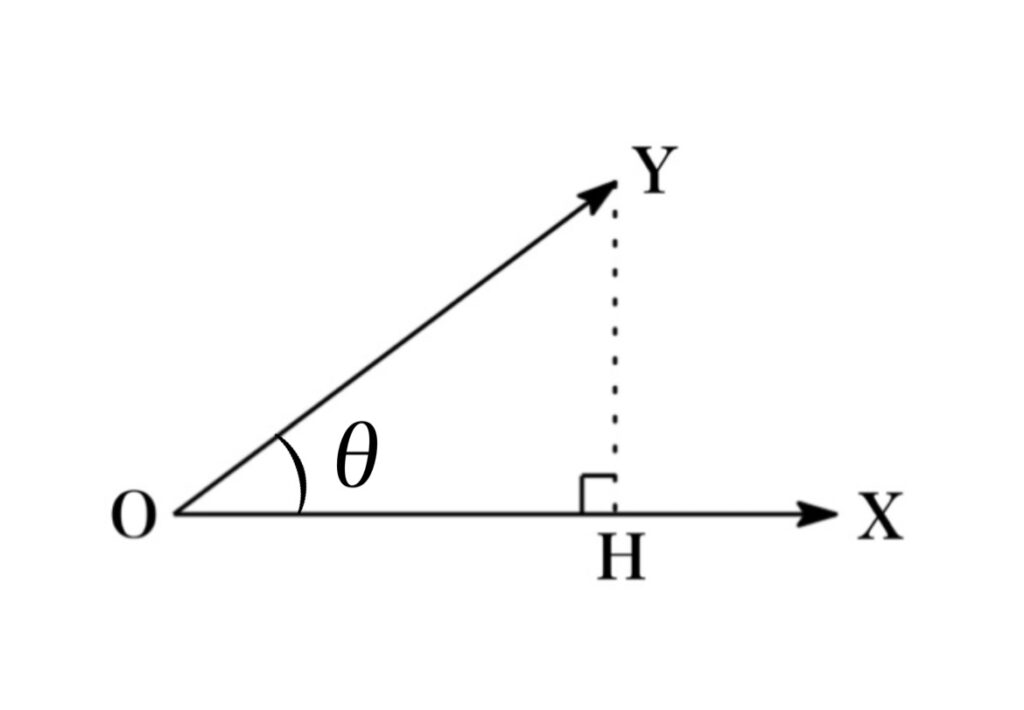
Let \(\theta\) be the angle between \(\overrightarrow{OX}\) and \(\overrightarrow{OY}\). Then from definition of the dot products, we have
$$\overrightarrow{OX}\cdot \overrightarrow{OY}=|\overrightarrow{OX}| |\overrightarrow{OY}|\cos\theta =|\overrightarrow{OX}||\overrightarrow{OH}|$$
Therefore the schalr projection of \(\overrightarrow{OY} \) onto \(\overrightarrow{OX} \) is given by $$|\overrightarrow{OH}|=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|}$$
The vector projection is the scalar projection times the unit vector in the direction of $\overrightarrow{OX}$, thus we obtain
$$\overrightarrow{OH}=|\overrightarrow{OH}|\times \frac{\overrightarrow{OX}}{|\overrightarrow{OX}|}=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|}\times \frac{\overrightarrow{OX}}{|\overrightarrow{OX}|}=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|^{2}}\overrightarrow{OX}$$
Proof(2)
Let r be a real number, and then \(\overrightarrow{OH}\) can be written as
$$\overrightarrow{OH}=r\ \overrightarrow{OX}$$
Since YH is perpendicular to the line contating OX, we have $$\overrightarrow{YH}\cdot \overrightarrow{OX}=0$$
Then
$$\begin{eqnarray*}\overrightarrow{YH}\cdot \overrightarrow{OX}&=&(\overrightarrow{OH}-\overrightarrow{OY})\cdot \overrightarrow{OX}\\&=&(r\ \overrightarrow{OX}-\overrightarrow{OY})\cdot \overrightarrow{OX}\\&=&r|\overrightarrow{OX}|^{2}-\overrightarrow{OX}\cdot\overrightarrow{OY}\\&=&0\end{eqnarray*}$$
Thus,
$$r=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|^{2}}$$
Therefore we obtain
$$\overrightarrow{OH}=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|^{2}}\overrightarrow{OX}$$