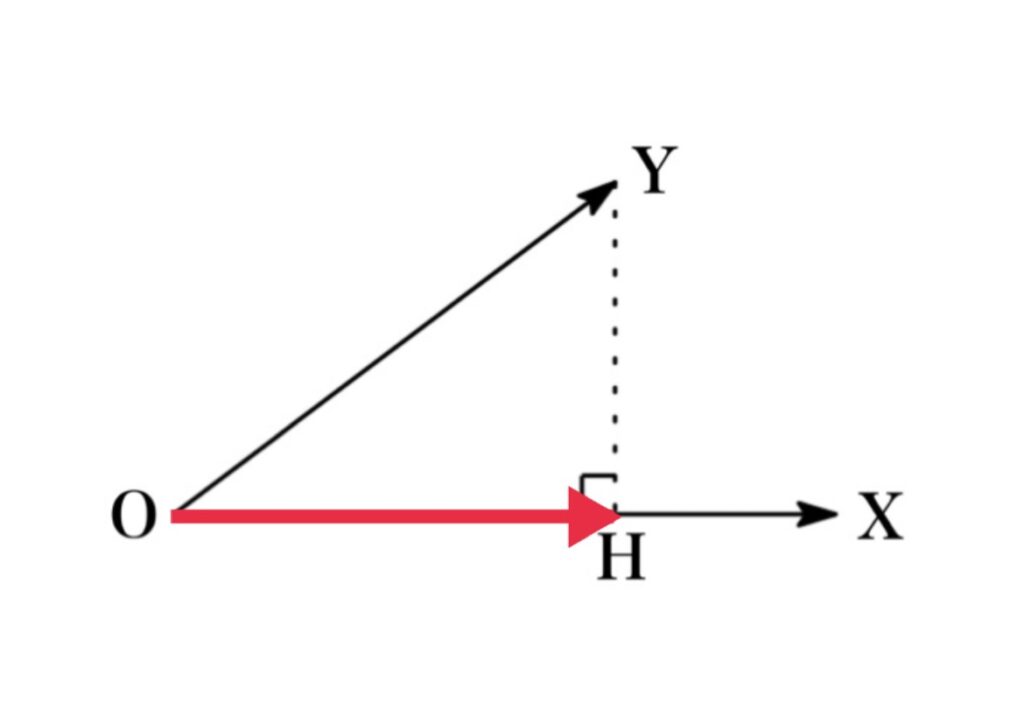
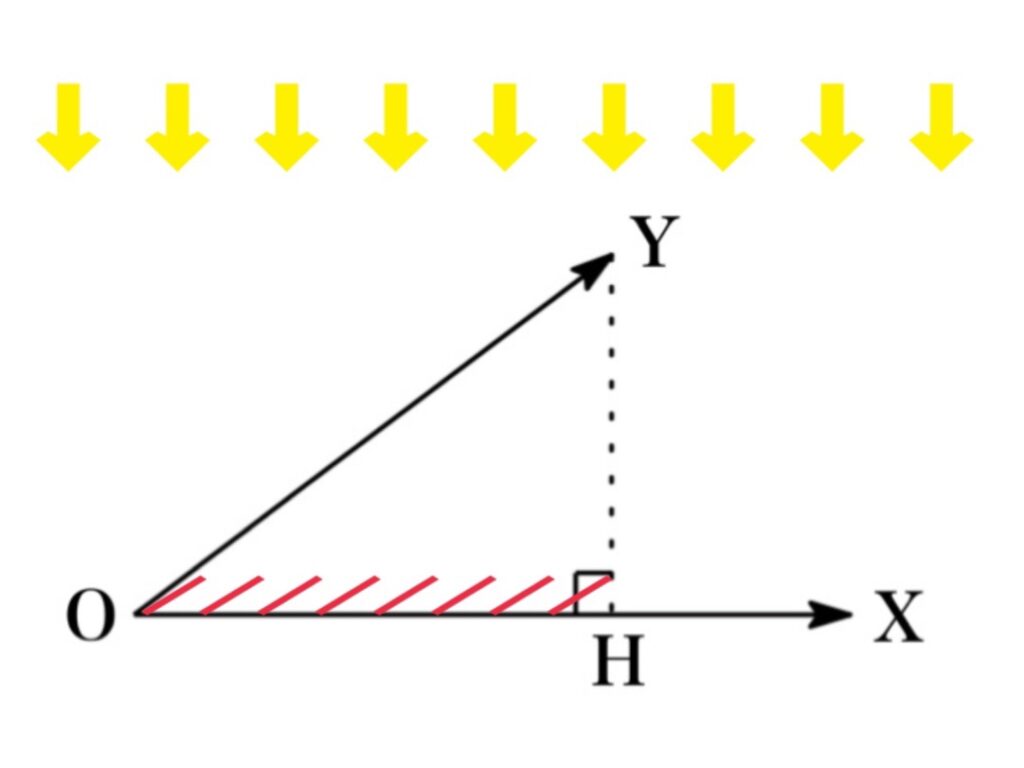
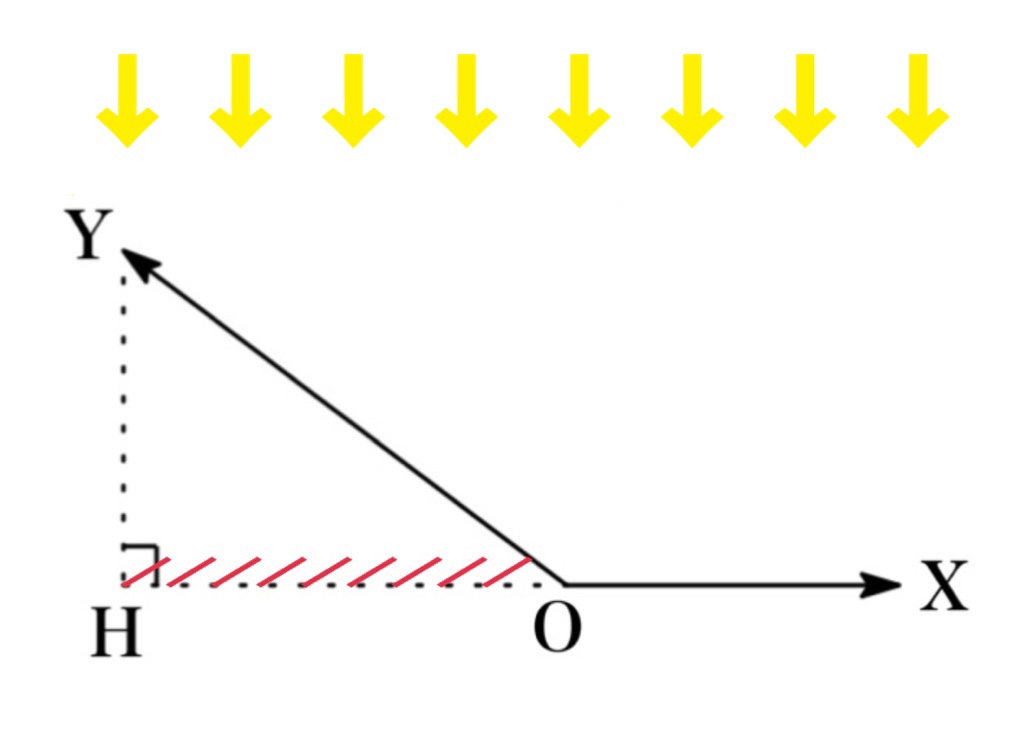
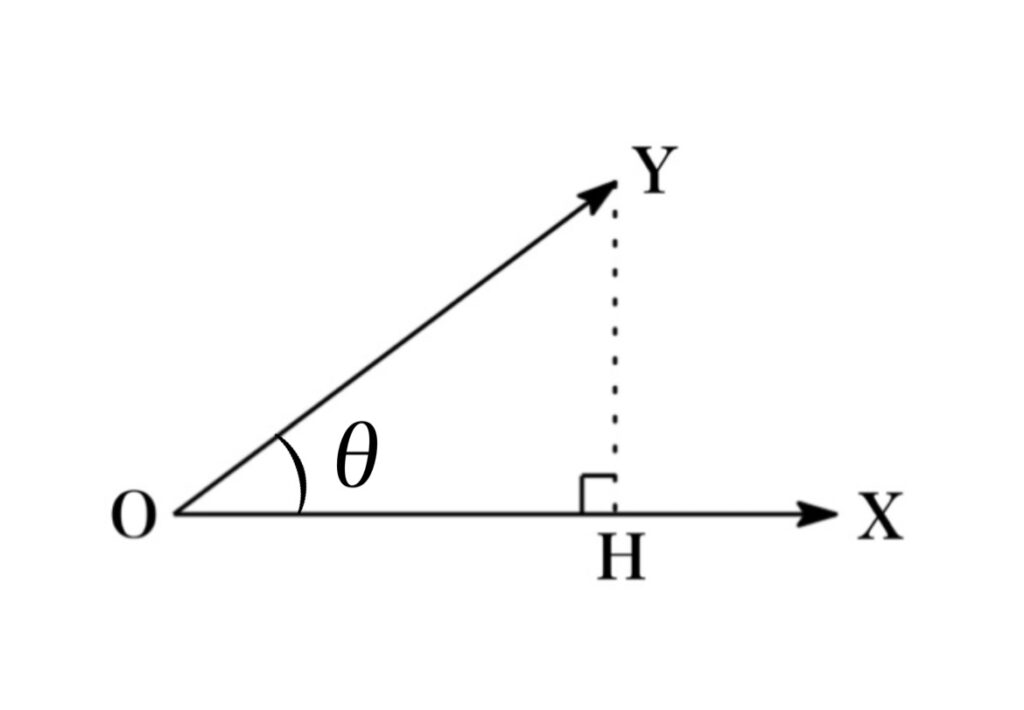
正射影ベクトル \(\overrightarrow{OH}\)とは, ベクトル \(\overrightarrow{OY}\) に対して上から光を当てた時にスクリーン \(\overrightarrow{OX}\) 上に映し出される影となるベクトルのことである.
例
$\mathbf{x}=(-2,3,1)$, $\mathbf{y}=(1,1,2)$ とするとき, $\mathbf{y}$ の $\mathbf{x}$ への正射影ベクトルを求めよ.
$|\mathbf{x}|=\sqrt{(-2)^{2}+3^{2}+1^{2}}=\sqrt{14}$, $\mathbf{x}\cdot \mathbf{y}=(-2)\cdot 1+3\cdot 1+1\cdot 2=3$より, $\mathbf{y}$ の $\mathbf{x}$ への正射影ベクトルは次で与えられる:
$$\text{proj}_{\mathbf{x}}\mathbf{y}=\frac{\mathbf{x}\cdot \mathbf{y}}{|\mathbf{x}|^{2}}\mathbf{x}=\frac{3}{14}(-2,3,1)=\left(-\frac{3}{7},\frac{9}{14},\frac{3}{14}\right)$$
証明
証明(1)
$\overrightarrow{OY}$ と $\overrightarrow{OY}$ のなす各を $\theta$ とする. このとき内積の定義より
$$\overrightarrow{OX}\cdot \overrightarrow{OY}=|\overrightarrow{OX}| |\overrightarrow{OY}|\cos\theta =|\overrightarrow{OX}||\overrightarrow{OH}|$$
よって $|\overrightarrow{OH}|$ は次で表される:
$$|\overrightarrow{OH}|=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|}$$
また正射影ベクトル $\overrightarrow{OH}$は $|\overrightarrow{OH}|$ に$\overrightarrow{OX}$ 方向の大きさ $1$ の単位ベクトルをかけたものなので
$$\overrightarrow{OH}=|\overrightarrow{OH}|\times \frac{\overrightarrow{OX}}{|\overrightarrow{OX}|}=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|}\times \frac{\overrightarrow{OX}}{|\overrightarrow{OX}|}=\frac{\overrightarrow{OX}\cdot \overrightarrow{OY}}{|\overrightarrow{OX}|^{2}}\overrightarrow{OX}$$
証明(2)
実数 \(r\) を用いて \(\overrightarrow{OH}=r\ \overrightarrow{x}\)とおく.
このとき条件より \(\overrightarrow{YH}\cdot \overrightarrow{x}=0\) であるから
$$(\overrightarrow{OH}-\overrightarrow{OY})\cdot \overrightarrow{x}=0$$
$$\text{∴}\ (r\ \overrightarrow{x}-\overrightarrow{y})\cdot \overrightarrow{x}=0$$
よって$$r|\overrightarrow{x}|^{2}-\overrightarrow{x}\cdot\overrightarrow{y}=0$$
$$\text{∴}\ r=\frac{\overrightarrow{x}\cdot \overrightarrow{y}}{|\overrightarrow{x}|^{2}}$$
すなわち$$\overrightarrow{OH}=\frac{\overrightarrow{x}\cdot \overrightarrow{y}}{|\overrightarrow{x}|^{2}}\overrightarrow{x}$$