Let $A$ and $B$ be constants. Then $A\sin \theta+B\cos \theta$ can be transformed as below:
$$A\sin \theta+B\cos \theta=\sqrt{A^{2}+B^{2}}\sin (\theta +\alpha)$$
where $\cos \alpha=\frac{A}{\sqrt{A^{2}+B^{2}}}$ and $\sin \alpha=\frac{B}{\sqrt{A^{2}+B^{2}}}$
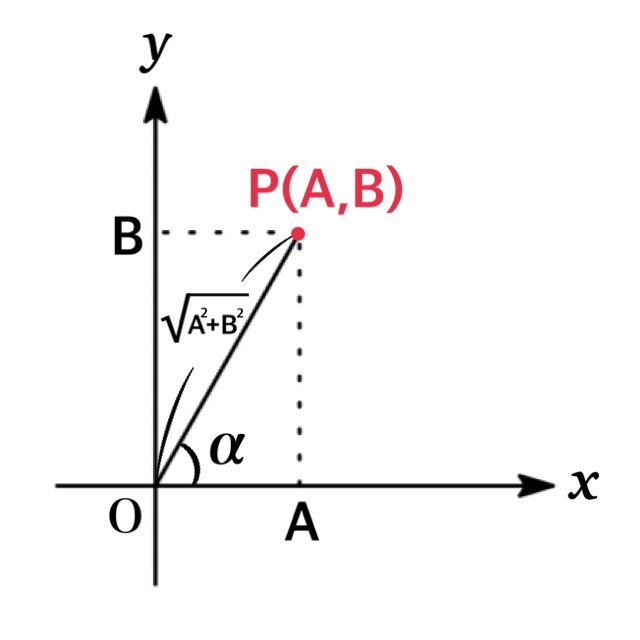
Suppose that the constants $A$ and $B$ are given. Then, if we take the point $P(A,B)$ on the $xy$ plane, we have
$$OP=\sqrt{A^{2}+B^{2}}$$
Also let $\alpha$ be the angle between the positive $x$-axis and $OP$ obtained by counterclockwise rotation. Then we get
$$A=\sqrt{A^{2}+B^{2}}\cdot \cos\alpha,\ \ \ B=\sqrt{A^{2}+B^{2}}\cdot \sin\alpha$$
Therefore, we obtain
\begin{eqnarray*}A\sin \theta+B\cos \theta&=&\sqrt{A^{2}+B^{2}}\cdot \cos\alpha\sin\theta+\sqrt{A^{2}+B^{2}}\cdot \sin\alpha\cos\theta\\&=&\sqrt{A^{2}+B^{2}}(\sin\theta\cos\alpha+\cos\theta\sin\alpha)\\&=&\sqrt{A^{2}+B^{2}}\sin (\theta +\alpha)\end{eqnarray*}
NOTE:If $A$ and $B$ are constants, the function $y=A\sin\theta+B\cos\theta$ can be transformed as $y=\sqrt{A^{2}+B^{2}}\sin (\theta +\alpha)$, its maximum value is given by $\sqrt{A^{2}+B^{2}}$ and its minimum value is given by $-\sqrt{A^{2}+B^{2}}$.
Contents
Example
Transform $\sin\theta+\sqrt{3}\cos\theta$ into the form $r\sin(\theta+\alpha)$.
Since $A = ($the coefficient of $\sin\theta)=1$, $B=($ the coefficient of $\cos\theta)=\sqrt{3}$ , we have
$$\sqrt{A^{2}+B^{2}}=\sqrt{1^{2}+(\sqrt{3})^{2}}=2$$
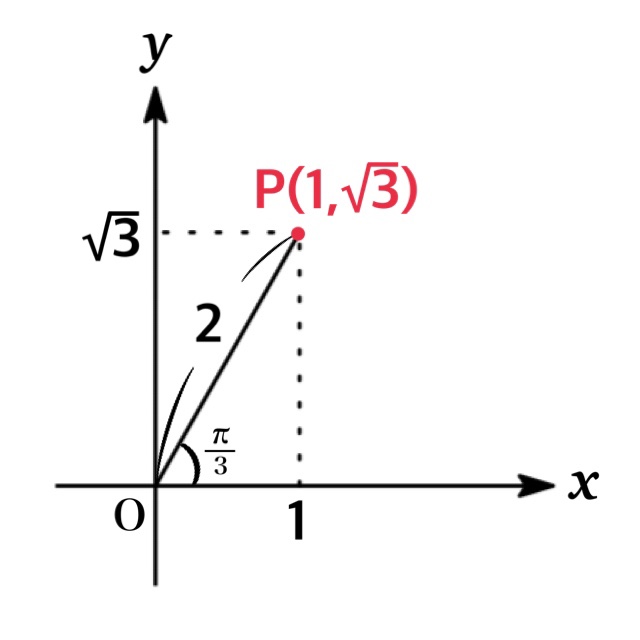
Also if we take the point $P(1,\ \sqrt{3})$, the angle between the positive $x$-axis and $OP$ obtained by counterclockwise rotation is given $\alpha=\frac{\pi}{3}$. Thus, we obtain
$$y=\sin\theta+\sqrt{3}\cos\theta=2\sin(\theta+\frac{\pi}{3})$$
Remark
$A\sin \theta+B\cos \theta$ can be also transformed into the form $\sqrt{A^{2}+B^{2}}\cos (\theta -\beta)$ :
Let $A$ and $B$ be constants. Then
$$A\sin\theta +B\cos \theta=\sqrt{A^{2}+B^{2}}\cos (\theta -\beta)$$
where $\sin \beta=\frac{A}{\sqrt{A^{2}+B^{2}}}$ and $\cos \beta=\frac{B}{\sqrt{A^{2}+B^{2}}}$
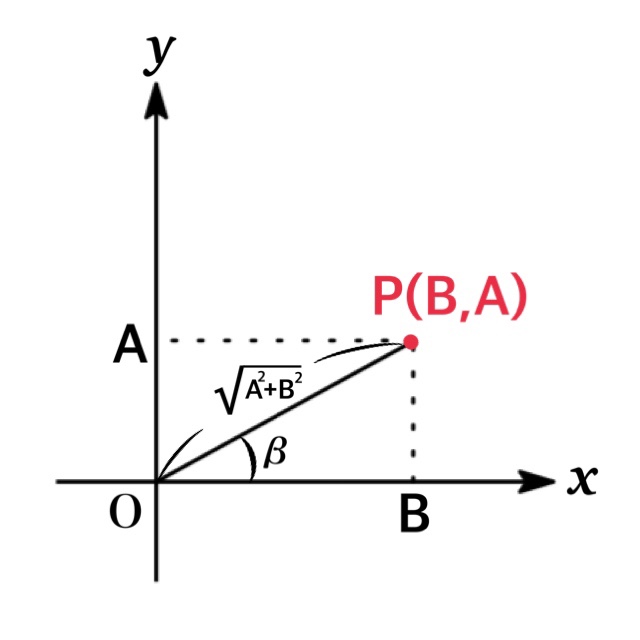
In this case we take the point $P(B,A)$ as shown in Fig and let $\beta$ be the angle between the positive $x$-axis and $OP$ obtained by counterclockwise rotation. Then we get
$$A=\sqrt{A^{2}+B^{2}}\cdot \sin\beta,\ \ \ B=\sqrt{A^{2}+B^{2}}\cdot \cos\beta$$
Therefore, we obtain
\begin{eqnarray*}A\sin \theta+B\cos \theta&=&\sqrt{A^{2}+B^{2}}\cdot \sin\beta\sin\theta+\sqrt{A^{2}+B^{2}}\cdot \cos\beta\cos\theta\\&=&\sqrt{A^{2}+B^{2}}(\sin\theta\sin\beta+\cos\theta\cos\beta)\\&=&\sqrt{A^{2}+B^{2}}\cos (\theta -\beta)\end{eqnarray*}
Example
Transform $\sin\theta+\sqrt{3}\cos\theta$ into the form $r\cos(\theta-\beta)$.
Since $A =1$, $B=\sqrt{3}$, we have
$$\sqrt{A^{2}+B^{2}}=\sqrt{1^{2}+(\sqrt{3})^{2}}=2$$
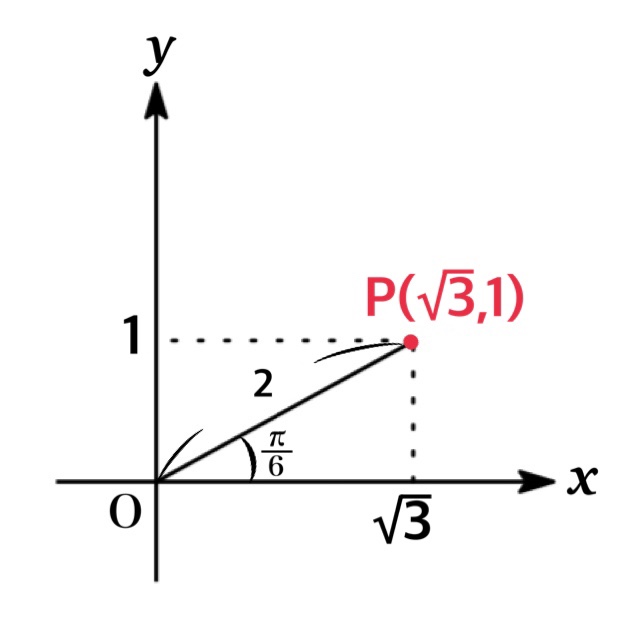
Also if we take the point $P(\sqrt{3},\ 1)$, the angle between the positive $x$-axis and $OP$ obtained by counterclockwise rotation is given $\beta=\frac{\pi}{6}$. Thus, we obtain
$$y=\sin\theta+\sqrt{3}\cos\theta=2\cos(\theta-\frac{\pi}{6})$$