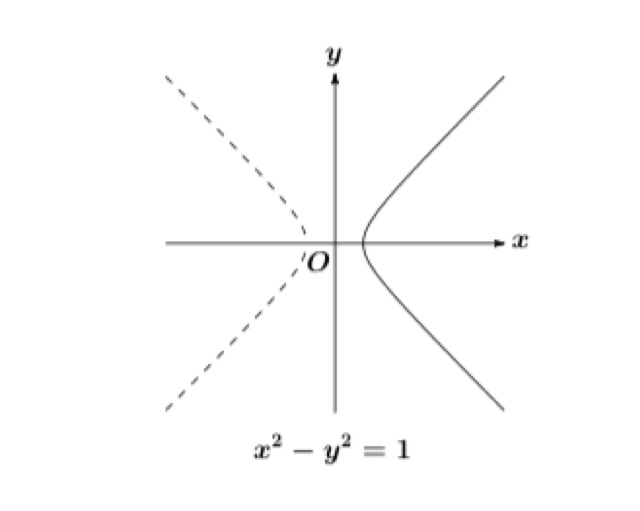
Plot the point \((x,y)=(\cosh t, \sinh t)\), and consider why it is called a “hyperbolic” functions.
Let \(x=\cosh t\) and \(y=\sinh t\).
Then the point \((x,y)=(\cosh t, \sinh t)\) lies on the right branch of the hyperbola \(x^{2}-y^{2}=1\) since \(\cosh^{2} t-\sinh^{2} t=1\) and \(\cosh t\geq 1\).
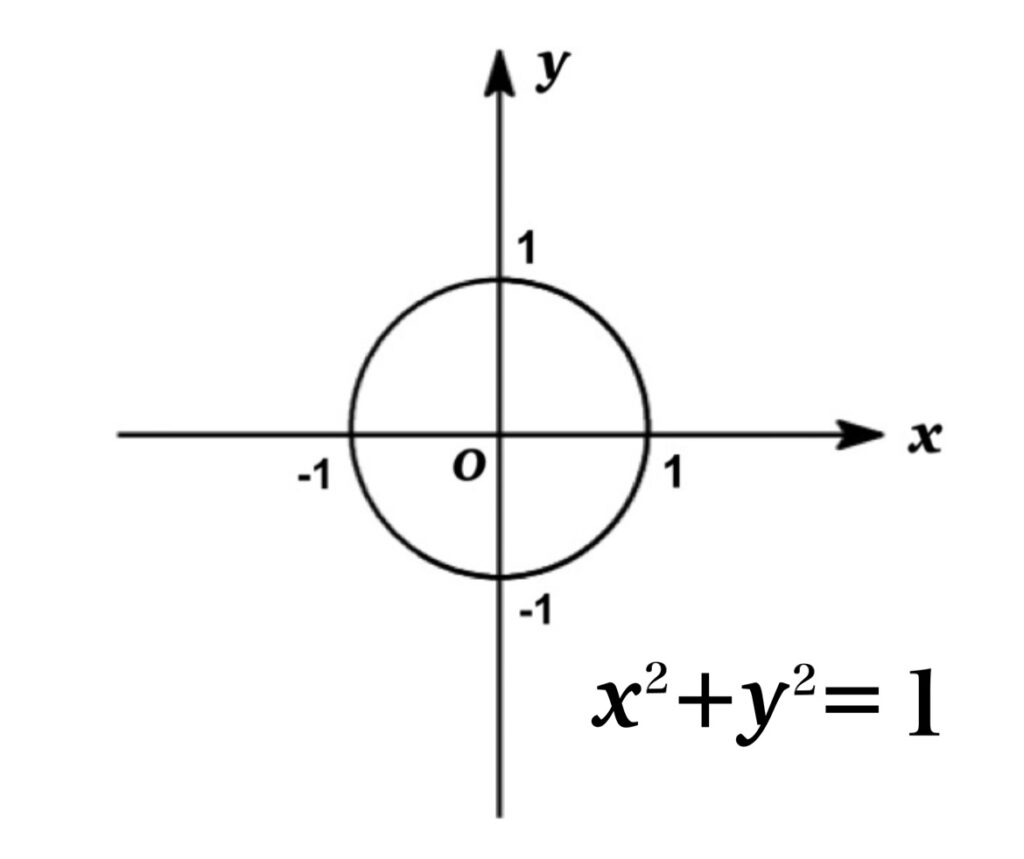
For your reference, recall that trigonometric functions have similar properties.
Likewise, the point \((x,y)=(\cos t, \sin t)\) lies on the unit circle \(x^{2}+y^{2}=1\) since \(\cos^{2} t+\sinh^{2} t=1\).