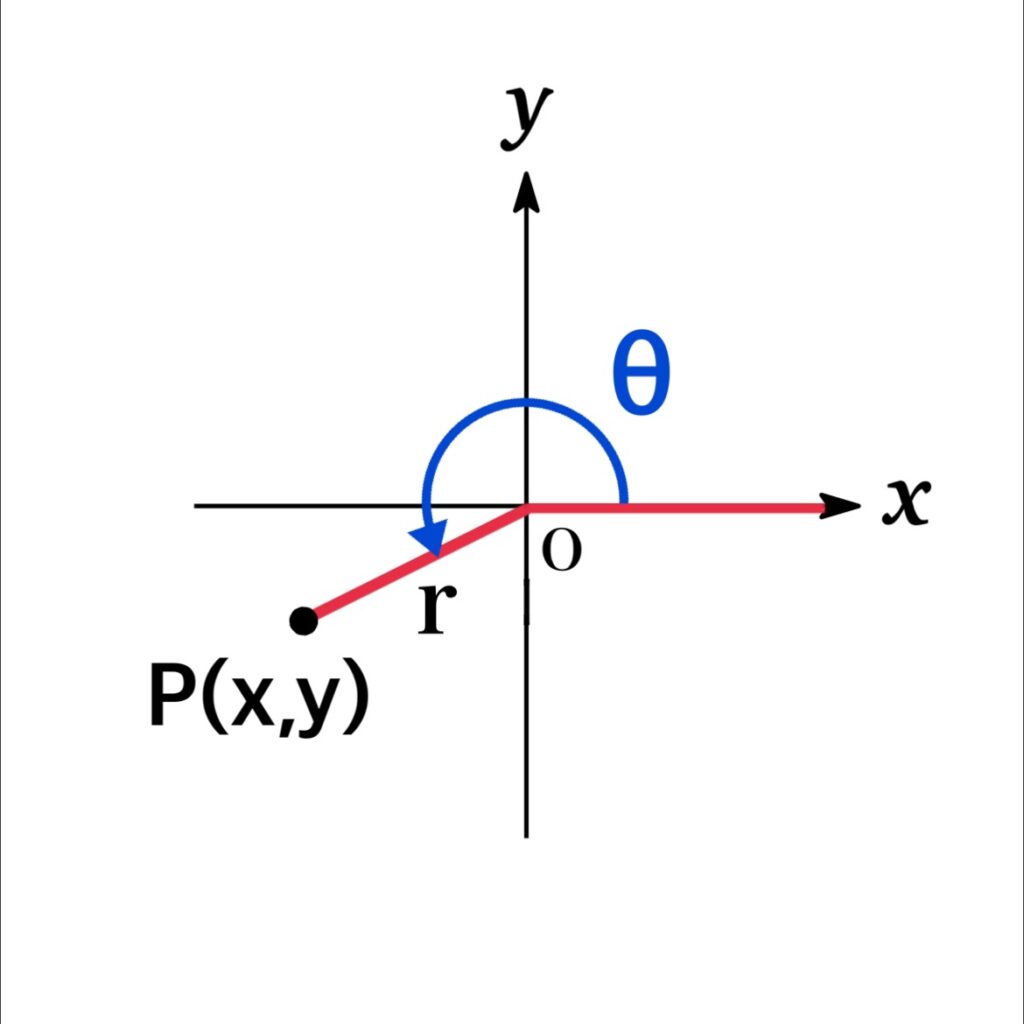
Consider any point $P(x,y)$ on $xy$ plane. Now, we let $r$ be the distance $|OP|$ and $\theta$ be the angle between the positive $x$-axis and $OP$ obtained by counterclockwise rotation as shown in Fig. Then we define trigonometric functions as below:
$$\sin \theta=\frac{y}{r},\ \ \ \cos \theta=\frac{x}{r}, \ \ \ \tan \theta=\frac{y}{x}$$
Furthermore, the others’ functions are also defined.
$$\mathrm{csc}\ x=\frac{1}{\sin x}, \ \ \ \mathrm{sec}\ x=\frac{1}{\cos x},\ \ \ \mathrm{cot}\ x=\frac{1}{\tan x}$$
Contents
Identities
| $\tan x=\frac{\sin x}{\cos x}$ | |
| $\sin^{2} x+\cos^{2} x=1$ | |
| $1+\tan^{2} x=\frac{1}{\cos^{2} x}$ |
Graphs
| Period | Symmetry | |
| $y=\sin \theta$ | $360^{\circ}$ | Origin |
| $y=\cos \theta$ | $360^{\circ}$ | y-axis |
| $y=\tan \theta$ | $180^{\circ}$ | Origin |
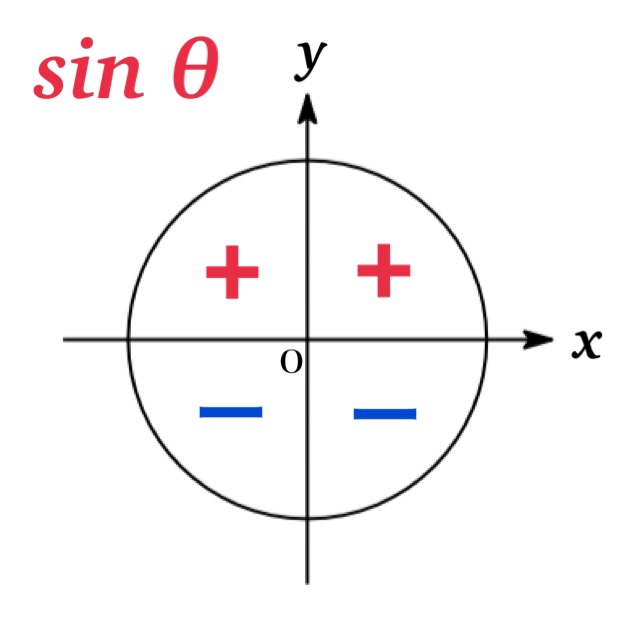
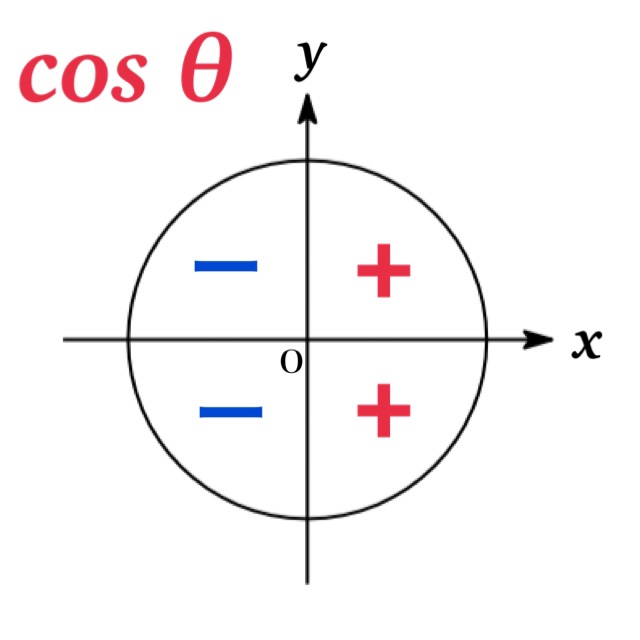
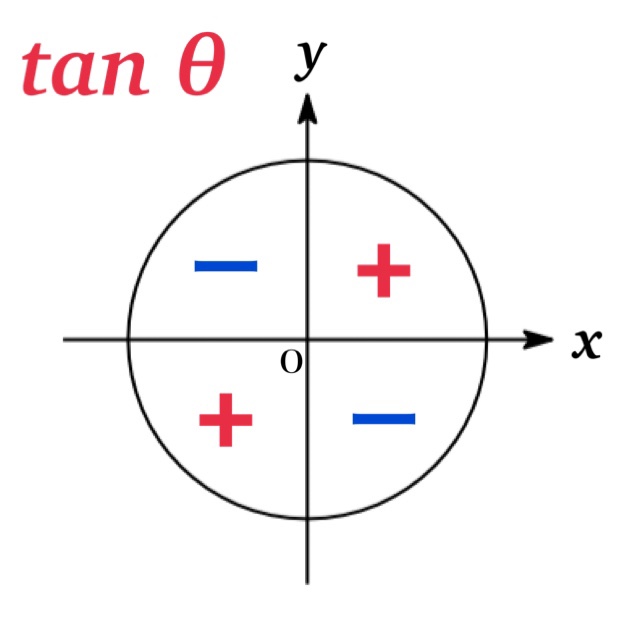
Signs
The signs of the trigonometric functions depend on angles in each of the four quadrants. For example, if $0\leq \theta\leq 180^{\circ}$, the sign of $\sin \theta$ is $+$ since $0 \leq\sin \theta\leq 1$.
Even and Odd functions
| $\sin (-x)=-\sin x$ | Odd (Origin symmetry) |
| $\cos (-x)=\cos x$ | Even(y-axis symmetry) |
| $\tan (-x)=-\tan x$ | Odd(Origin symmetry) |
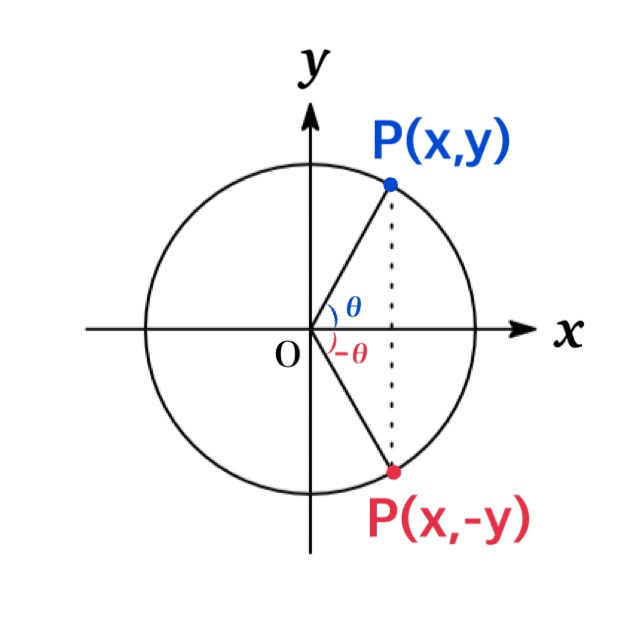
That \(\sin x\) is an odd function and \(\cos x\) is an even function are easily proved drawing a diagram showing \(\theta\) and \(-\theta\)
Angle of $(90^{\circ}\times m)+\theta$
| Angle of ($\theta+\frac{\pi}{2}$) | |
| $\sin(90^{\circ}+\theta)=\cos \theta$ | |
| $\cos(90^{\circ}+\theta)=-\sin \theta$ | |
| $\tan(90^{\circ}+\theta)=-\frac{1}{\tan \theta}$ |
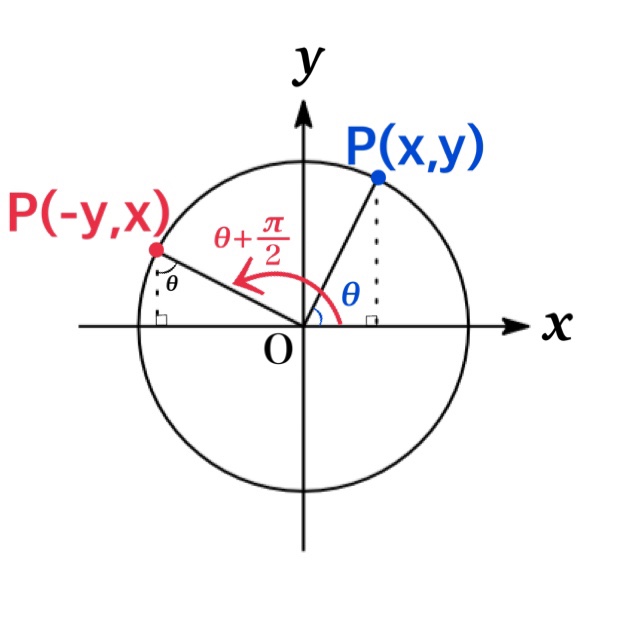
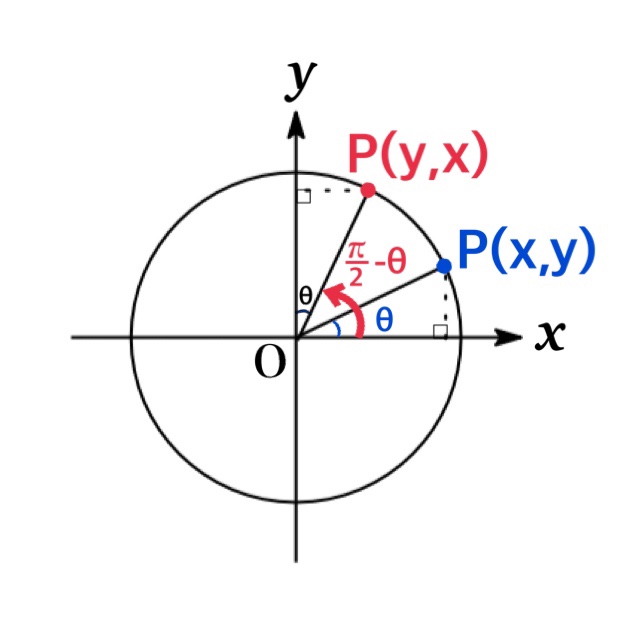
By substituting $-\theta$ for $\theta$ in above equations, we obtain \begin{eqnarray*}\sin(90^{\circ}-\theta)&=&\cos (-\theta)=\cos \theta\\ \cos(90^{\circ}-\theta)&=&-\sin (-\theta)=\sin \theta\\\tan(90^{\circ}-\theta)&=&-\frac{1}{\tan (-\theta)}=\frac{1}{\tan \theta}\end{eqnarray*}
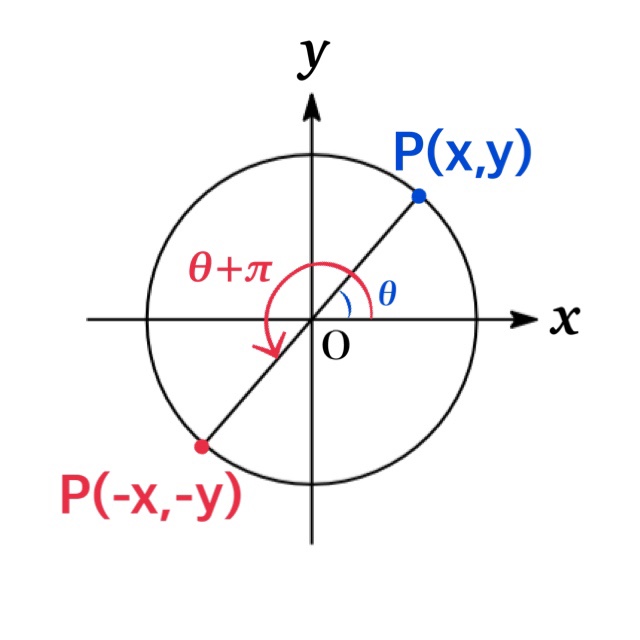
| Angle of ($\theta+\pi$) | |
| $\sin(180^{\circ}+\theta)=-\sin \theta$ | |
| $\cos(180^{\circ}+\theta)=-\cos \theta$ | |
| $\tan(180^{\circ}+\theta)=\tan \theta$ |
By substituting $-\theta$ for $\theta$ in above equations, we obtain
\begin{eqnarray*}\sin(180^{\circ}-\theta)&=&-\sin (-\theta)=\sin \theta\\ \cos(180^{\circ}-\theta)&=&-\cos (-\theta)=-\cos \theta\\\tan(180^{\circ}-\theta)&=&\tan (-\theta)=-\tan\theta\end{eqnarray*}
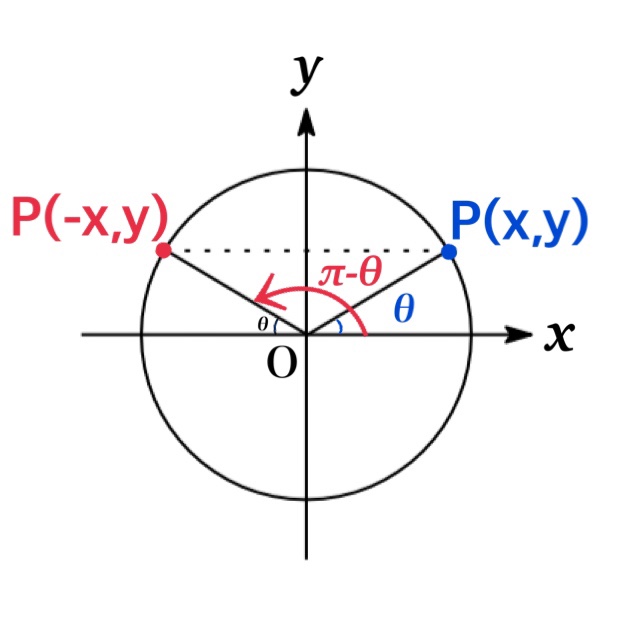
| Angel of ($\theta+2n\pi$) | |
| $\sin(360^{\circ}\times n +\theta)=\sin \theta$ | |
| $\cos(360^{\circ}\times n +\theta)=\cos \theta$ | |
| $\tan(360^{\circ}\times n +\theta)=\tan \theta$ |
Addition Formulas
| $\sin (x+ y)=\sin x\cos y+ \cos x\sin y$ | |
| $\cos (x + y)=\cos x\cos y- \sin x\sin y$ | |
| $\tan (x + y)=\frac{\tan x+\tan y}{1-\tan x\tan y}$ |
By substituting -y for y in above equations , we obtain the subtraction formulas \(\sin (x- y), \cos (x-y)\) and \(\tan (x-y)\).
Double-Angle Formulas
| By substituting x for y in above equations , we obtain the double-angle formulas \(\sin 2x, \cos 2x\) and \(\tan 2x\). → Check the details. | |
| $\sin 2x=2\sin x\cos y$ | |
| $\cos 2x=\cos^{2} x- \sin^{2} x=1-2\sin^{2}x=2\cos^{2} x-1$ | |
| $\tan 2x=\frac{2\tan x}{1-\tan^{2} x}$ |
Half-Angle Formulas
| By the double-angle formulas and the identity $\sin^{2} x+\cos^{2}x=1$, we obtain $\cos 2x=1-2\sin^{2}x=2\cos^{2} x -1$ and if we transform the equations, we get $\sin^{2} x=\frac{1-\cos 2x}{2}, \cos^{2} x=\frac{1+\cos 2x}{2}$. Then if we substitute $\frac{x}{2}$ for $x$, we get half-angel formulas. → Check the details. | |
| $\sin^{2}\frac{x}{2}=\frac{1-\cos x}{2}$ | |
| $\cos^{2}\frac{x}{2}=\frac{1+\cos x}{2}$ | |
| $\tan^{2}\frac{x}{2}=\frac{1-\cos x}{1+\cos x}$ |
Product and Sum Formulas
「Product to Sum」formulas can derived from addition formulas, and 「Sum to Product」formulas can be deduced 「Product to Sum」fomulas. → Check details.
| Sum → Product | |
| $\sin A+\sin B=2\sin \frac{A+B}{2}\cos\frac{A-B}{2}$ | |
| $\sin A-\sin B=2\sin \frac{A-B}{2}\cos\frac{A+B}{2}$ | |
| $\cos A+\cos B=2\cos \frac{A+B}{2}\cos\frac{A-B}{2}$ | |
| $\cos A-\cos B=-2\sin \frac{A+B}{2}\sin\frac{A-B}{2}$ |
| Product → Sum | |
| $2\sin A\cos B=\sin (A+B)+\sin (A-B)$ | |
| $2\cos A\sin B=\sin (A+B)-\sin (A-B)$ | |
| $2\cos A\cos B=\cos (A+B)+\cos (A-B)$ | |
| $2\sin A\sin B=-\{\cos (A+B)-\cos (A-B)\}$ |
Remark :There are many trigonometric identities, but notice that all can be deduced from the addition formula.
Transformation
Let $A$ and $B$ be constants. Then $A\sin \theta+B\cos \theta$ can be transformed as below:
$$A\sin \theta+B\cos \theta=\sqrt{A^{2}+B^{2}}\sin (\theta +\alpha)$$
where $\cos \alpha=\frac{A}{\sqrt{A^{2}+B^{2}}}, \ \sin \alpha=\frac{B}{\sqrt{A^{2}+B^{2}}}$
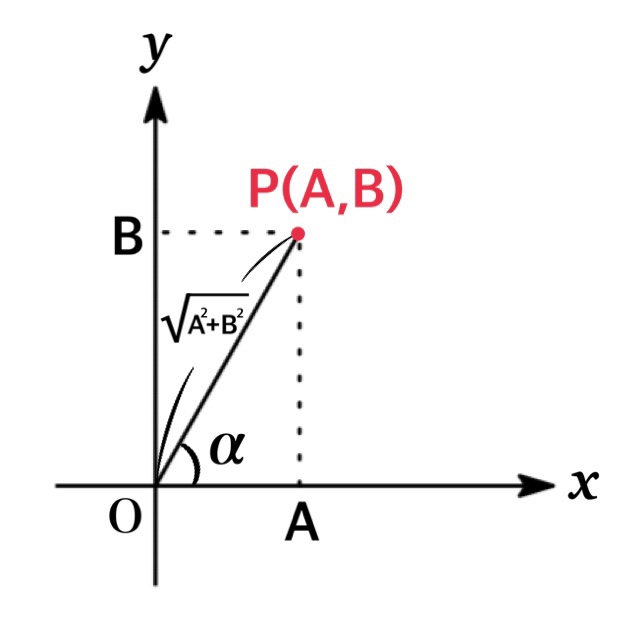
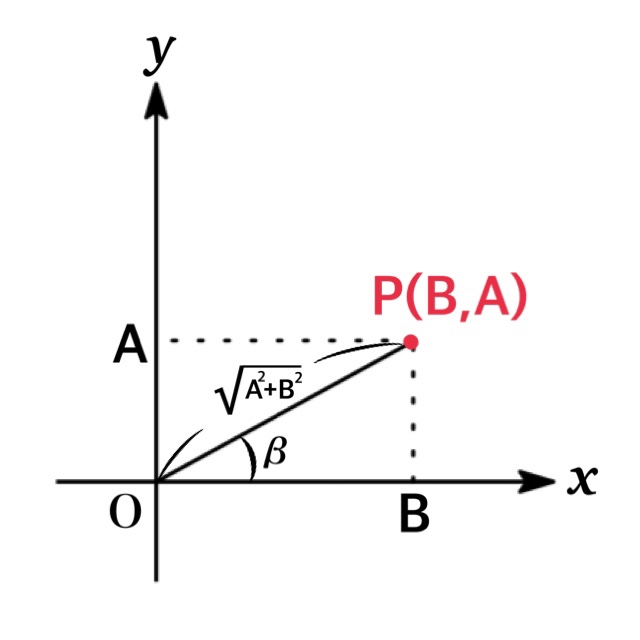
Remark:The form can be transformed as $\sqrt{A^{2}+B^{2}}\cos (\theta -\beta)$ :
$$A\sin \theta+B\cos \theta=\sqrt{A^{2}+B^{2}}\cos (\theta -\beta)$$
where $\sin \beta=\frac{A}{\sqrt{A^{2}+B^{2}}}, \ \cos \beta=\frac{B}{\sqrt{A^{2}+B^{2}}}$
Differentiation
| $(\sin x)’=\cos x$ | |
| $(\cos x)’=-\sin x$ | |
| $(\tan x)’=\frac{1}{\cos^{2} x}$ | |
| $(\mathrm{csc}\ x)’=-\mathrm{csc}\ x \cdot\mathrm{cot}\ x$ | |
| $(\mathrm{sec}\ x)’=\mathrm{sec}\ x \cdot\mathrm{tan}\ x$ | |
| $(\mathrm{cot}\ x)’=-\mathrm{csc}^{2}\ x$ |
Integrals
| $\int \sin x\ dx=-\cos x +C$ | |
| $\int \cos x\ dx=\sin x +C$ | |
| $\int \tan x\ dx=\ln |\sec x| +C$ | |
| $\int \csc x\ dx=\ln |\csc x-\cot x|+C$ | |
| $\int \sec x\ dx=\ln |\sec x+\tan x|+C$ | |
| $\int \cot x\ dx=\ln |\sin x|+C$ |