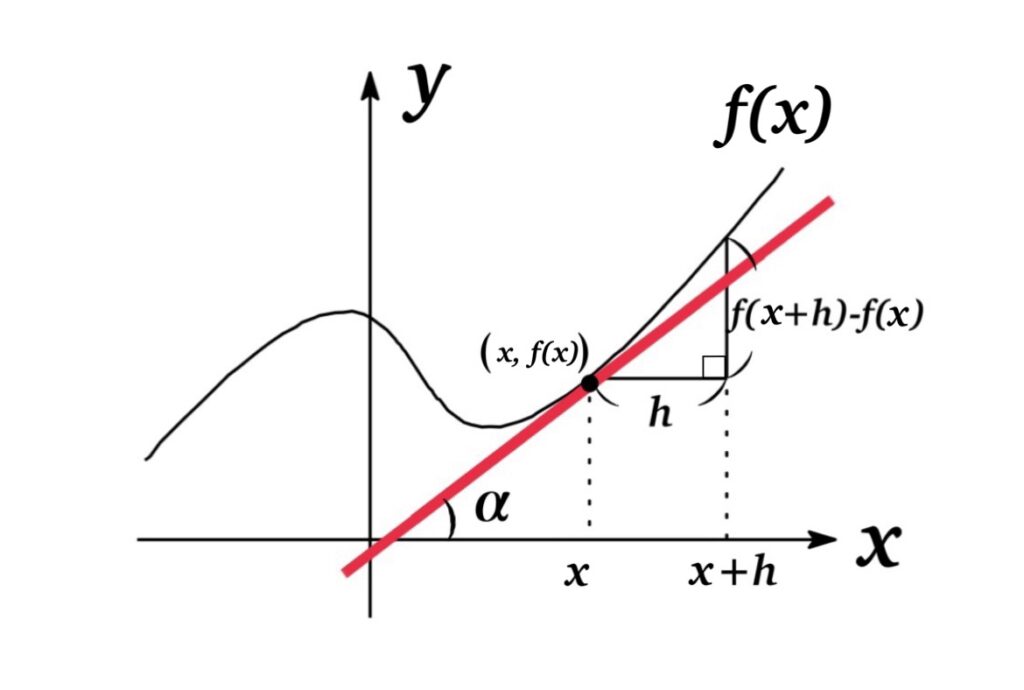
The definition of the derivative of $f$ is given by
$$\frac{d}{dx}f(x)=f'(x)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x+h)-f(x)}{h}$$
$f'(x)$ is the value of $f’$ at $x$ and this can be interpreted geometrically as the slope of the tangent line to the graph of $f$ at the point $(x,f(x))$.
Contents
Basic
| Expression | |
| Constant | \(\frac{d}{dx}[c]=0 \) |
| Power Functions | \(\frac{d}{dx}[x^{n}]=nx^{n-1} \) |
| Constant Multiple | \(\frac{d}{dx}[cf(x)]=cf'(x) \) |
| Sum/ Difference | \(\frac{d}{dx}[f(x)\pm g(x)]=f'(x)\pm g'(x) \) |
| Product | \(\frac{d}{dx}[f(x)g(x)]=f'(x)g(x)+g'(x)f(x) \) |
| Quotient | \(\frac{d}{dx}[\frac{f(x)}{g(x)}]=\frac{f'(x)g(x)-g'(x)f(x)}{g^{2}(x)} \) |
| Chain Rule | \(\frac{d}{dx}[f\left(g(x)\right)]=f’\left(g(x)\right)g'(x) \) |
| Inverse Functions | \(\frac{d}{dx}f^{-1}(x)=\frac{dy}{dx}=\frac{1}{\ \frac{dx}{dy}\ }=\frac{1}{f'(y)}\) where \(f(y)=x\) |
Derivative of Functions
Logarithmic and Exponential Functions
| Expression | |
| Exponential Function w/ Base \(\mathrm{e}\) | \(\frac{d}{dx}[\mathrm{e}^{x}]=\mathrm{e}^{x} \) |
| w/ Base \(a\) | \(\frac{d}{dx}[a^{x}]=a^{x}\log_{e} a \) |
| Natural Logarithmic | \(\frac{d}{dx}[\log_{e} x]=\frac{1}{x} \) |
| Logarithmic w/ Base \(a\) | \(\frac{d}{dx}[\log_{a} x]=\frac{1}{x\log_{e} a} \) |
Trigonometric Functions
| \(\frac{d}{dx} (\sin x)=\cos x\) | |
| \(\frac{d}{dx} (\cos x)=-\sin x\) | |
| \(\frac{d}{dx} (\tan x)=\frac{1}{\cos^{2} x}=\sec^{2} x\) | |
| \(\frac{d}{dx} (\mathrm{cosec} x)=\frac{d}{dx} (\frac{1}{\sin x})=-\frac{\cos x}{\sin^{2} x}=-\mathrm{cosec} x\cdot \cot x\) | |
| \(\frac{d}{dx} (\mathrm{sec} x)=\frac{d}{dx} (\frac{1}{\cos x})=\frac{\sin x}{\cos^{2} x}=\mathrm{sec} x\cdot \tan x\) | |
| \(\frac{d}{dx} (\mathrm{cot} x)=\frac{d}{dx} (\frac{1}{\tan x})=-\frac{1}{\sin^{2} x}=-\mathrm{cosec}^{2} x\) |
Inverse Trigonometric Functions
| \(\frac{d}{dx} (\sin^{-1} x)=\frac{1}{\sqrt{1-x^{2}}}\) | |
| \(\frac{d}{dx} (\cos^{-1} x)=-\frac{1}{\sqrt{1-x^{2}}}\) | |
| \(\frac{d}{dx} (\tan^{-1} x)=-\frac{1}{1+x^{2}}\) | |
| \(\frac{d}{dx} (\sin^{-1} f(x))=\frac{f'(x)}{\sqrt{1-{f(x)}^{2}}}\) | |
| \(\frac{d}{dx} (\cos^{-1} f(x))=-\frac{f'(x)}{\sqrt{1-f(x)^{2}}}\) | |
| \(\frac{d}{dx} (\tan^{-1} f(x))=-\frac{1}{1+f(x)^{2}}\) |
Hyperbolic Functions
| \(\frac{d}{dx} (\sinh x)=\cosh x\) | |
| \(\frac{d}{dx} (\cosh x)=\sinh x\) | |
| \(\frac{d}{dx} (\tanh x)=\frac{1}{\cosh^{2} x}\) | |
| \(\frac{d}{dx} (\mathrm{csch}\ x)=-\mathrm{csch}\ x \cdot\mathrm{coth}\ x\) | |
| \(\frac{d}{dx} (\mathrm{sech}\ x)=-\mathrm{sech}\ x \cdot\mathrm{tanh}\ x\) | |
| \(\frac{d}{dx} (\mathrm{coth}\ x)=-\mathrm{csch}^{2}\ x\) |
Inverse Hyperbolic Functions
| \(\frac{d}{dx} (\sinh^{-1}x)=\frac{1}{\sqrt{1+x^{2}}}\) | |
| \(\frac{d}{dx}(\cosh^{-1}x)=\frac{1}{\sqrt{x^{2}-1}}\) | |
| \(\frac{d}{dx}(\tanh^{-1}x)=\frac{1}{1-x^{2}}\) |
Logarithmic Differentiation
This is the meathod of differentiation by taking logarithms of both sides of an equation \(y=f(x)\). The calculation of derivatives of complicated functions involving products, quotients, or powers can often be simplified by taking logarithms.
\(y=f(x)\ \ \ \longrightarrow \ \ \ \log |y|=\log |f(x)|\ \ \ \longrightarrow \ \ \ \frac{y’}{y}=\frac{d}{dx}\log |f(x)|\)Derivatives of Inverse Functions
If \(f(x)\) is a one-to-one differential function with inverse functions \(f^{-1}(x)\), then its derivative is given
$$\frac{d}{dx}f^{-1}(x)=\frac{dy}{dx}=\frac{1}{\ \frac{dx}{dy}\ }=\frac{1}{f'(y)}$$
where \(f(y)=x\). See also ▶ Inverse Functions.
Parametric Equations
In the case of differentiation of parametric equations \(x=f(t)\) and \(y=g(t)\), we have
$$\frac{dy}{dx}=\frac{\ \ \ \frac{dy}{dt}\ \ \ }{\ \ \ \frac{dx}{dt}\ \ \ }=\frac{g'(t)}{f'(t)}\ \ \ \ \ \text{if}\ \ \ \frac{dx}{dt}\not= 0$$
Notice that the curve, defined by parametric equations \(x=f(t)\) and \(y=g(t)\), has a horizontal tangent when \(\frac{dy}{dt}=0\) and has a vertical tangent when \(\frac{dx}{dt}=0\).
Implicit Differentiation
Implicit functions are defined implicitly by a relation between \(x\) and \(y\) , whose function has the form \(f(x,y)=0\). (On the other side, the explicit functions are expressed by one variable x, such as \(y=f(x)\).)
Example of an implicit function : \(x^{2}+y^{2}=5\)
In the case of the differentiation of implicit functions, we differentiate both sides of the equation with respect to x by using the Chain Rule, and solve the resulting equation for \(y’\).
Example: \(\frac{d}{dx}(x^{2}+y^{2})=\frac{d}{dx}(25)\ \ \ \longrightarrow \ \ \ 2x+2y \frac{dy}{dx}=0\ \ \ \longrightarrow \ \ \ y’=\frac{dy}{dx}=-\frac{x}{y}\)
Higher Derivatives
The \(n\)th derivative of \(f\) is a function obtained from \(f\) by differentiating \(n\) times, and denoted by \(f^{(n)}\). If \(y=f(x)\), we have alternative notations for the \(n\)th derivatives as below:
$$y^{(n)}=f^{(n)}(x)=\frac{d^{n}}{dx^{n}}f(x)=D^{n}f(x)$$
General Leibniz rule
Suppose that \(f(x)\) and \(g(x)\) are n-times differentiable functions. Then \(n\)-th derivative of \(f(x)g(x)\) is given by
$$\{f(x)g(x)\}^{(n)}=\frac{d^{n}}{dx^{n}}f(x)g(x)=\sum_{i=0}^{n} { }_{n}C_{i} f^{(i)}(x)g^{(n-i)}(x)$$
where \({}_{n} C_{i}=\frac{n!}{i!(n-i)!}\) is the binomial coefficient and \(f^{(i)}(x)\) denotes the \(i\)th derivative of \(f\). Notice that in particular \(f^{(0)}(x)=f(x)\).
See also ▶ details and examples.