A quadratic function is a polynomial of degree 2 which has the form
$$f(x)=ax^{2}+bx+c$$
where \(x\) is an unknown and where \(a, b\) and \(c\) are constants with \(a\not=0\).
Quadratic Formula
The quadratic formula provides the solutions to a quadratic equation. \(ax^{2}+bx+c=0\) where \(a\not= 0\). That is, the quadratic equation has two solutions:
$$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$$
This formula indicates that can be factored into as below:
$$ax^{2}+bx+c=a(x-\frac{-b+\sqrt{b^{2}-4ac}}{2a})(x-\frac{-b-\sqrt{b^{2}-4ac}}{2a})=0$$
The geometric interpretation is that \(y=ax^{2}+bx+c\) intersects with \(x\)-axis at \((\frac{-b-\sqrt{b^{2}-4ac}}{2a}, 0)\) and \((\frac{-b+\sqrt{b^{2}-4ac}}{2a}, 0)\) if \(b^{2}-4ac\geq 0\).
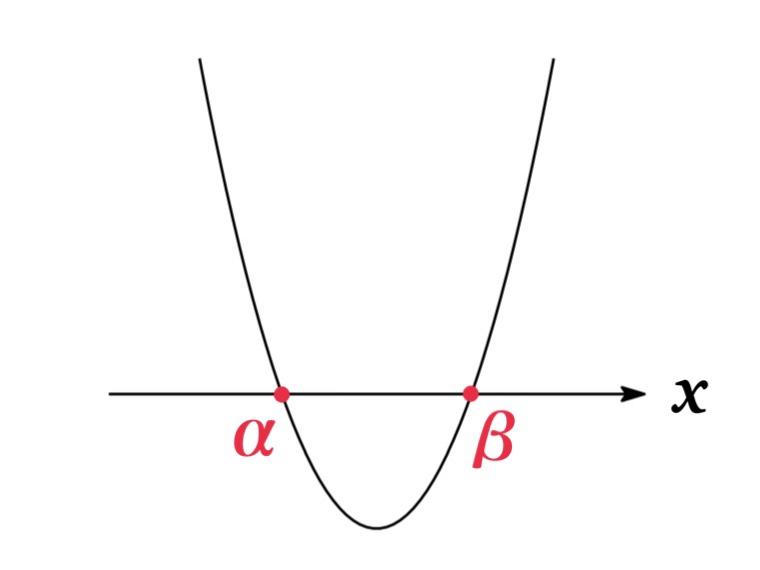
The number of solutions
| Discriminant | Intersections of \(y=ax^{2}+bx+c\) and \(x\) axis | Solutions of \(ax^{2}+bx+c=0\) | |
| Example 1 | \(b^{2}-4ac>0\) | two intersections | Distinct two solutions: \(x=\frac{-b-\sqrt{b^{2}-4ac}}{2a}, \frac{-b+\sqrt{b^{2}-4ac}}{2a}\) |
| Example 2 | \(b^{2}-4ac=0\) | one intersection | Repeated root: \(x=\frac{-b}{2a}\) |
| Example 3 | \(b^{2}-4ac<0\) | no intersection | None in real numbers: \(x=\frac{-b-\sqrt{(4ac-b^{2})}\ i}{2a}, \frac{-b+\sqrt{(4ac-b^{2})}\ i}{2a}\) |

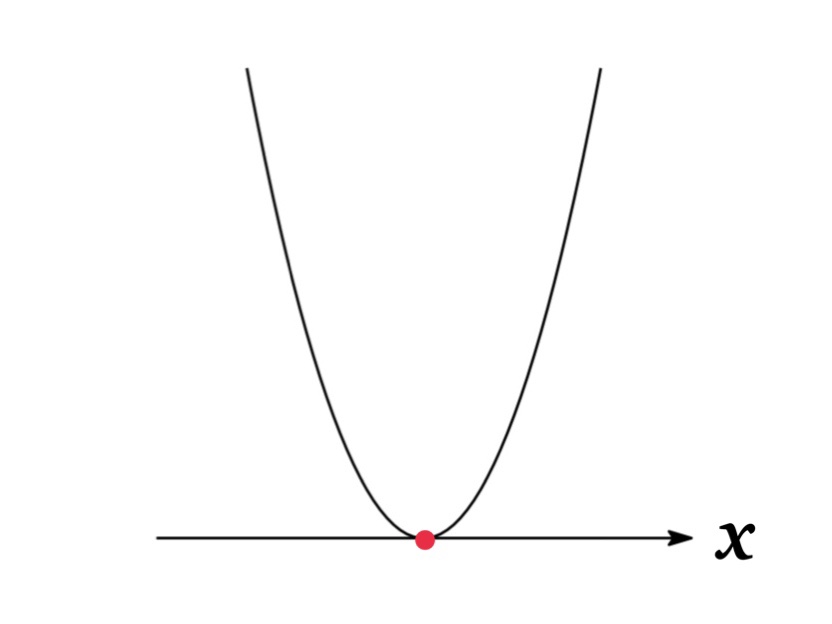
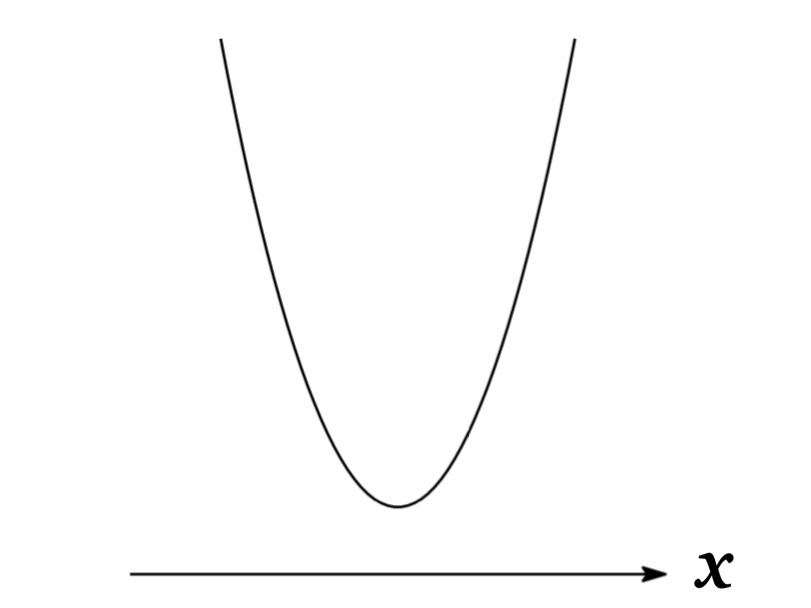
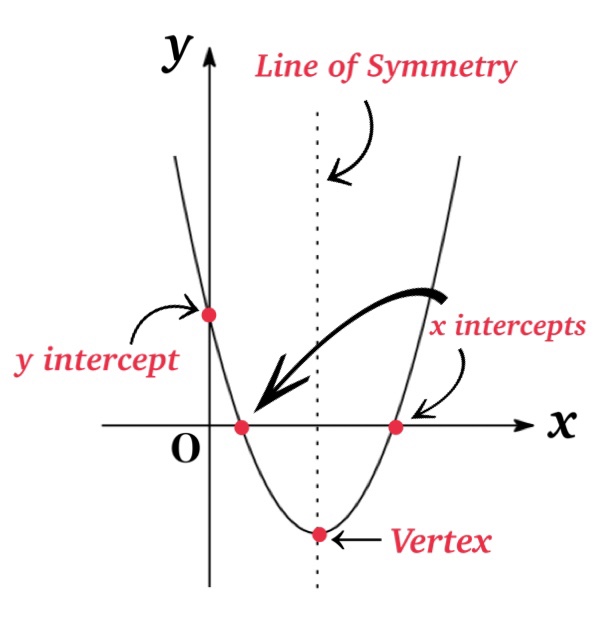
Graphs
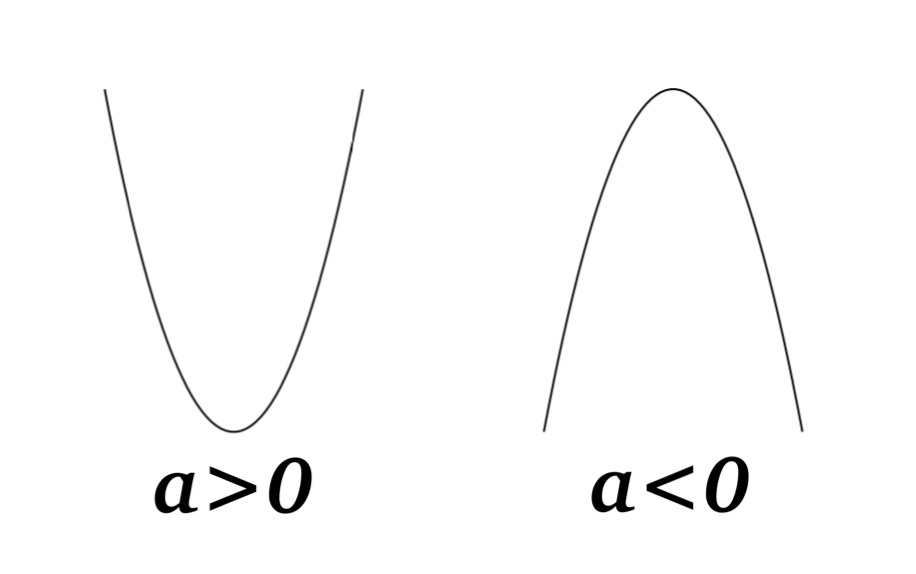
The shape of \(y=ax^{2}+bx+c\) is called parabola and the leading coefficient, \(a\) , determine the parabola opens upward or downward.
As shown in Fig, if \(a\) is positive, the parabola opens upward, and if \(a\) is negative, the parabola opens downward.
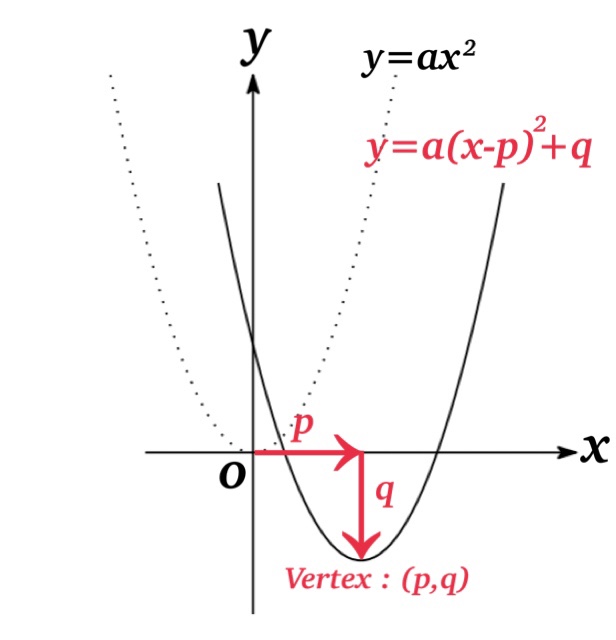
$$ax^{2}+bx+c=a\left(x+\frac{b}{2a}\right)^{2}-\frac{b^{2}-4ac}{4a}$$
and this will tell us the vertex and the vertical line of symmetry.
| \(x\)-intercepts | \((\frac{-b-\sqrt{b^{2}-4ac}}{2a}, 0)\) and \((\frac{-b+\sqrt{b^{2}-4ac}}{2a},0)\) |
| \(y\)-intercept | \((0, c)\) |
| Vertex | \((\frac{b}{2a}, -\frac{b^{2}-4ac}{4a})\) |
| Line of Symmetry | \(x=-\frac{b}{2a}\) |
Notice that not all quadratic function have intercepts, but only quadratic functions whose discriminants is \(D\geq 0\) have two intercepts or one intercept.
Furthermore, the graph of \(y=ax^{2}+bx+c\) is given by shifting the graph \(y=ax^{2}\) horizontally \(-\frac{b}{2a}\) and vertically \(-\frac{b^{2}-4ac}{4a}\).
Inequality
Let \(\alpha\) and \(\beta\) be the solutions to \(ax^{2}+bx+c=0\). Then \(\alpha\) and \(\beta\) are the intersections of \(y=ax^{2}+bx+c\) and \(x\) axis, the solutions to inequality are given as below:
| \(a>0\) | Solutions |
| \(ax^{2}+bx+c>0\) | \(x<\alpha,\ \beta<x\) |
| \(ax^{2}+bx+c<0\). | \(\alpha<x<\beta\) |
| \(a<0\) | Solutions |
| \(ax^{2}+bx+c>0\) | \(\alpha<x<\beta\) |
| \(ax^{2}+bx+c<0\). | \(x<\alpha,\ \beta<x\) |