$$\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{x}=1 \ \ \ ( x \text{ is radian measure} )$$
Proof :
We use a geometric argument to prove the limit value.
We first prove that the right limit value \(\displaystyle\lim_{x\rightarrow +0}\frac{\sin x}{x}\) is equal to 1.
Suppose that x lies between \(0\) and \(\frac{\pi}{2}\).
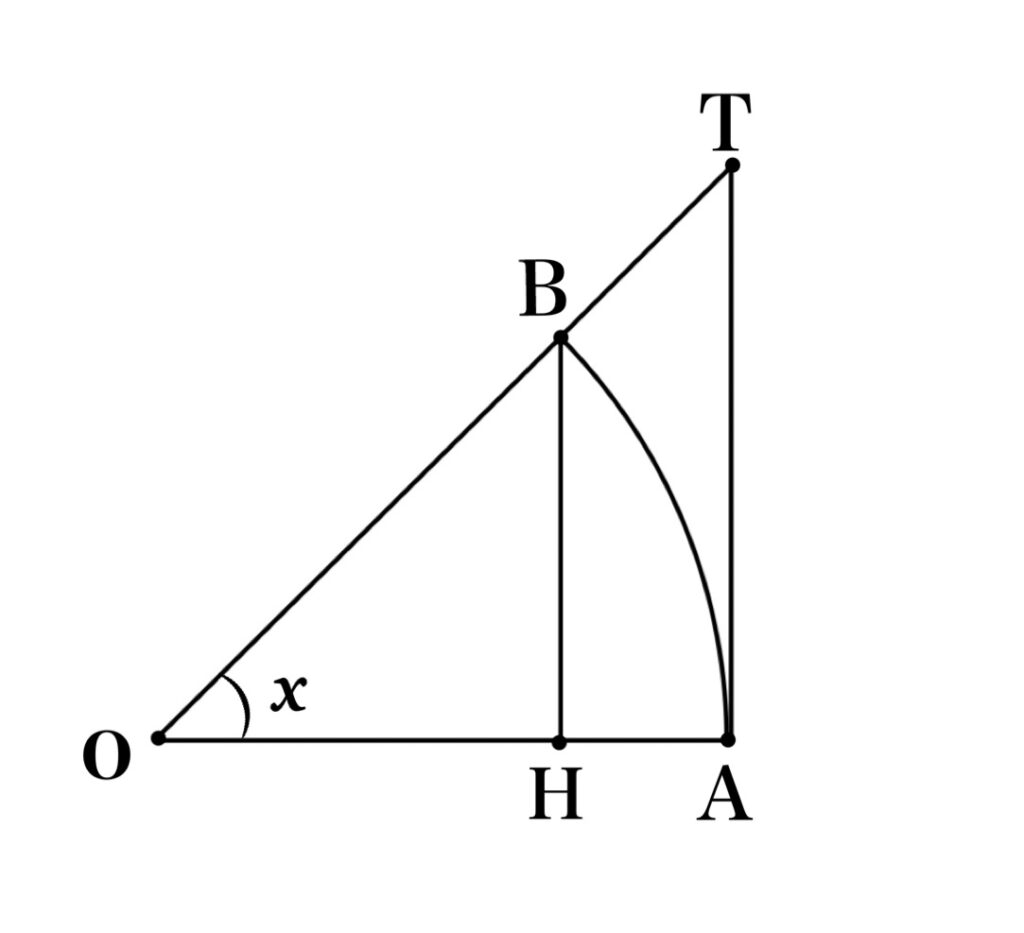
Consider a sector OAB with radius of 1 and central angle of x as shown in the figure on the right. Let BH be the perpendicular line drawn to the line segment OA from B, and AT be the perpendicular line drawn to A from the straight line OB.
Since \(|BH|=\sin x\), the area of \(\triangle OAB=\frac{\sin x}{2}\), and the area of the sector is \(\frac {x}{2}\). Also, since \(|AT|=\tan x\), the area of \(\triangle OAT=\frac{\tan x}{2}\). From the diagram, we see that
$$\triangle OAB < \text{ sector } OAB < \triangle OAT$$
Therefore we have
$$\frac{\sin x}{2}<\frac{x}{2}<\frac{\tan x}{2}$$
If we multiply each sides of the inequality by \(\frac{2}{\sin x}\), we obtain
$$1<\frac{x}{\sin x} <\frac{1}{\cos x}$$
and if we take the reciprocal on each sides, we obtain
$$1>\frac{\sin x}{x}>\cos x$$
Now we know that \(\displaystyle\lim_{x\rightarrow +0} \cos x=1\), so by the Squeeze Theorem, we get
$$\displaystyle\lim_{x\rightarrow +0}\frac{\sin x}{x}=1$$
To prove the left limit \(\displaystyle\lim_{x\rightarrow -0}\frac{\sin x}{x} =1\) , we set \(t=-x\) on \(\displaystyle\lim_{x\rightarrow +0}\frac{\sin x}{x}=1\). Then we have \(t\rightarrow +0\) when \(x\rightarrow -0\). Thus we obtain
$$\displaystyle\lim_{x\rightarrow -0}\frac{\sin x}{x}=\displaystyle\lim_{x\rightarrow -0}\frac{-\sin x}{-x}=\displaystyle\lim_{x\rightarrow -0}\frac{\sin (-x)}{(-x)}=\displaystyle\lim_{t\rightarrow +0}\frac{\sin t}{t}=1$$
Therefore we have proved \(\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{x}=1\).
(Or we can prove the left limit \(\displaystyle\lim_{x\rightarrow -0}\frac{\sin x}{x} =1\) by using the property of an even function. That is the function \(\frac{\sin x}{x}\) is an even function. Thus its right and left limits must be equal.)