$$\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{x}=1 \ \ \ ( x \text{は弧度法} )$$
証明
証明 :
まず右側極限値 $\displaystyle\lim_{x\rightarrow +0}\frac{\sin x}{x}$ が 1 であることを示す.
$x$ は $0 < x <\frac{\pi}{2}$ の範囲にあるとする.
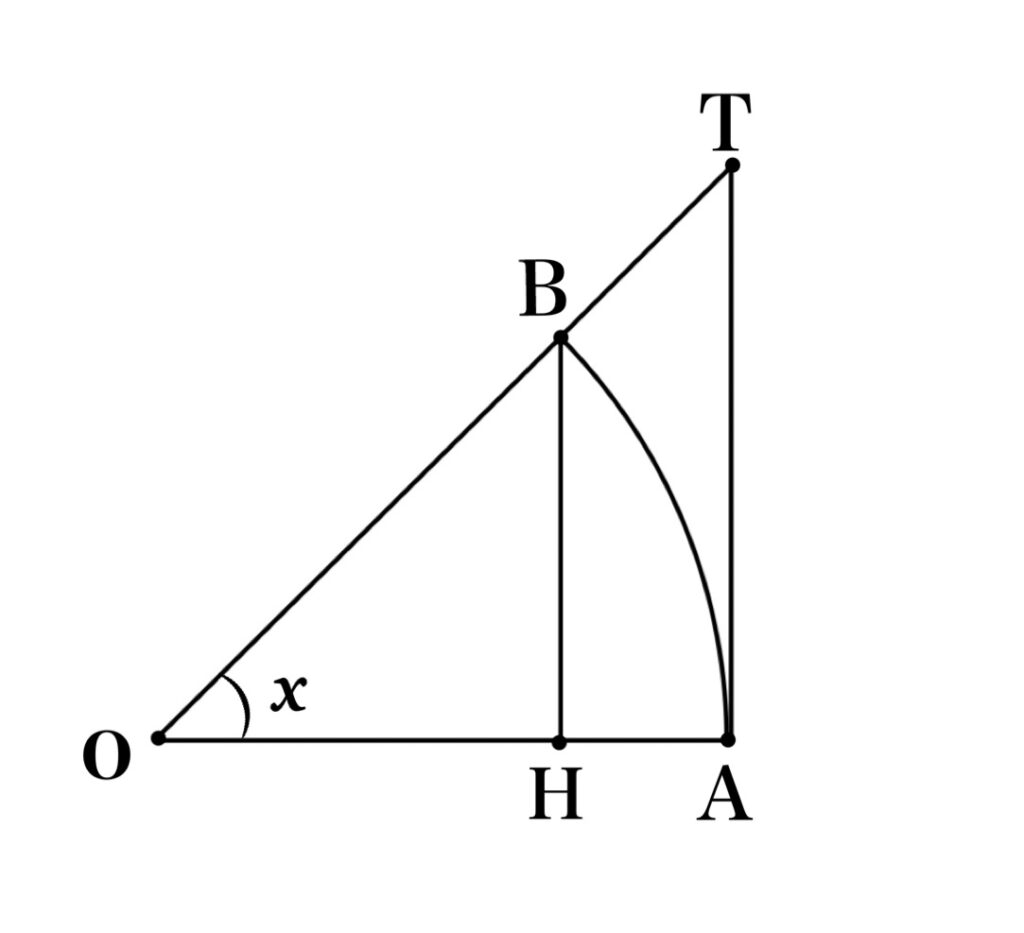
左図のように半径 1, 中心角 x の扇形 OAB を考える. B より線分 OA にひいた垂線を BH, A より直線 OB にひいた垂線を AT とする.
$BH=\sin x$ より $\triangle OAB=\frac{\sin x}{2}$, 扇形の面積は $\frac{x}{2}$ である. また $AT=\tan x$ より $\triangle OAT=\frac{\tan x}{2}$ となる. このとき
$$\triangle OAB < \text{扇形 } OAB < \triangle OAT$$
よって
$$\frac{\sin x}{2}<\frac{x}{2}<\frac{\tan x}{2}$$
となる. 各辺に $\frac{2}{\sin x}$ をかけると
$$1<\frac{x}{\sin x} <\frac{1}{\cos x}$$
ここで逆数をとると
$$1>\frac{\sin x}{x}>\cos x$$
となる. このとき $\displaystyle\lim_{x\rightarrow +0} \cos x=1$ なので, はさみうちの原理より
$$\displaystyle\lim_{x\rightarrow +0}\frac{\sin x}{x}=1$$
となる. 左側極限値 $\displaystyle\lim_{x\rightarrow -0}\frac{\sin x}{x} =1$ であることを示すためには, $\displaystyle\lim_{x\rightarrow +0}\frac{\sin x}{x}=1$ において $t=-x$ とおけば, $x\rightarrow -0$ のとき $t\rightarrow +0$ より
$$\displaystyle\lim_{x\rightarrow -0}\frac{\sin x}{x}=\displaystyle\lim_{x\rightarrow -0}\frac{-\sin x}{-x}=\displaystyle\lim_{x\rightarrow -0}\frac{\sin (-x)}{(-x)}=\displaystyle\lim_{t\rightarrow +0}\frac{\sin t}{t}=1$$
を得る.
よって $\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{x}=1$ が示された.
(左側極限値 $\displaystyle\lim_{x\rightarrow -0}\frac{\sin x}{x} =1$ であることは偶関数の性質を用いて証明することもできる. すなわち 関数 $\frac{\sin x}{x}$ は偶関数であるので, 右側極限値と左側極限値が等しくなることを利用すれば良い. )