z を複素数 $z=r(\cos \theta+i\sin \theta)$, n を自然数とするとき, 方程式 $\omega^{n}=z$ の解は
$$\omega_{k}=r^{\frac{1}{n}}\{\cos \left(\frac{\theta+2k\pi}{n}\right)+i\sin \left(\frac{\theta+2k\pi}{n}\right)\}\ (k=0,1,\cdots, n-1)$$
で与えられる.
$ \omega^{n}=z$ の解 $\omega$ を, 複素数 $z$ の n 乗根という.
複素数の n 乗根は、複素数解の範囲で n 個存在する. また $\omega_{k}$ は点 $\omega_{0}$ を1つの頂点として, $n\geq 3$ ならば 半径 $\sqrt[n]{r}$ の円に内接する正 $n$ 角形の頂点となる.
Remark :$\omega_{k}=\omega_{0}z_{k}$ ( $z_{k}$ は $1$ の $n$ 乗根) で表される.
例
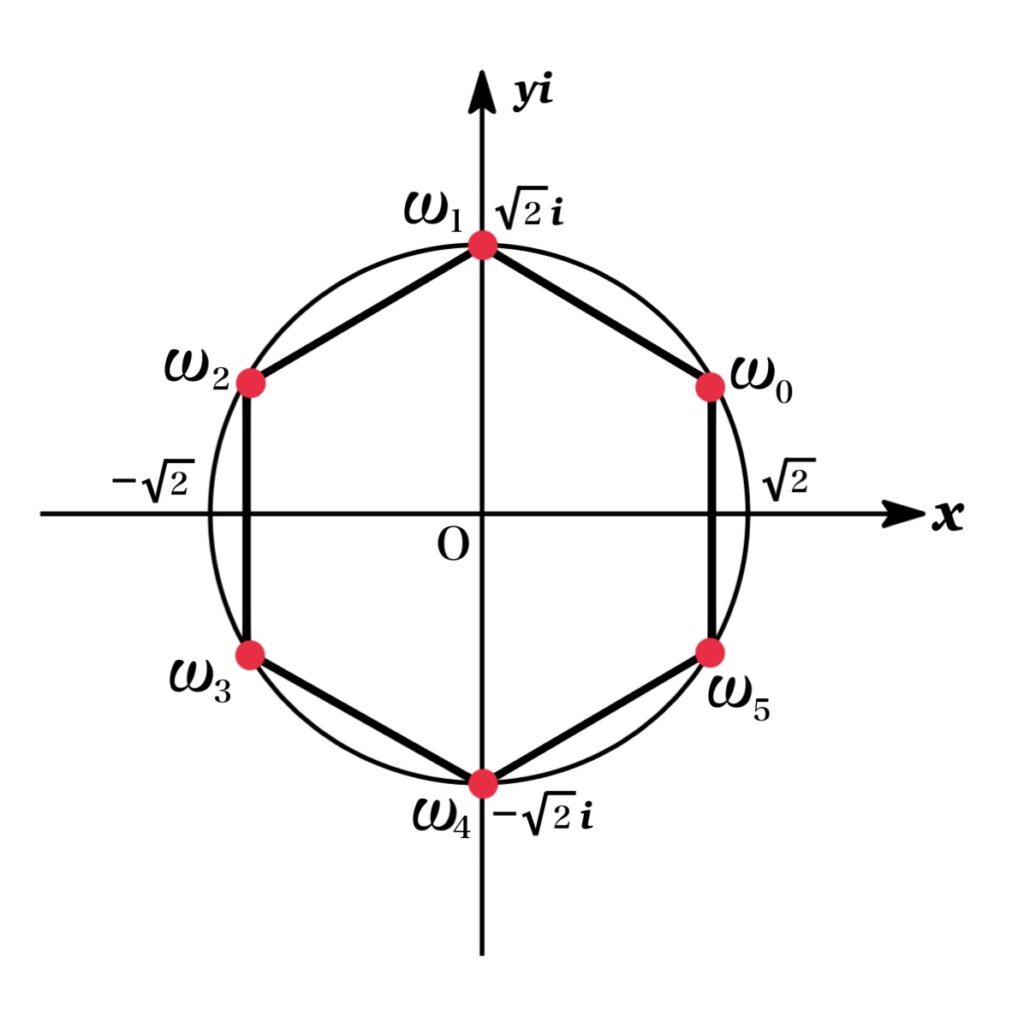
方程式 $\omega^{6}=8$ を解け.
$z=8$ の6乗根, すなわち, $\omega^{6}=8$ の解を求める.
このとき $z=8=8(\cos \pi+i\sin\pi)$ である. したがって $\omega^{6}=8$ の解は
$$\omega_{k}=\sqrt[6]{8}\{\cos \left(\frac{\pi+2k\pi}{6}+i\sin \frac{\pi+2k\pi}{6}\right)\}\ (k=0,1,2,3,4,5)$$
で表されるので、求める解は
$$\begin{eqnarray*}\omega_{0}&=&8^{\frac{1}{6}}(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6})=\sqrt{2}\left(\frac{\sqrt{3}+i}{2}\right)\\\omega_{1}&=&8^{\frac{1}{6}}(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2})=\sqrt{2}i\\\omega_{2}&=&8^{\frac{1}{6}}(\cos \frac{5\pi}{6}+i\sin \frac{5\pi}{6})=\sqrt{2}\left(\frac{-\sqrt{3}+i}{2}\right)\\\omega_{3}&=&8^{\frac{1}{6}}(\cos \frac{7\pi}{6}+i\sin \frac{7\pi}{6})=\sqrt{2}\left(\frac{-\sqrt{3}-i}{2}\right)\\\omega_{4}&=&8^{\frac{1}{6}}(\cos \frac{3\pi}{2}+i\sin \frac{3\pi}{2})=-\sqrt{2}i\\\omega_{5}&=&8^{\frac{1}{6}}(\cos \frac{11\pi}{6}+i\sin \frac{11\pi}{6})=\sqrt{2}\left(\frac{\sqrt{3}-i}{2}\right)\\\end{eqnarray*}$$
となる.
証明
$\omega^{n}=z$ の解を求める.
$$\begin{eqnarray*}z&=&r(\cos \theta+i\sin \theta)\\\omega&=&s(\cos \lambda+i\sin \lambda)\end{eqnarray*}$$とおく. ド・モアブルの定理より
$$\omega^{n}=s^{n}(\cos n\lambda+i\sin n\lambda)=r(\cos \theta+i\sin \theta)\ \cdots (\text{*})$$
このとき(*)を満たす$s, \lambda$の値を求める. 両辺の絶対値と偏角を比較すると
$$\begin{eqnarray*}s^{n}&=&r\\ n\lambda&=&\theta+(2\pi\times k)\ (k\text{は整数})\end{eqnarray*}$$
より, これらを満たす$s, \lambda$ は
$$\begin{eqnarray*}s&=&r^{\frac{1}{n}}\\\lambda&=&\frac{\theta+2k\pi}{n}\ (k=0,1,\cdots, n-1)\end{eqnarray*}$$
となるので, $\omega^{n}=z$ の解は次のように与えられる.
$$\omega_{k}=r^{\frac{1}{n}}\{\cos \left(\frac{\theta+2k\pi}{n}\right)+i\sin \left(\frac{\theta+2k\pi}{n}\right)\}\ (k=0,1,\cdots, n-1)$$
関連記事
- 1の n 乗根
- ド・モアブルの法則