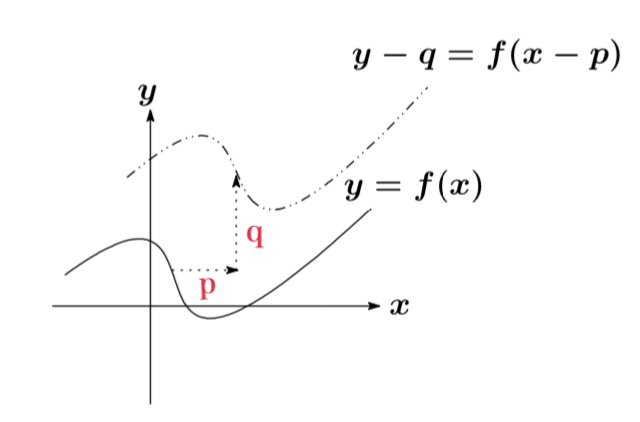
$y=f(x)$ を 「x 軸方向に p」, 「y 軸方向に q 」だけ平行移動した方程式は
$$y-q=f(x-p)$$で表される.
$y=f(x)$ 上の任意の点 $(x,y)$ を 「x 軸方向に p」 , 「 y 軸方向に q 」だけ平行移動させた点を $(X,Y)$とする.
このとき $X=x+p,\ Y=y+q$ で表されるので
$$x=X-p,\ y=Y-q$$
となる. このとき、平行移動させた点 $(X,Y)$ が満たす関係式を求めればよいので
$$Y-q=f(X-p)$$
が求めたい方程式である.
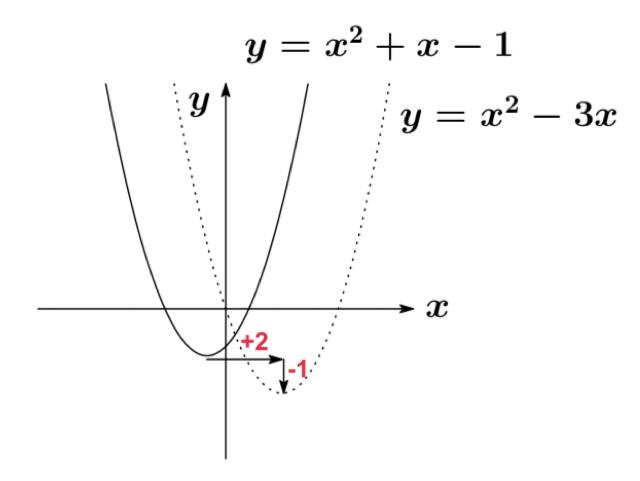
例
$y=x^{2}+x-1$ のグラフを 「x 軸方向に+2」, 「y 軸方向に -1」だけ平行移動したグラフの関数を求めよ.
グラフの平行移動の公式において,
$$f(x)=x^{2}+x-1,\ p=+2,\ q=-1$$
となるので, 平行移動させたグラフの関数は
$$y-(-1)=f(x-2)$$
となる. $f(x-2)=(x-2)^{2}+(x-2)-1$ となることに注意すれば, 求めたい方程式は次のように表される.
$$y=x^{2}-3x$$
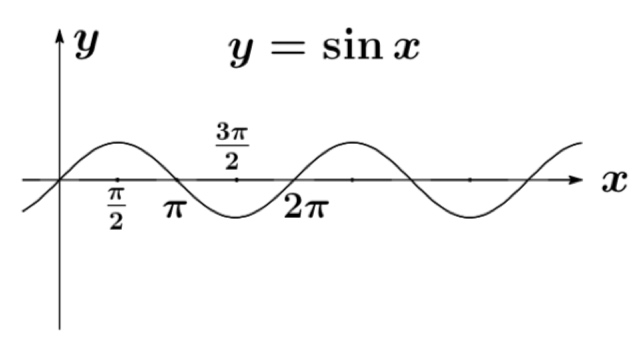
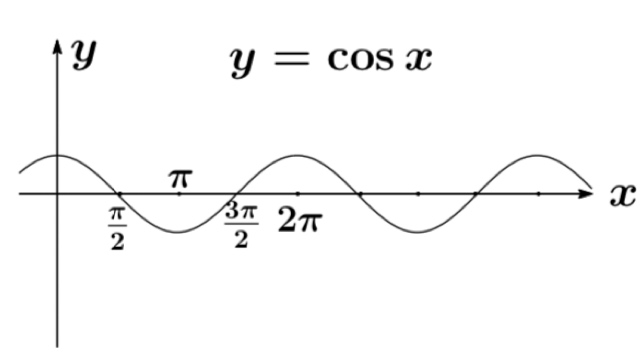
$\sin (x+\frac{\pi}{2})=\cos x,\ \ \cos (x+\frac{\pi}{2})=-\sin x,\ \ \tan (x+\frac{\pi}{2})=-\frac{1}{\tan x}$ について、グラフの平行移動の観点より考察せよ.
$\sin (x+\frac{\pi}{2})=\cos x $ について
$\sin x$ のグラフを x 軸方向に $-\frac{\pi}{2}$ 平行移動させたら, $\cos x$となる.
$\cos (x+\frac{\pi}{2})=-\sin x$ について
$\cos x$ のグラフを x 軸方向に $-\frac{\pi}{2}$ 平行移動させたら, $-\sin x$となる
$\tan (x+\frac{\pi}{2})=-\frac{1}{\tan x}$ について
$\tan (x+\frac{\pi}{2})=\frac{\sin (x+\frac{\pi}{2})}{\cos(x+\frac{\pi}{2})}=\frac{\cos x}{-\sin x}=-\frac{1}{\tan x}$