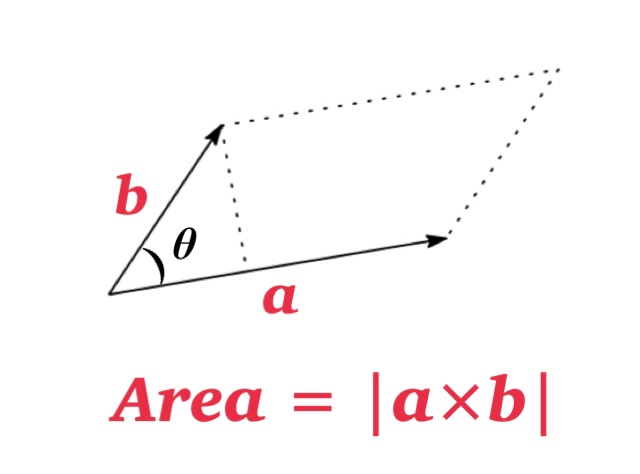
Let \(\theta\) be the angel between \(\mathbf{a}\) and \(\mathbf{b}\). Then
$$|\mathbf{a}\times \mathbf{b}|=|\mathbf{a}| |\mathbf{b}|\sin\theta$$
Notice that two nonzero vectors \(\mathbf{a}\) and \(\mathbf{b}\) are parallel if and only if \(\theta=0\) or \(\pi\). In either case \(\sin\theta=0\), so \(|\mathbf{a} \times \mathbf{b}|=0\) and therefore \(\mathbf{a} \times \mathbf{b}=0\).
Thus, two nonzero vectors \(\mathbf{a}\) and \(\mathbf{b}\) are parallel if and only if \(\mathbf{a} \times \mathbf{b}=0\).
Furthermore, this theorem give us the geometric description . See also Geometric Interpretation of Cross Products.
Contents
Proof
From the definition of the cross product and length of a vector, we have
$$\begin{eqnarray*}|\mathbf{a}\times \mathbf{b}|^{2}&=&(a_{2}b_{3}-a_{3}b_{2})^{2}+(a_{3}b_{1}-a_{1}b_{3})^{2}+(a_{1}b_{2}-a_{2}b_{1})^{2}\\&=&(a_{1}^{2}+a_{2}^{2}+a_{3}^{2})(b_{1}^{2}+b_{2}^{2}+b_{3}^{2})-(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3})^{2}\\&=&|\mathbf{a}|^{2} |\mathbf{b}|^{2}-(\mathbf{a}\cdot \mathbf{b})^{2}\\&=&|\mathbf{a}|^{2} |\mathbf{b}|^{2}-|\mathbf{a}|^{2} |\mathbf{b}|^{2}\cos^{2}\theta\\&=&|\mathbf{a}|^{2} |\mathbf{b}|^{2}(1-\cos^{2}\theta)\\&=&|\mathbf{a}|^{2} |\mathbf{b}|^{2}\sin^{2}\theta\end{eqnarray*}$$
Since \(0\leq \theta\leq \pi\), we have \(\sin \theta\geq 0\). Thus, \(\sqrt{\sin^{2}\theta}=\sin\theta\) and \(|\mathbf{a}\times \mathbf{b}|=|\mathbf{a}| |\mathbf{b}|\sin\theta\).
Rerated Articles
See also