We define the inverse hyperbolic functions as below : $$\begin{eqnarray*}y=\sinh^{-1}x &\Longleftrightarrow& \sinh y=x \\y=\cosh^{-1}x &\Longleftrightarrow& \cosh y=x \ \ (y\geq 0)\\y=\tanh^{-1}x &\Longleftrightarrow& \tanh y=x\end{eqnarray*}$$
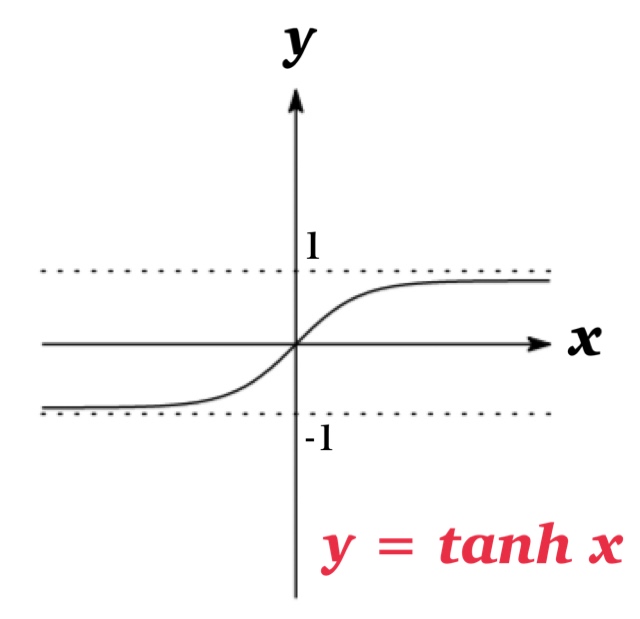
We can see that \(\sinh x\) and \(\tanh x\) are one-to-one, so they have inverse functions denoted by \(\sinh^{-1}x\) and \(\tanh^{-1}x\).
However, \(\cosh x\) is not one-to-one. Therefore we restrict the domain of \(\cosh x\) on \(0\leq x<\infty\).
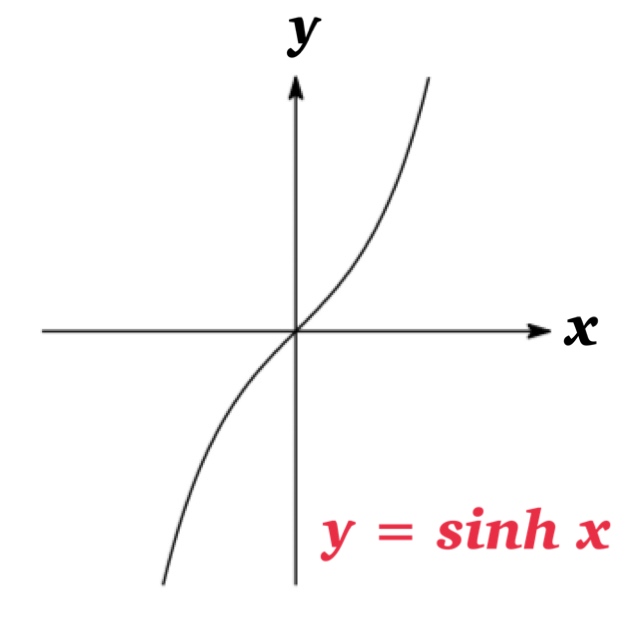
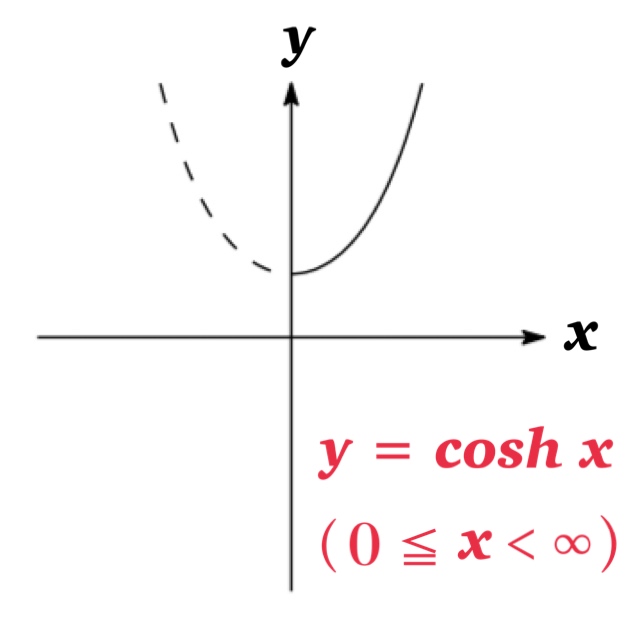
Then, it becomes one-to-one and we can define the inverse hyperbolic cosine function \(\cosh^{-1}x\).
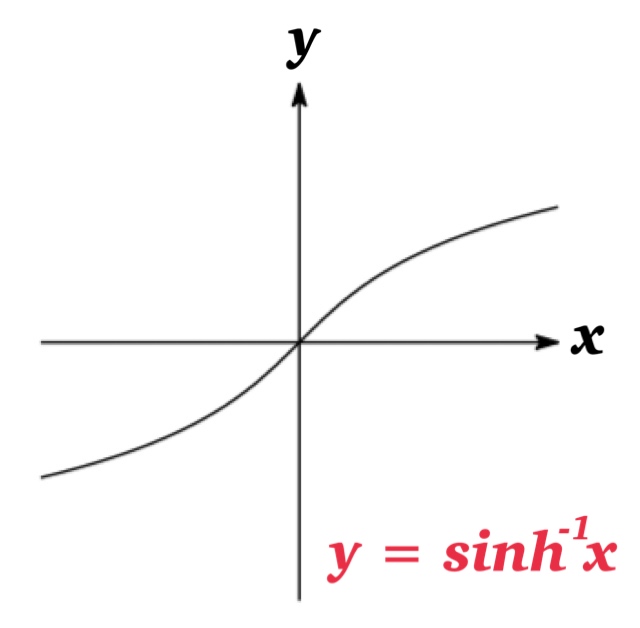
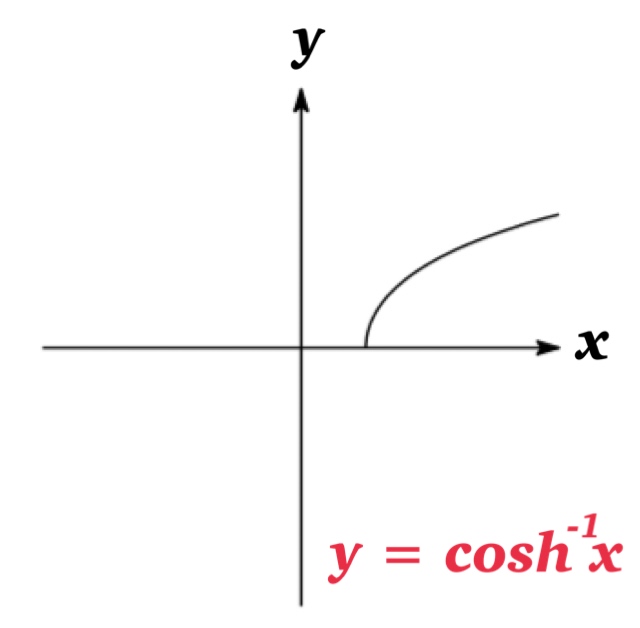
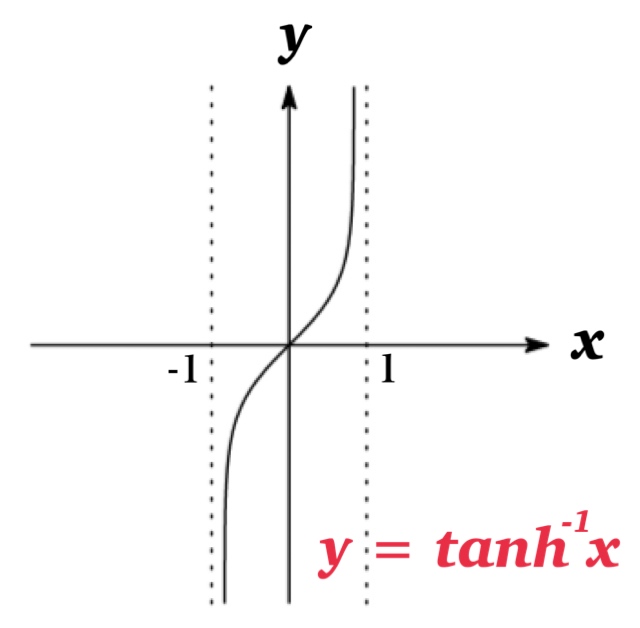
Expression by Logarithms
| \(\sinh^{-1}x=\log (x+\sqrt{x^{2}+1})\) |
| \(\cosh^{-1}x=\log (x+\sqrt{x^{2}-1})\) |
| \(\tanh^{-1}x=\frac{1}{2}\log\frac{1+x}{1-x}\) |
See also Inverse Hyperbolic Functions Expressed by Logarithms.
Derivatives
| \(\frac{d}{dx} (\sinh^{-1}x)=\frac{1}{\sqrt{1+x^{2}}}\) |
| \(\frac{d}{dx}(\cosh^{-1}x)=\frac{1}{\sqrt{x^{2}-1}}\) |
| \(\frac{d}{dx}(\tanh^{-1}x)=\frac{1}{1-x^{2}}\) |
| \(\frac{d}{dx} (\mathrm{csch}^{-1}\ x)=-\frac{1}{|x|\sqrt{1+x^{2}}}\) |
| \(\frac{d}{dx} (\mathrm{sech}^{-1}\ x)=-\frac{1}{x\sqrt{1-x^{2}}}\) |
| \(\frac{d}{dx} (\mathrm{coth}^{-1}\ x)=\frac{1}{1-x^{2}}\) |
Related Articles
- Inverse Functions
- One-to-One Functions
- Hyperbolic Functions