Implicit functions are defined implicitly by a relation between \(x\) and \(y\) , whose function has the form $$f(x,y)=0$$
On the other side, the explicit functions are expressed by one variable x, such as \(y=f(x)\).
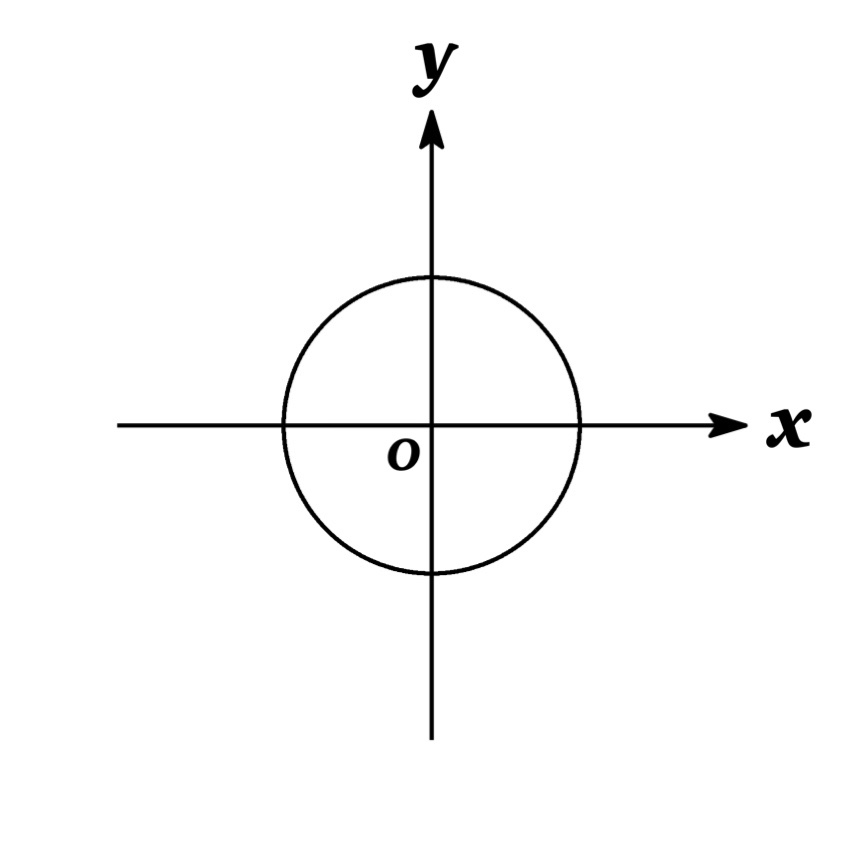
Example : \(x^{2}+y^{2}=5\)
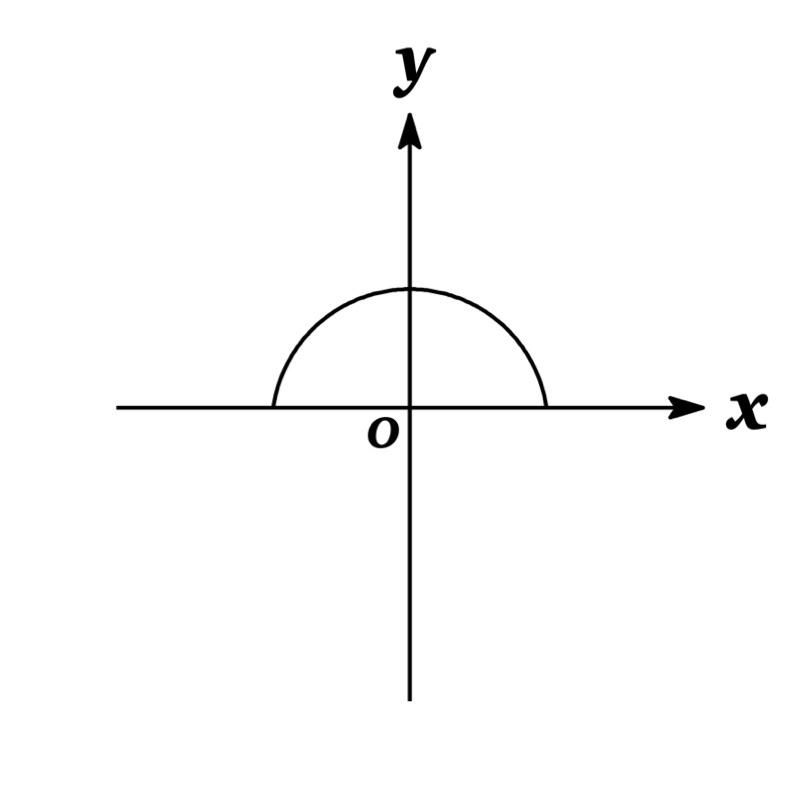
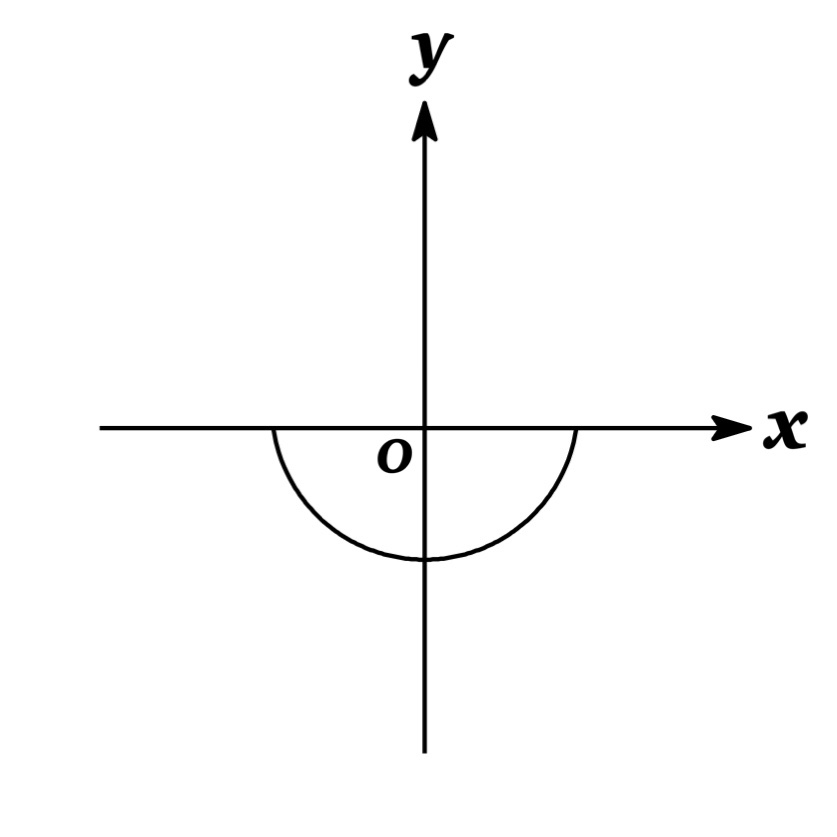
To express the implicit function as an explicit function of $x$, we need to solve the equation for $y$. Then, we get $y=\pm \sqrt{25-x^{2}}$. The graph of two functions $y=\sqrt{25-x^{2}}$ and $y=-\sqrt{25-x^{2}}$ are the upper and lower semicircles of the circle $x^{2}+y^{2}=25$ as shown in Figures below.
Differentiation
In the case of the differentiation of implicit functions, we differentiate both sides of the equation with respect to x by using the Chain Rule, and solve the resulting equation for \(y’\).
Example: Find $\frac{dy}{dx}$ if $x^{2}+y^{2}=25$.
Solution : Differentiate both side of the equation:
$$\frac{d}{dx}(x^{2}+y^{2})=\frac{d}{dx}(25)$$
Since $y$ is a function of $x$, applying the Chain Rule, we get
$$\frac{d}{dx}\left( y^{2} \right)=\frac{d}{dy}\left(y^{2}\right)\frac{dy}{dx} =2y\frac{dy}{dx}$$
Thus we have
$$ 2x+2y \frac{dy}{dx}=0$$
Solving the equation for $\frac{dy}{dx}$, we obtain
$$ y’=\frac{dy}{dx}=-\frac{x}{y}$$
NOTE: The expression $\frac{dy}{dx}=-\frac{x}{y}$ is the derivative in terms of both $x$ and $y$. If we want to express in terms of $x$, we only consider the functions $y$ given explicitly $y=\pm \sqrt{25-x^{2}}$.
More precisely,
- for $y=\sqrt{25-x^{2}}$, we have $\frac{dy}{dx}=-\frac{x}{y}=-\frac{x}{\sqrt{25-x^{2}}}$
- for $y=-\sqrt{25-x^{2}}$, we have $\frac{dy}{dx}=-\frac{x}{y}=\frac{x}{\sqrt{25-x^{2}}}$