The cross product \(\mathbf{a}\times \mathbf{b}\) has the geometric interpretations as below:
(1)The cross product \(\mathbf{a}\times \mathbf{b} \) is orthogonal to both \(\mathbf{a} \) and \(\mathbf{b} \).
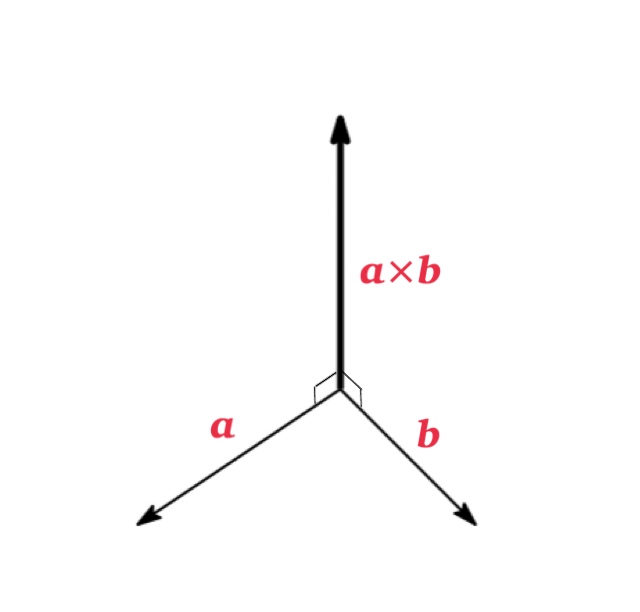
(2)The length of the cross product \(|\mathbf{a}\times \mathbf{b}| \) is equal to the area of parallelogram determined \(\mathbf{a} \) and \(\mathbf{b} \).
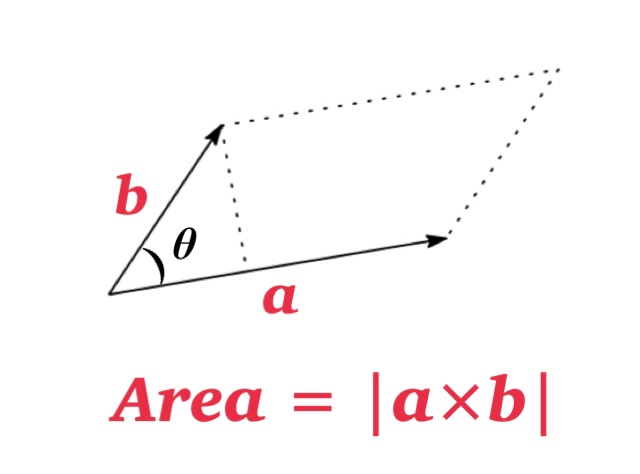
Proof of (1)
To prove that \(\mathbf{a}\times \mathbf{b}\) is orthogonal to \(\mathbf{a}\) and \(\mathbf{b}\), we show the computation \((\mathbf{a}\times \mathbf{b})\cdot \mathbf{a}=0\) and \((\mathbf{a}\times \mathbf{b})\cdot \mathbf{b}=0\).
$$\begin{eqnarray*}(\mathbf{a}\times \mathbf{b})\cdot \mathbf{a}&=&\left|\begin{array}{cc}a_{2}& a_{3}\\ b_{2}& b_{3}\end{array}\right|a_{1}-\left|\begin{array}{cc}a_{1}& a_{3}\\b_{1}& b_{3}\end{array}\right|a_{2}+\left|\begin{array}{cc}a_{1}& a_{2}\\ b_{1}& b_{2}\end{array}\right|a_{3}\\&=&a_{1}(a_{2}b_{3}-a_{3}b_{2})-a_{2}(a_{1}b_{3}-a_{3}b_{1})+a_{3}(a_{1}b_{2}-a_{2}b_{1})\\&=&0\end{eqnarray*}$$
Therefore, \(\mathbf{a}\times \mathbf{b}\) is orthogonal to \(\mathbf{a}\).
Similarly, we can show the computation \((\mathbf{a}\times \mathbf{b})\cdot \mathbf{b}=0\).
Example:
One of the properties of cross product \(\mathbf{a}\times \mathbf{b}=-\mathbf{b}\times \mathbf{a}\) can be seen easily by this description :
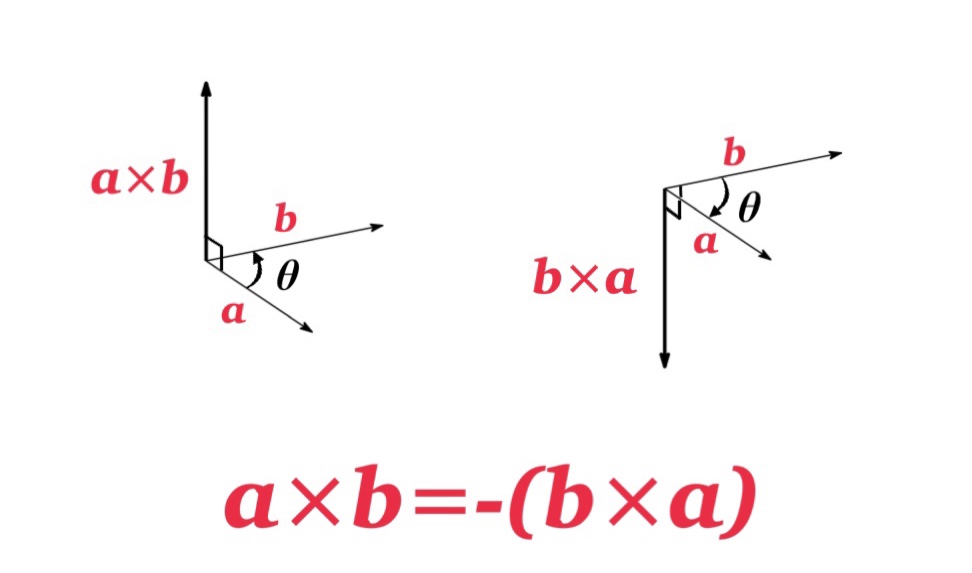
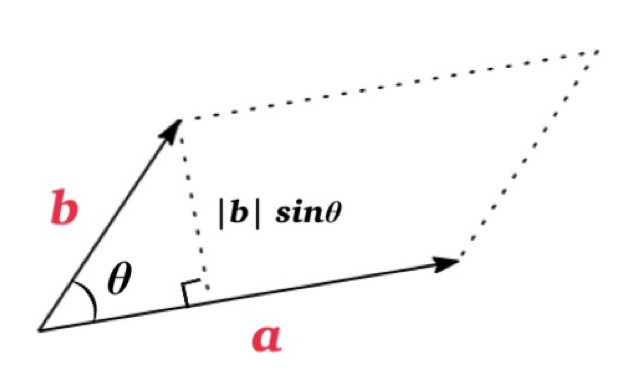
Proof of (2)
If \(\mathbf{a}\) and \(\mathbf{b}\) are represented by directed line segments with the same initial point as shown in Figure, then they determine a parallelogram with base \(|\mathbf{a}|\) and altitude \(|\mathbf{b}|\sin \theta\), and the area is given by
$$\text{Area}=|\mathbf{a}| \times (|\mathbf{b}|\sin \theta)=|\mathbf{a}\times \mathbf{b}|$$
See also Proof of \(|\mathbf{a}\times \mathbf{b}|=|\mathbf{a}| \times (|\mathbf{b}|\sin \theta)\).
Example: Find the area of the parallelogram determined by \(\mathbf{a}=(1,2,3)\) and \(\mathbf{b}=(4,5,6)\)
Solution:
$$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}&\ \mathbf{j}&\ \mathbf{k}\\1& 2& 3\\4& 5& 6\end{array}\right|=\left|\begin{array}{cc}2& 3\\ 5& 6\end{array}\right|\mathbf{i}-\left|\begin{array}{cc}1& 3\\4& 6\end{array}\right|\mathbf{j}+\left|\begin{array}{cc}1& 2\\ 4& 5\end{array}\right|\mathbf{k}=-3\mathbf{i}+6\mathbf{j}-3\mathbf{k}$$
Therefore the are of the parallelogram is the length of this cross product:
$$|\mathbf{a}\times \mathbf{b}|=\sqrt{(-3)^{2}+(6)^{2}+(-3)^{2}}=3\sqrt{6}$$