\(f(x)\) is an odd function if \(f(-x)=-f(x)\) for all \(x\) in its domain.
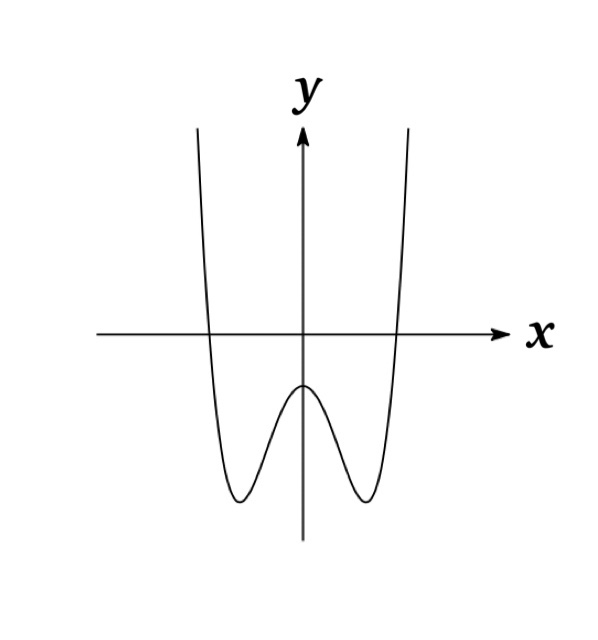
The graph of an even function is symmetric about the y-axis. Therefore if we have plotted the graph of \(f\) for \(x\geq 0\), we can obtain the entire graph by reflecting about the y-axis.
Example 1 : \(f(x)=x^{4}-3x^{2}-1\) is even since \(f(-x)=(-x)^{4}-3(-x)^{2}-1=x^{4}-3x^{2}-1=f(x)\).
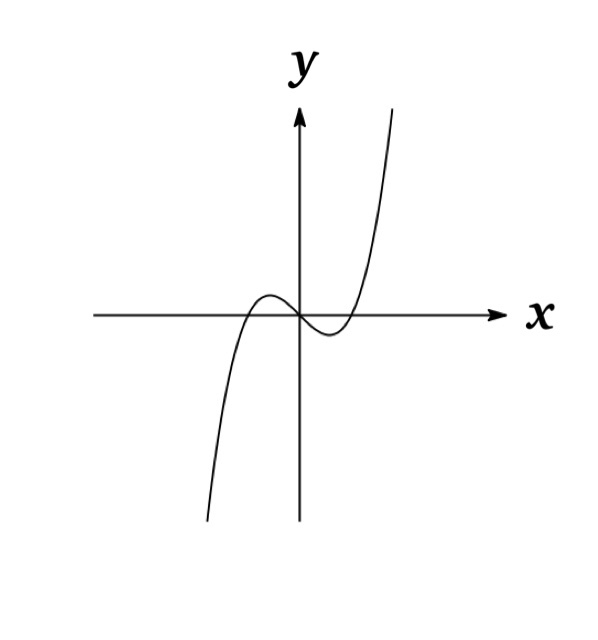
The graph of an odd function is symmetric about the origin. Therefore if we have plotted the graph of \(f\) for \(x\geq 0\), we can obtain the entire graph by rotating through \(180^{\circ}\) about the origin.
Example 2 : \(g(x)=x^{3}-x\) is odd since \(g(-x)=(-x)^{3}-(-x)=-x^{3}+x=-g(x)\).
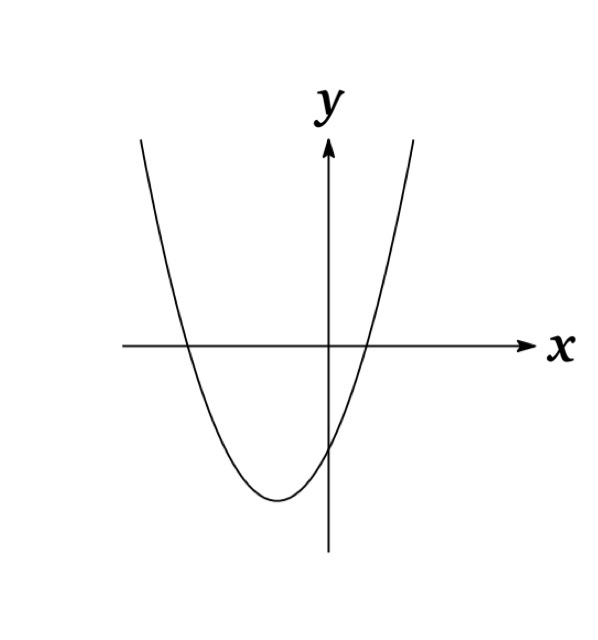
Notice that there are graphs such that the graphs are symmetric but not symmetric neither about the y-axis nor about the origin. Then the graphs are neither even nor odd.
Example 3 : \(h(x)=x^{2}+2x-2\) is neither even nor odd since \(h(-x)\not=h(x)\) and \(h(-x)\not=-h(x)\) where \(h(-x)=(-x)^{2}-2(-x)-2=x^{2}+2x-2\).
Contents
Addition and Multiplication
We denote even functions as (even) and odd functions as (odd) in below.
Addition
| (even)+(even)=(even) | |
| (odd)+(odd)=(odd) |
Multiplication
| (even)×(even)=(even) | |
| (even)×(odd)=(odd) | |
| (odd)×(odd)=(Even) |
These can be proved easily by the definition. We only prove the case of (odd)×(odd)=(Even). The others can be proved similarly.
Suppose \(f(x)\) and \(g(x)\) be odd functions. Then we have \(f(x)=-f(-x)\) and \(g(x)=-g(-x)\). Thus we obtain
$$f(x)g(x)=(-f(-x))(-g(-x))=f(-x)g(-x)$$
Integrals
Proof
First we decompose the integration interval :
$$\int_{-a}^{a} f(x)\ dx=\int_{-a}^{0} f(x)\ dx+\int_{0}^{a} f(x)\ dx$$
If let \(x=-t\), then by the Substitution Rue, the first term is given as below :
$$\int_{-a}^{0} f(x)\ dx=\int_{a}^{0} f(-t)(-1)\ dt=\int_{0}^{a} f(-t)\ dt$$
Then
\begin{eqnarray*}\text{even : } &&\int_{-a}^{0} f(x)\ dx=\int_{0}^{a} f(-t)\ dt=\int_{0}^{a} f(t)\ dt\\\text{odd : } &&\int_{-a}^{0} f(x)\ dx=\int_{0}^{a} f(-t)\ dt=-\int_{0}^{a} f(t)\ dt\\\end{eqnarray*}
Thus we obtain
$$\int_{-a}^{a} f(x)\ dx=\begin{cases}2\int_{0}^{a} f(x)\ dx & (\ f(x) : \text{even fun} )\\ & \\0 & (\ f(x) : \text{odd fun} )\end{cases}$$
Example
Find \(\int_{-1}^{1} (1+3x^{3}+4x^{4}+5x^{5}+6x^{6})\ dx\).
Solution : To make the calculation simple, we decompose into the sum of even and odd functions :
\begin{eqnarray*}\int_{-1}^{1} (1+3x^{3}+4x^{4}+5x^{5}+6x^{6})\ dx&=&\int_{-1}^{1} (1+4x^{4}+6x^{6})\ dx+\int_{-1}^{1} (3x^{3}+5x^{5})\ dx\\&=&2\int_{0}^{1} (1+4x^{4}+6x^{6})\ dx+0\\&=&2[x+\frac{4}{5}x^{5}+\frac{6}{7}x^{7}]_{0}^{1}\\&=&\frac{186}{35}\end{eqnarray*}
Property
Any function can be decomposed into the sum of even and odd functions.
We can prove the above by using the identity \(X=\frac{X+Y}{2}+\frac{X-Y}{2}\).
Proof
Any function f(x) can be composed as
$$f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}$$
Then \(f_{1}(x):=\frac{f(x)+f(-x)}{2}\) is even since \(f_{1}(-x)=f_{1}(x)\) and \(f_{2}(x):=\frac{f(x)-f(-x)}{2}\) is odd since \(f_{2}(-x)=-f_{2}(x)\).
Example
Exponential function \(\mathrm{e}^{x}\) can be composed as
$$\mathrm{e}^{x}=\frac{\mathrm{e}^{x}+\mathrm{e}^{-x}}{2}+\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{2}$$
The RHS of the equation is called hyperbolic functions. Especially, the first term \(\frac{\mathrm{e}^{x}+\mathrm{e}^{-x}}{2}\) is denoted by \(\cosh x\) and the second term \(\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{2}\) is denoted by \(\sinh x\).