Let \(\theta\) be any real number. Then Euler’s formula state that
$$\mathrm{e}^{i\theta}=\cos \theta+i\sin \theta $$
where \(\mathrm{e}\) is the base of the natural logarithm and \(i\) is the imaginary unit.
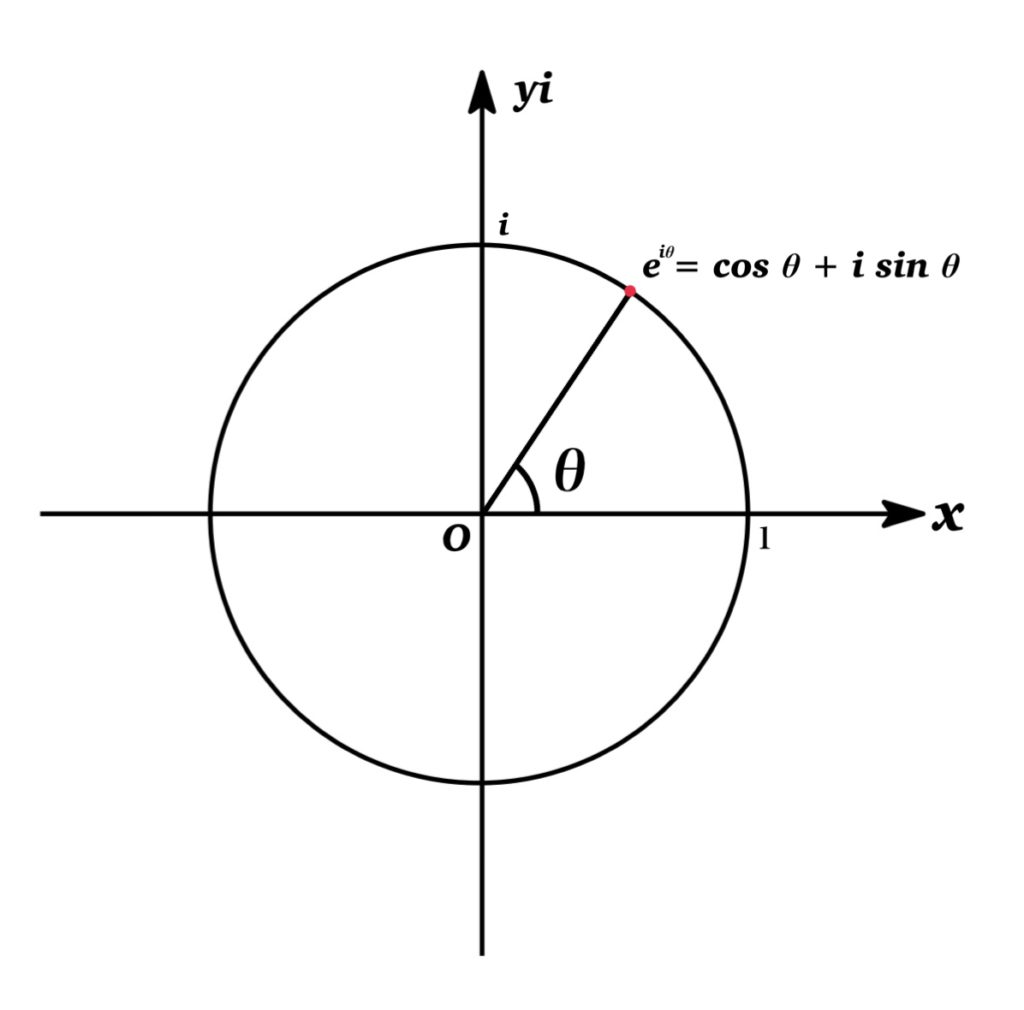
Notice that \(\mathrm{e}^{i\theta}\) lie on the circle of radius 1 rotated by angle \(\theta\) in the complex plane as shown in figure, and Euler’s equation provides us with easier method of De Moivre’s Theorem:
$$(\cos \theta+i\sin \theta)^{n}=(\mathrm{e}^{i\theta})^{n}=\mathrm{e}^{i(n\theta)}=\cos n\theta+i\sin n\theta$$
Contents
Examples
Applying Euler’s formula with \(\theta=\frac{\pi}{2},\ \pi,\ 2\pi\), we have
- \(\mathrm{e}^{i \frac{\pi}{2}}=\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}=0+i(1)=i\)
- \(\mathrm{e}^{i \pi}=\cos \pi+i \sin \pi=-1+i (0)=-1\)
- \(\mathrm{e}^{i 2\pi}=\cos 2\pi+i \sin 2\pi=1+i (0)=1\)
Proof
Using the Taylor series for \(\mathrm{e}^{x},\ \cos \theta\) and \(\sin \theta\), we have
$$\begin{eqnarray*}\mathrm{e}^{x}&=&1+\frac{1}{1!}x^{}+\frac{1}{2!}x^{2}+\cdots +\frac{1}{k!}x^{k}+\cdots\\\sin \theta&=&\theta-\frac{1}{3!}\theta^{3}+\frac{1}{5!}\theta^{5}-\cdots +\frac{(-1)^{k}}{(2k+1)!}\theta^{2k+1}+\cdots\\\cos \theta&=&1-\frac{1}{2!}\theta^{2}+\frac{1}{4!}\theta^{4}-\cdots +\frac{(-1)^{k}}{(2k)!}\theta^{2k}+\cdots\end{eqnarray*}$$
If we put \(x=i\theta\) where \(\theta\) is a real number in equation of \(\mathrm{e}^{x}\), we get
$$\begin{eqnarray*}\mathrm{e}^{i\theta}&=&1+i\theta+\frac{1}{2!}{(i\theta)}^{2}+\frac{1}{3!}(i\theta)^{3}+\frac{1}{4!}(i\theta)^{4}\cdots +\frac{1}{k!}{(i\theta)}^{k}+\cdots\\&=&1+i\theta-\frac{1}{2!}\theta^{2}-\frac{1}{3!}i\theta^{3}+\frac{1}{4!}\theta^{4}+\cdots\\&=&\left(1-\frac{1}{2!}\theta^{2}+\frac{1}{4!}\theta^{4}-\cdots\right)+i\left(\theta-\frac{1}{3!}\theta^{3}+\frac{1}{5!}\theta^{5}-\cdots \right)\\&=&\cos \theta+i\sin \theta\end{eqnarray*}$$
Remark
By using Euler’s formula, the trigonometric functions can be expressed in terms of \(\mathrm{e}\) as below: $$\sin x=\frac{\rm{e}^{ix}-\rm{e}^{-ix}}{2i}\ \ \ \ \ \cos x=\frac{\rm{e}^{ix}+\rm{e}^{-ix}}{2}$$
These equations are derived by using Euler’s formula :
- \(\mathrm{e}^{ix}=\cos x+i\sin x\)
- \(\mathrm{e}^{-ix}=\cos x-i\sin x \)
Second equation is given by substituting -x for x in Euler’s formula.
By the two equations above, we have
- \(\mathrm{e}^{ix}+\mathrm{e}^{-ix}=2\cos x\)
- \(\mathrm{e}^{ix}-\mathrm{e}^{-ix}=2i\sin x\)
Therefore, we obtain
- \(\sin x=\frac{\rm{e}^{ix}-\rm{e}^{-ix}}{2i}\)
- \(\cos x=\frac{\rm{e}^{ix}+\rm{e}^{-ix}}{2}\)
Especially, the form \(\frac{e^{x}-e^{-x}}{2}\) and \(\frac{e^{x}+e^{-x}}{2}\) are known as hyperbolic functions:
- \(\sinh x=\frac{e^{x}-e^{-x}}{2}\) ( hyperbolic sine )
- \(\cosh x=\frac{e^{x}+e^{-x}}{2}\) ( hyperbolic cosine )
Therefore the trigonometric functions are expressed in terms of hyperbolic functions as follows : $$\sin x=-i\sinh ix\ \ \ \ \ \cos x=\cosh ix$$
From these relational expressions, it is natural that trigonometric functions and hyperbolic functions have similar properties. There are some differences in sign, but the differences are due to the imaginary unit “i”.