$y=f(x)$ を 原点を中心に 「x 軸方向に a 倍」, 「 y 軸方向に b 倍」拡大・縮小した方程式は$$\frac{y}{b}=f\left(\frac{x}{a}\right)$$で表される.
グラフを $x$ 軸に $a$ 倍とは, $y=f(x)$ 上の各点 $(x,y)$ を $(ax, y)$ にうつす変換を指す.
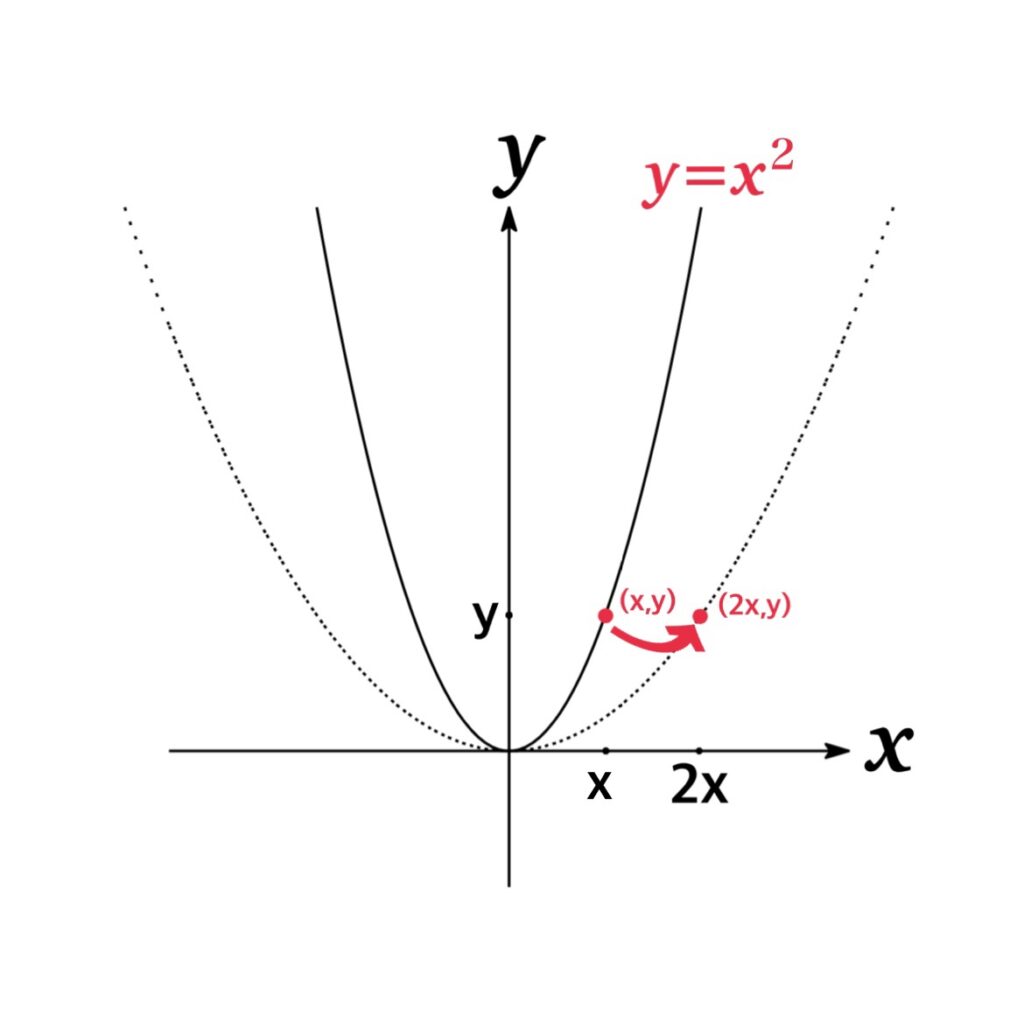
例えば, $y=x^{2}$ のグラフを $x$ 方向に $2$ 倍する拡大では $(1,1)$ が$(2,1)$, $(2,4)$ が $(4,4)$, $(3,9)$ が $(6,9)$ ・・・ に移り全体としては $y=\left(\frac{x}{2}\right)^{2}=\frac{x^{2}}{4}$ という関数になる.
証明 : $y=f(x)$上の任意の点 $(x,y)$ を 原点を中心に 「x 軸方向に a 倍」, 「 y 軸方向に b 倍」した点を $(X,Y)$ とする.
このとき $X=a\cdot x,\ Y=b\cdot y$ で表されるので
$$x=\frac{X}{a},\ y=\frac{Y}{b}$$
となる. このとき、 $(X,Y)$ が満たす関係式を求めればよいので
$$\frac{Y}{b}=f(\frac{X}{a})$$
が求めたい方程式である.
・$a>1$ のとき、拡大 (bについても同様)
・$0< a <1$ のとき、 縮小 (bについても同様)
・$a=-1$ のとき、 $y=f(-x)$ となり y 軸に関する対称移動
・$b=-1$ のとき、 $y=-f(x)$ となり x 軸に関する対称移動
・$a=-1, b=-1$ のとき、 $y=-f(-x)$ となり 原点に関する対称移動
例
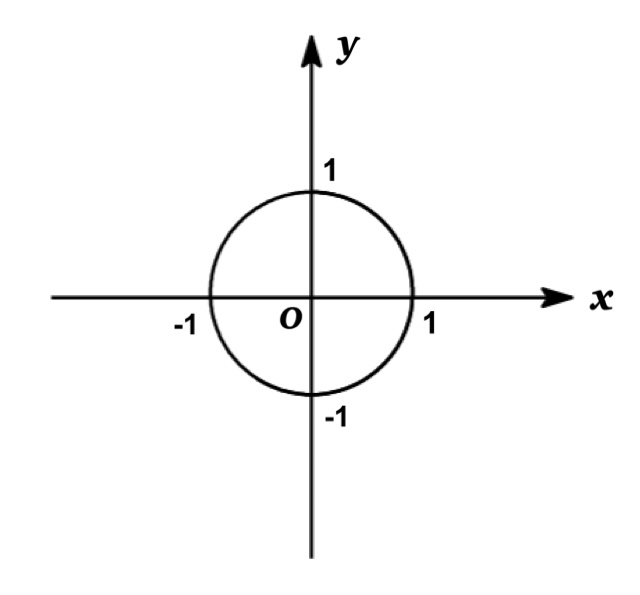
$x^{2}+y^{2}=1$ を 「x 軸方向に a 倍」, 「y 軸方向に b 倍」だけ拡大・縮小したグラフの関数を求めよ.
x 軸方向に a 倍, y 軸方向に b 倍だけ拡大・縮小するので求めたい方程式は次のように表わされる.
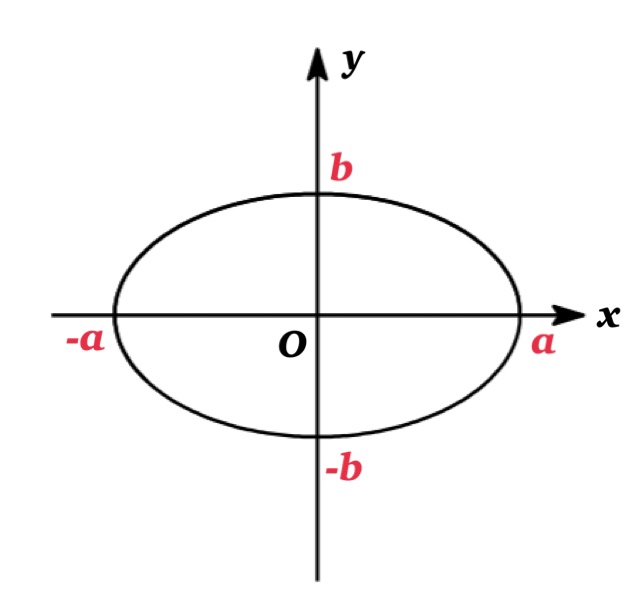
$$\left(\frac{x}{a}\right)^{2}+ \left(\frac{y}{b}\right)^{2}=1$$
よって $a\not =b$ の場合, 円を x 軸方向に a 倍, y 軸方向に b 倍したものは楕円となる.