任意の正整数 n に対して
$$(\cos \theta+i\sin \theta)^{n}=\cos n\theta+i\sin n\theta$$
複素数 の $n$ 乗は, 複素数を 極形式 で表し, ド・モアブルの定理を利用して計算すれば良い.
幾何的解釈
複素数 $z=\cos \theta+i\sin \theta$ の表す点は, 原点を中心とする半径 $1$ の円周上にある. このとき複素数 $z$ に $z^{n-1}$ をかけた $z^{n}$ は, $z$ を原点まわりに角 $(n-1)\theta$ だけ回転させた点を表す.
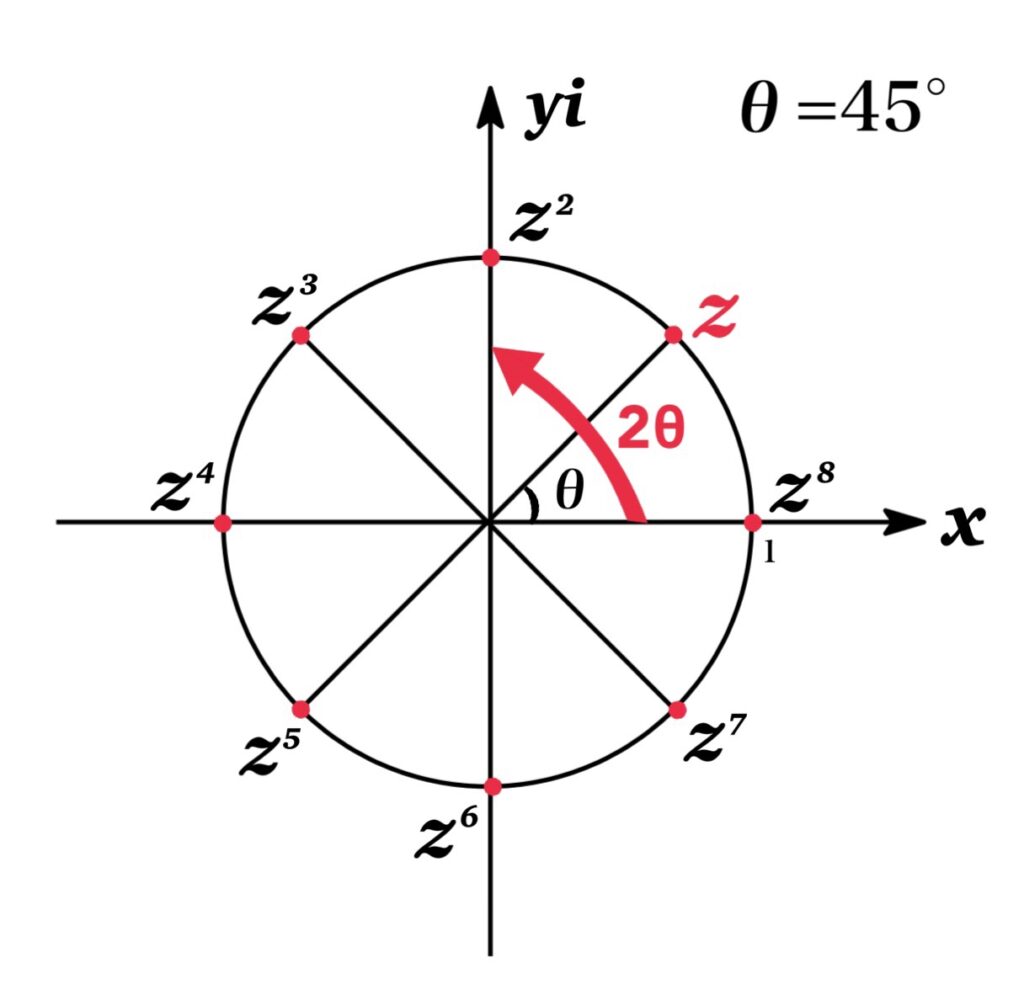
一般に, 複素数 $z=r(\cos\theta+\sin\theta)$ に対して $n$ を整数とするとき, 次が成り立つ.
$$[r(\cos \theta+i\sin \theta)]^{n}=r^{n}(\cos n\theta+i\sin n\theta)$$
Contents
例
$(-1+\sqrt{3}i)^{10}$ を求めよ.
$(-1+\sqrt{3}i)=2(\cos 120^{\circ}+i\sin 120^{\circ})$ より
\begin{eqnarray*}(-1+\sqrt{3}i)^{10}&=&2^{10}(\cos 1200^{\circ}+i\sin 1200^{\circ})\\&=&1024(\cos 120^{\circ}+i\sin 120^{\circ})\ \ \ (\text{ ∵ } 1200^{\circ}=120^{\circ}+360^{\circ}\times 3)\\&=&1024\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\&=&-512+512\sqrt{3}i\end{eqnarray*}
証明
帰納法による証明:
$z=\cos \theta+i\sin \theta$ とおく.
n=2 のとき
$$\begin{eqnarray*}z^{2}&=&(\cos \theta+i\sin \theta)(\cos \theta+i\sin \theta)\\&=&(\cos^{2}\theta-\sin^{2}\theta)+i(2\sin\theta\cos\theta)\ ( \text{∵加法定理})\\&=&\cos 2\theta+i\sin 2\theta\end{eqnarray*}$$
n=k のとき
$z^{k}=(\cos \theta+i\sin \theta)^{k}=\cos k\theta+i\sin k\theta$ が成立すると仮定.
$$\begin{eqnarray*}z^{k+1}&=&z^{k}\cdot z\\&=&(\cos k\theta+i\sin k\theta)(\cos \theta+i\sin \theta)\\&=&(\cos k\theta\cos\theta-\sin k\theta\sin\theta)+i(\sin k\theta\cos\theta+\cos k\theta\sin\theta)\ (\text{∵加法定理})\\&=&\cos (k+1)\theta+i\sin (k+1)\theta\end{eqnarray*}$$
となり $n=k+1$ のときも定理は成立する.
よって、数学的帰納法により定理が証明された.
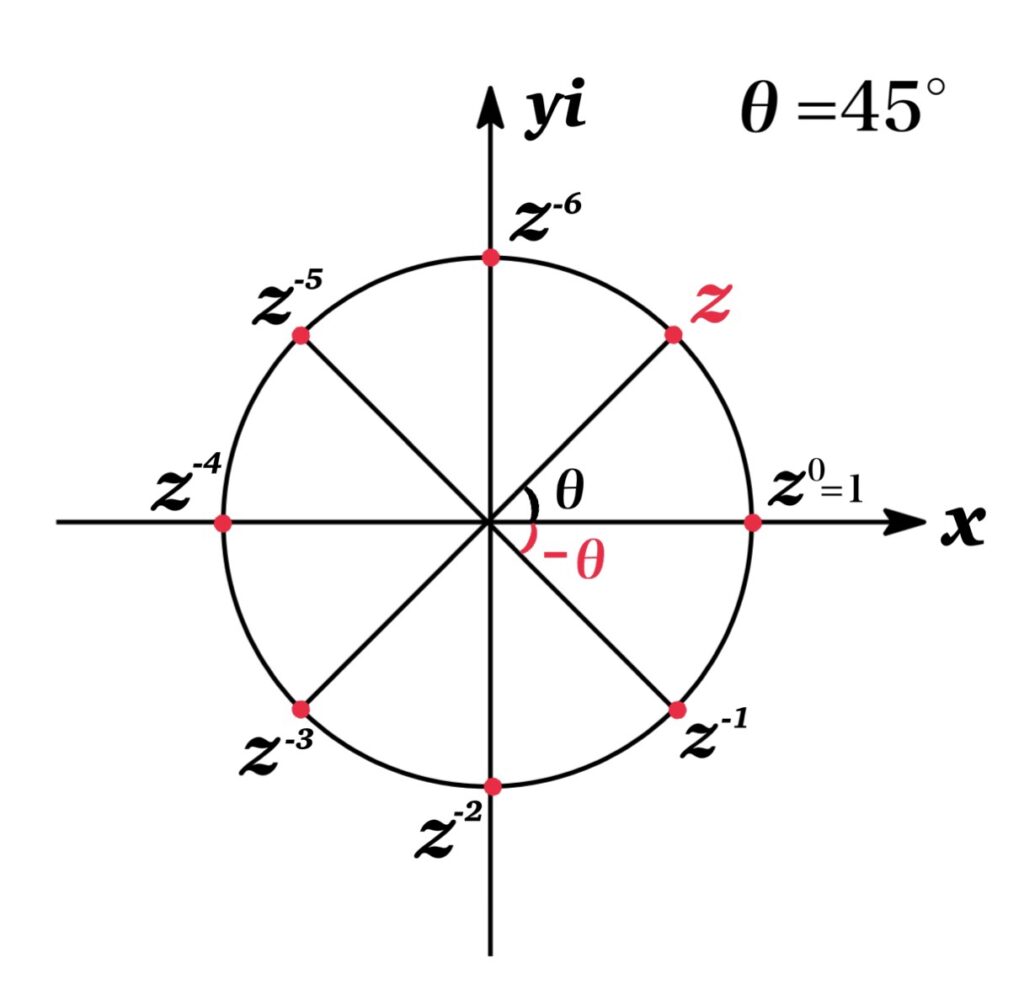
n が負の整数の場合
n=-m ( m は正整数) の場合も ド・モアブルの定理が成り立つことを示す.
$$\begin{eqnarray*}z^{-m}&=&(\cos \theta+i\sin \theta)^{-m}\\&=&\frac{1}{(\cos \theta+i\sin \theta)^{m}}\\&=&\frac{1}{\cos m\theta+i\sin m\theta}\\&=&\frac{\cos m\theta-i\sin m\theta}{(\cos m\theta+i\sin m\theta)(\cos m\theta-i\sin m\theta)}\\&=&\cos m\theta-i\sin m\theta\\&=&\cos (-m\theta)+i\sin (-m\theta)\\\end{eqnarray*}$$
よって n が負の整数の場合もド・モアブルの定理が成立する.
また $z^{0}=1$ と定義するれば, 任意の整数 $n$ に対してド・モアブルの定理が成立する.
例
$(-\sqrt{3}+i)^{-4}$ を求めよ.
$(-\sqrt{3}+i)=2(\cos 150^{\circ}+i\sin 150^{\circ})$ より
\begin{eqnarray*}(-\sqrt{3}+i)^{-4}&=&2^{-4}(\cos (150\times (-4))^{\circ}+i\sin (150\times (-4))^{\circ})\\&=&\frac{1}{16}(\cos (-600) ^{\circ}+i\sin (-600)^{\circ})\\&=&\frac{1}{16}(\cos 120^{\circ}+i\sin 120^{\circ}) \ \ \ (\text{ ∵ } -600^{\circ}=120^{\circ}+360^{\circ}\times (-2))\\&=&\frac{1}{16}\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\&=&-\frac{1}{32}+\frac{\sqrt{3}}{32}i\end{eqnarray*}