For any positive integer n and any real number \(\theta\) $$(\cos \theta+i\sin \theta)^{n}=\cos n\theta+i\sin n\theta$$
The \(n\)th root of a complex number can be calculated by expressing the complex number in polar form and using De Moivre’s theorem.
Notice that a complex number written in polar form \(z=\cos \theta+i\sin \theta\) lie on the circle of radius 1 in the complex plane.
Then the geometric interpretation of the nth power of a complex number \(z\) represents the point where \(z\) is rotated around the origin by an angle \((n-1)\theta\).
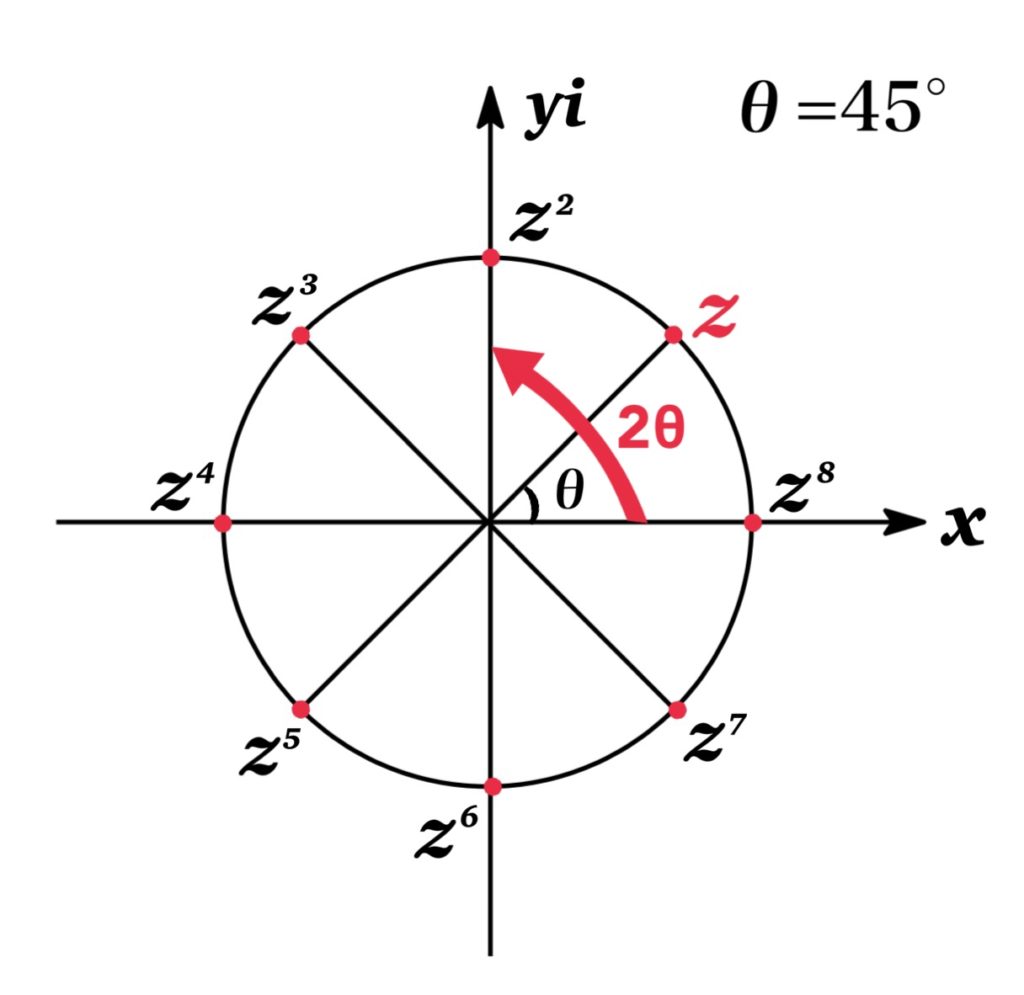
In general, if \(z=r(\cos\theta+\sin\theta)\) and \(n\) is a integer,
$$[r(\cos \theta+i\sin \theta)]^{n}=r^{n}(\cos n\theta+i\sin n\theta)$$
Example
Find \((-1+\sqrt{3}i)^{10}\).
Since \((-1+\sqrt{3}i)=2(\cos 120^{\circ}+i\sin 120^{\circ})\), we obtain
\begin{eqnarray*}(-1+\sqrt{3}i)^{10}&=&2^{10}(\cos 1200^{\circ}+i\sin 1200^{\circ})\\&=&1024(\cos 120^{\circ}+i\sin 120^{\circ})\ \ \ (\text{ ∵ } 1200^{\circ}=120^{\circ}+360^{\circ}\times 3)\\&=&1024\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\&=&-512+512\sqrt{3}i\end{eqnarray*}
Proof by induction
Let \(z=\cos \theta+i\sin \theta\).
Then, the statement is true for n=2 since
$$\begin{eqnarray*}z^{2}&=&(\cos \theta+i\sin \theta)(\cos \theta+i\sin \theta)\\&=&(\cos^{2}\theta-\sin^{2}\theta)+i(2\sin\theta\cos\theta)\ (\text{by Multiple-angle formula})\\&=&\cos 2\theta+i\sin 2\theta\end{eqnarray*}$$
Suppose that the statement is true for n=k:
$$z^{k}=(\cos \theta+i\sin \theta)^{k}=\cos k\theta+i\sin k\theta.$$
Then
\begin{eqnarray*}z^{k+1}&=&z^{k}\cdot z\\&=&(\cos k\theta+i\sin k\theta)(\cos \theta+i\sin \theta)\\&=&(\cos k\theta\cos\theta-\sin k\theta\sin\theta)+i(\sin k\theta\cos\theta+\cos k\theta\sin\theta)\ (\text{by Multiple-angle formula})\\&=&\cos (k+1)\theta+i\sin (k+1)\theta\end{eqnarray*}
Thus the statement is true for all positive integer n.
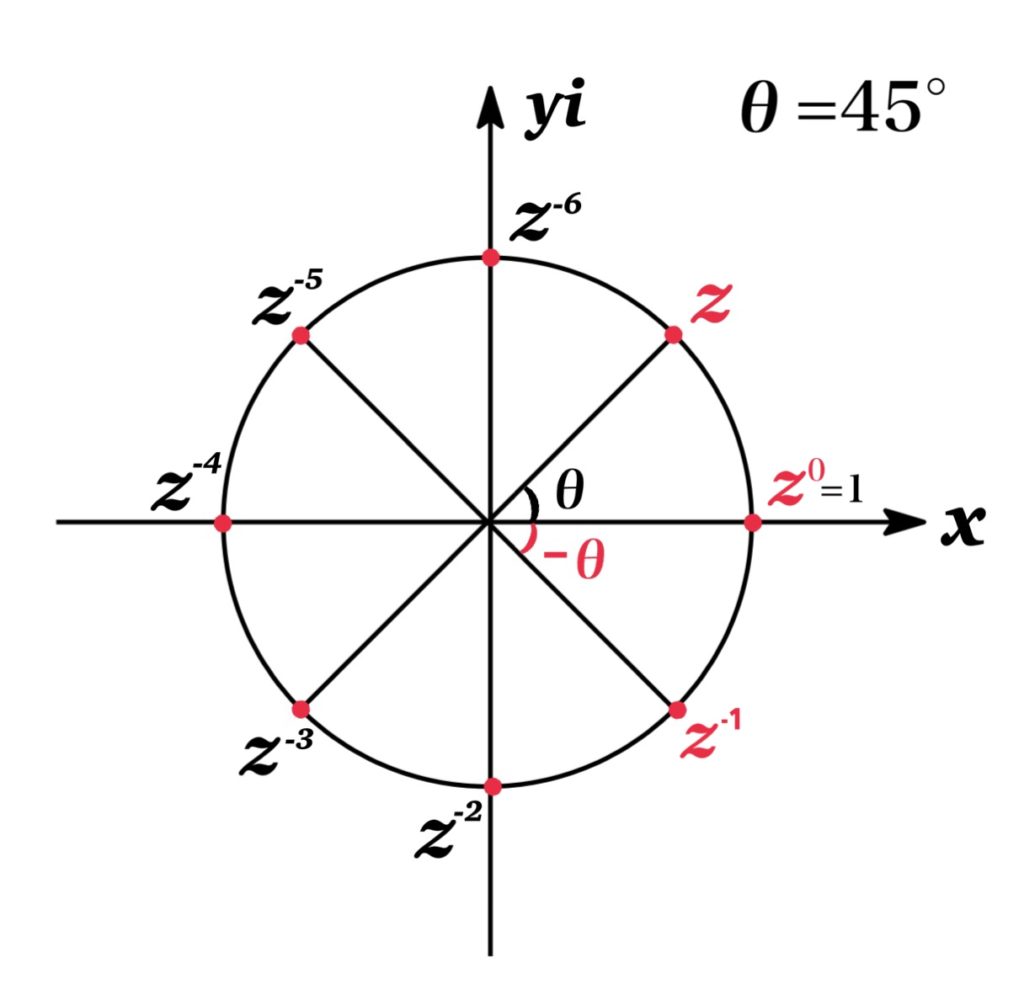
For any negative interger -m
For any negative integer \(-m\) $$(\cos \theta+i\sin \theta)^{-m}=\cos (-m\theta)+i\sin (-m\theta)$$
We extend the De Moivre’s Theorem in the case of a negative integer -m.
$$\begin{eqnarray*}z^{-m}&=&(\cos \theta+i\sin \theta)^{-m}\\&=&\frac{1}{(\cos \theta+i\sin \theta)^{m}}\\&=&\frac{1}{\cos m\theta+i\sin m\theta}\\&=&\frac{\cos m\theta-i\sin m\theta}{(\cos m\theta+i\sin m\theta)(\cos m\theta-i\sin m\theta)}\\&=&\cos m\theta-i\sin m\theta\\&=&\cos (-m\theta)+i\sin (-m\theta)\\\end{eqnarray*}$$
Thus, De Moivre’s Theorem is true for any negative integer -m.
Furthermore, if we define \(z^{0}=(\cos \theta+i\sin \theta)^{0}=1\), the De Moivre’s Theorem is true for m=0. Therefore De Moivre’s Theorem is true for any integers.
Example
Find \((-\sqrt{3}+i)^{-4}\) .
Since \((-\sqrt{3}+i)=2(\cos 150^{\circ}+i\sin 150^{\circ})\), we obtain
\begin{eqnarray*}(-\sqrt{3}+i)^{-4}&=&2^{-4}(\cos (150\times (-4))^{\circ}+i\sin (150\times (-4))^{\circ})\\&=&\frac{1}{16}(\cos (-600) ^{\circ}+i\sin (-600)^{\circ})\\&=&\frac{1}{16}(\cos 120^{\circ}+i\sin 120^{\circ}) \ \ \ (\text{ ∵ } -600^{\circ}=120^{\circ}+360^{\circ}\times (-2))\\&=&\frac{1}{16}\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\&=&-\frac{1}{32}+\frac{\sqrt{3}}{32}i\end{eqnarray*}