Let X and Y be random variables. Then the covariance of X and Y is defined by
$$\sigma_{XY}=Cov[X, Y]=E[(X-\overline{X})(Y-\overline{Y})]$$
where $\overline{X}$ and $\overline{Y}$ are the means or expectations of $X$ and $Y$.
Covariance is one of the quantities representing the relationship between the random variables. The sign of the covariance shows the tendency in the linear relationship.
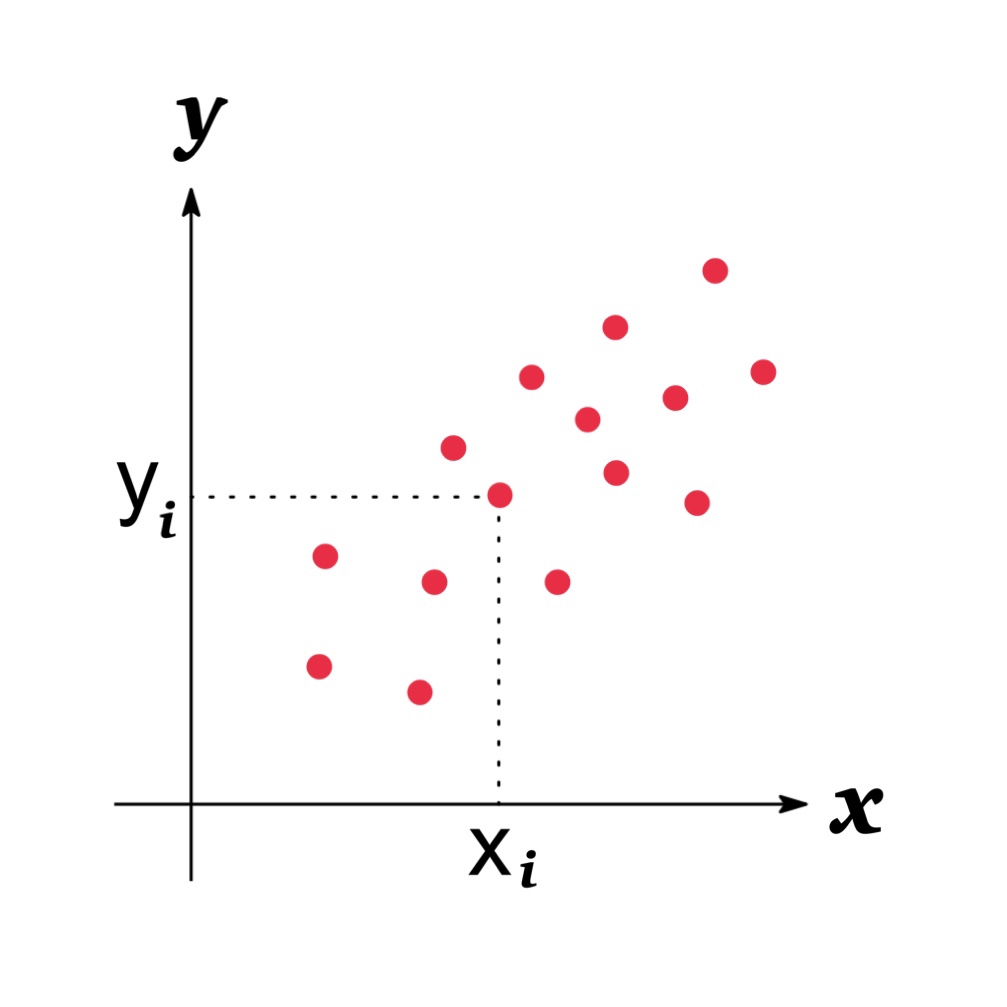
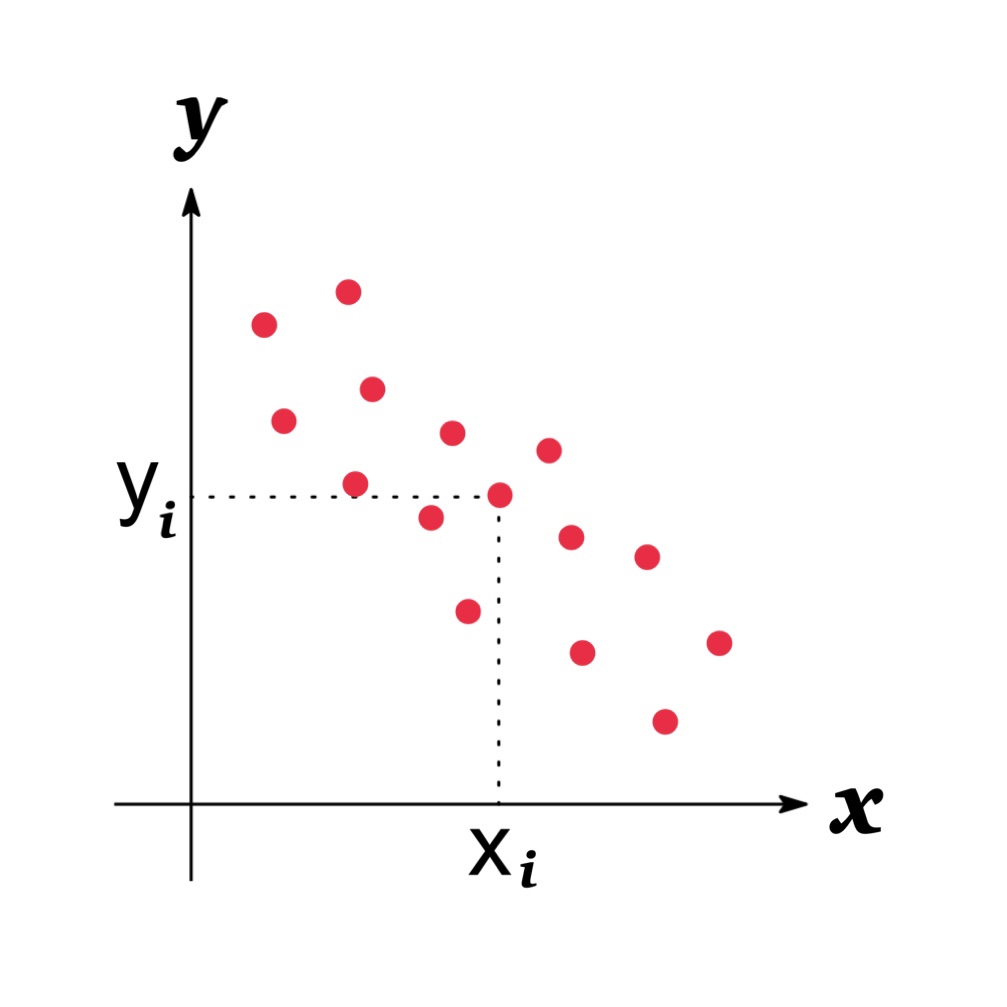
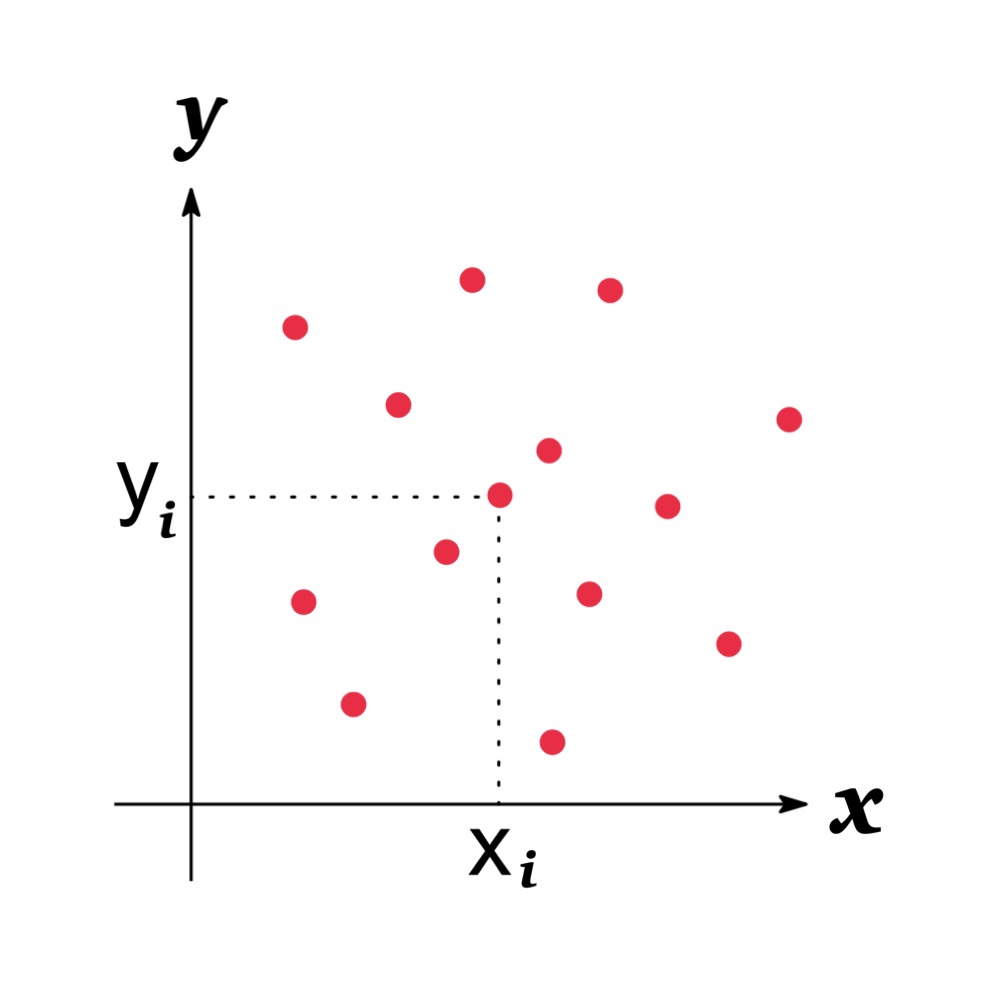
The covariance of $X$ and $Y$, $Cov[X, Y]$, has the following properties:
- If $Cov[X,Y]>0$, $Y$ tends to increase (or decrease) as $X$ increases (or decrease).
- If $Cov[X, Y]<0$, $X$ tends to decrease (or increase) as $X$ increases (or decrease).
- If there is no relationship indicated above between the variables, $Cov[X, Y]\approx 0$.
This can be explained by using a scatter diagram.
In the scatter diagram, the more scattered in the regions ② and ③, the more the two variables tend to move in the same direction, and the covariance value takes a positive value, indicating a positive correlation.
On the other hand, the more scattered in regions ① and ④, the more the two variables tend to move in opposite directions, and the covariance value takes a negative value, indicating a negative correlation.
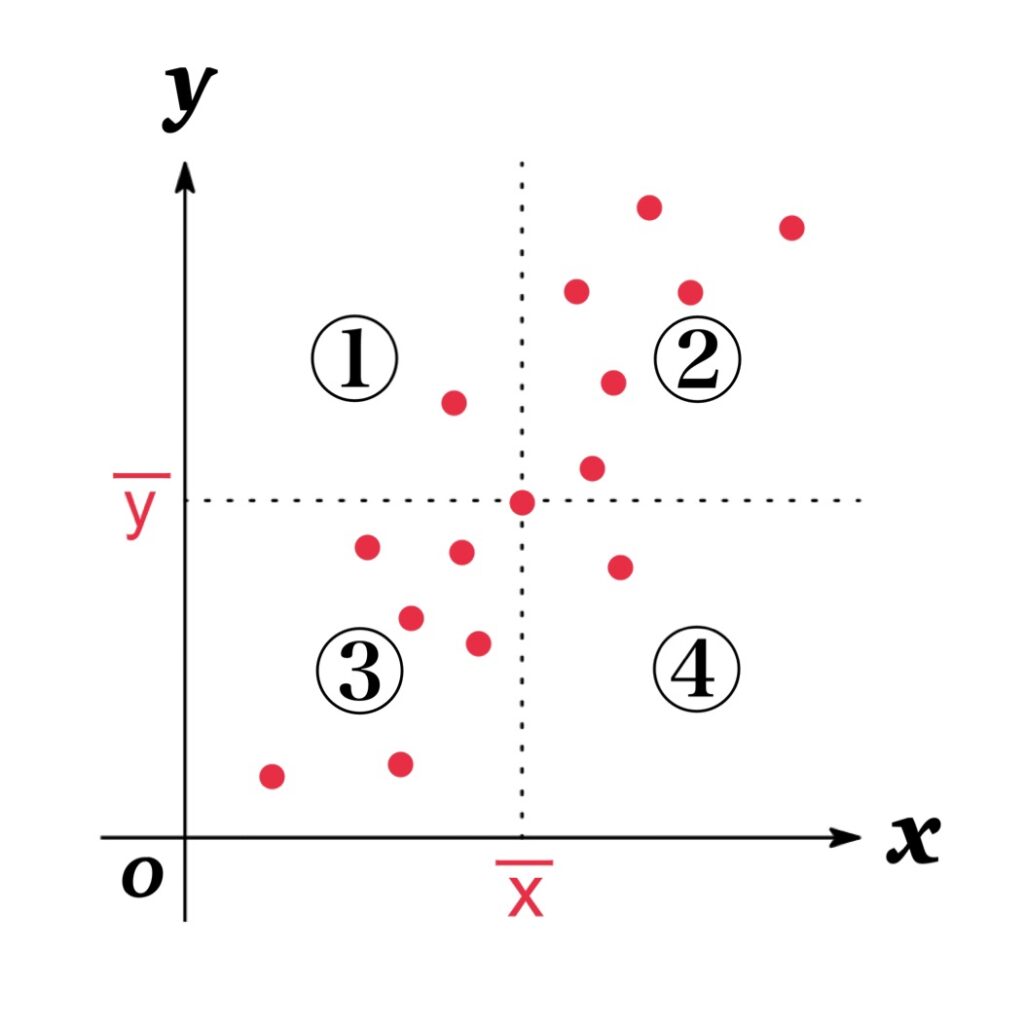
- ① $(x_{i}-\overline{x})(y_{i}-\overline{y})<0$
- ②$(x_{i}-\overline{x})(y_{i}-\overline{y})>0$
- ③$(x_{i}-\overline{x})(y_{i}-\overline{y})>0$
- ④$(x_{i}-\overline{x})(y_{i}-\overline{y})<0$
NOTE : If $X=Y$, we have
$$Cov[X, X]=E[\left(X-E[X]\right)(X-E[X])]=V[X]$$
and this is equivalent to the variance of $X$.
Discrete / Continuous Case
Let \(f(x,y)\) be the joint probability function. And also let \(E[X]=\mu_{X}\) and \(E[Y]=\mu_{Y}\). Then the covariance of X and Y are give by
\begin{eqnarray*}Cov[X, Y]&=&\sum_{x}\sum_{y}\ (x-\mu_{X})(y-\mu_{Y})\cdot f(x, y) \ \ \ \ \ \ \ \ \ \text{(discrete variable)}\\Cov[X, Y]&=&\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\ (x-\mu_{X})(y-\mu_{Y})\cdot f(x, y)\ dxdy\ \ \ \ \text{(continuous variable)}\end{eqnarray*}
where expectation or mean \(E[X]=\mu_{X}\) is given as below:
\begin{eqnarray*}E[X]=\mu_{X}&=&\sum_{x}\sum_{y}\ x\cdot f(x, y) \ \ \ \ \ \ \ \ \ \text{(discrete variable)}\\E[X]=\mu_{X}&=&\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\ x\cdot f(x, y)\ dxdy\ \ \ \ \text{(continuous variable)}\end{eqnarray*}
Properties
| \(Cov[X, Y]=E[XY]-E[X]E[Y]\) | Proof |
| \(V[aX+bY]=a^{2}V[X]+2abCov[X,Y]+b^{2}V[Y]\) | Proof |
| $Cov[X, X]=E[\left(X-E[X]\right)(X-E[X])]=V[X]$ | |
| $Cov[X,Y]=Cov[Y,X]$ | |
| $Cov[X, a]=0$ | |
| $Cov[aX, bY]=ab\ Cov[X,Y]$ | |
| $Cov[X+a,Y+b]=Cov[X,Y]$ | |
| $Cov[aX+bY, cW+dV]=ac\ Cov[X,W]+ad\ Cov[X,V]+bc\ Cov[Y,W]+bd\ Cov[Y,V]$ | |
| If X and Y are independent, $$Cov[X, Y]=E[XY]-E[X]E[Y]=0$$ |