Let $n$ be a positive integer. Then Binomial Theorem states that
$$(x+y)^{n}=\displaystyle\sum_{k=0}^{n} \left(\begin{array}{c}n\\k\end{array}\right) x^{n-k}y^{k}$$
This theorem is the generalization of $(x+y),\ (x+y)^{2},\ (x+y)^{3},\cdots$, and states that the coefficient of $x^{n-k}y^{k}$ when we expand $(x+y)^{n}$ is given by $x^{n-k}y^{k}$. For example, if we expand $(x+y)^{3}$, the coefficient of $x^{2}y^{1}$ is given by $\left(\begin{array}{c}3\\1\end{array}\right)=3$.
| Expansion | $\left(\begin{array}{c}n\\k\end{array}\right)$ Notation | |
| $(x+y)^{1}=x+y$ | \((x+y)^{1}=\left(\begin{array}{c}1\\0\end{array}\right)x^{1}y^{0}+\left(\begin{array}{c}1\\1\end{array}\right)x^{0}y^{1}\) | |
| $(x+y)^{2}=x^{2}y+2xy+y^{2}$ | $(x+y)^{2}=\left(\begin{array}{c}2\\0\end{array}\right)x^{2}y^{0}+\left(\begin{array}{c}2\\1\end{array}\right)x^{1}y^{1}+\left(\begin{array}{c}2\\2\end{array}\right)x^{0}y^{2}$ | |
| $(x+y)^{3}=x^{3}+3x^{2}y+3xy^{2}+y^{3}$ | $(x+y)^{3}=\left(\begin{array}{c}3\\0\end{array}\right)x^{3}y^{0}+\left(\begin{array}{c}3\\1\end{array}\right)x^{2}y^{1}+\left(\begin{array}{c}3\\2\end{array}\right)x^{1}y^{2}+\left(\begin{array}{c}3\\3\end{array}\right)x^{0}y^{3}$ |
$$\left(\begin{array}{c}n\\k\end{array}\right)=\frac{n\cdot (n-1)\cdots (n-k+1)}{k!}=\frac{n!}{k!(n-k)!}$$
with a positive integer \(k \leq n\).
And also, when \(k=0\), we define
$$\left(\begin{array}{c}n\\0\end{array}\right)=1, \ \ x^{0}=y^{0}=1$$
Remark $\left(\begin{array}{c}n\\k\end{array}\right)$ represents the number of combinations that $k$ things taken from $n$ and $\left(\begin{array}{c}n\\k\end{array}\right)$ is also denoted by ${}_{n} C_{k}$.
Properties
| $\left(\begin{array}{c}n\\k\end{array}\right)=\left(\begin{array}{c}n\\n-k\end{array}\right)$ | Proof |
| $\left(\begin{array}{c}n-1\\k-1\end{array}\right)+\left(\begin{array}{c}n-1\\k\end{array}\right)=\left(\begin{array}{c}n\\k\end{array}\right)$ | Proof |
| $k\times \left(\begin{array}{c}n\\k\end{array}\right)=n\times \left(\begin{array}{c}n-1\\k-1\end{array}\right)$ | Proof |
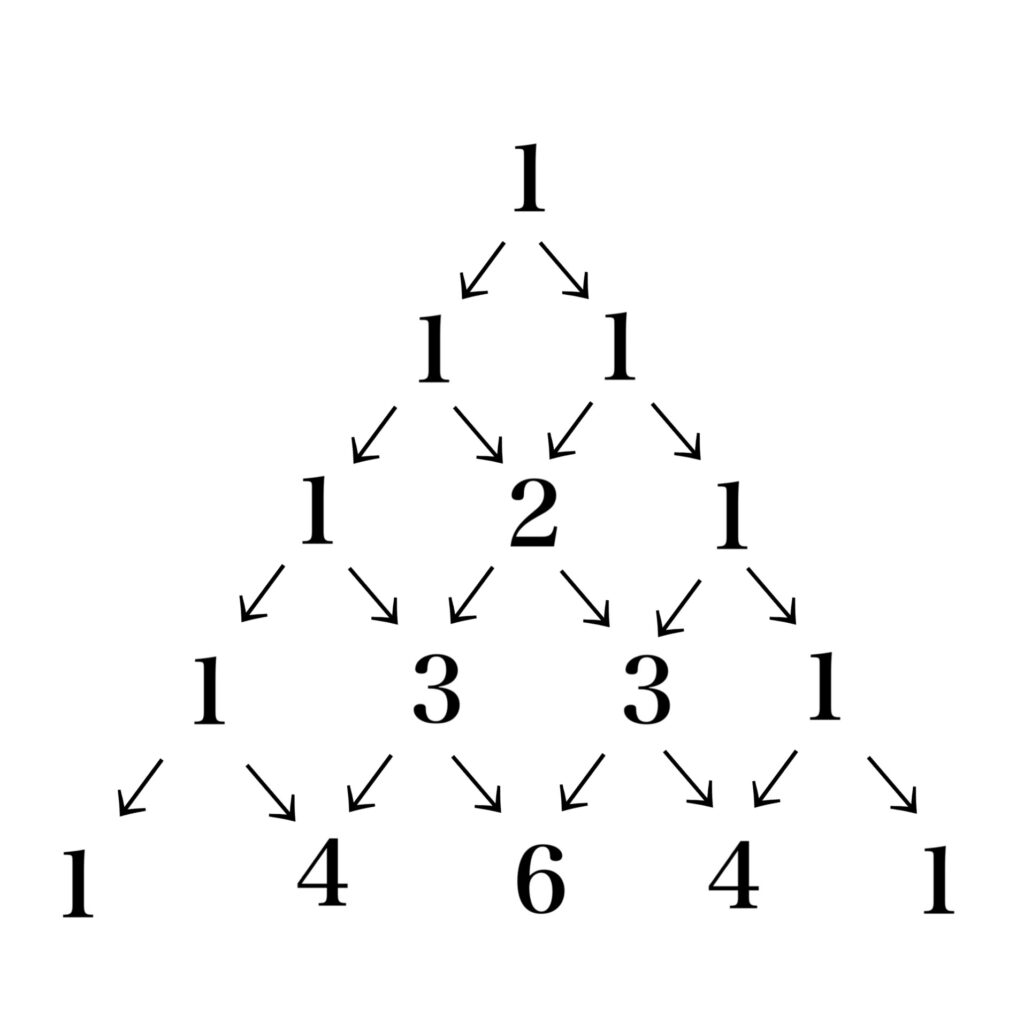
Pascal’s Triangle
Every number in Pascal’s triangle is the sum of two numbers in the previous row, one directly above it and the other just to the left.
Also, since the property of binomial coefficient:
$$\left(\begin{array}{c}n-1\\k-1\end{array}\right)+\left(\begin{array}{c}n-1\\k\end{array}\right)=\left(\begin{array}{c}n\\k\end{array}\right)$$
Pascal’s Triangle coincidence with the coefficients of expanded binomial of the form $(x+y)^{n}$.

Negative Binomial Theorem
Binomial Theorem holds for a negative integer $-n$: $$(x+y)^{-n}=\displaystyle\sum_{k=0}^{\infty} \left(\begin{array}{c}-n\\k\end{array}\right) x^{k}y^{-n-k}=\displaystyle\sum_{k=0}^{\infty} (-1)^{k} \left(\begin{array}{c}n+k-1\\k\end{array}\right) x^{k}y^{-n-k}$$ and the identity is called the negative binomial theorem.
The negative binomial theorem is expanded to the case in which n is negative.
Notice that the negative binomial coefficient \(\left(\begin{array}{c}-n\\k\end{array}\right)\)is defined by
$$\left(\begin{array}{c}-n\\k\end{array}\right)=\frac{-n\cdot (-n-1)\cdots (-n-k+1)}{k!}$$
and since \((-n)\cdot (-n-1)\cdots (-n-k+1)=(-1)^{k}(n+k-1)\cdots(n+1)\cdot (n)\),
$\left(\begin{array}{c}-n\\k\end{array}\right)$ can be rewrite as
$$\left(\begin{array}{c}-n\\k\end{array}\right)=(-1)^{k}\left(\begin{array}{c}n+k-1\\k\end{array}\right)$$
Example
Expand $\frac{1}{(1+x)^{2}}$ as a power series.
Solution : Since ${}_{-2} C_{k}=(-1)^{k} {}_{2+k-1}C_{k}=(-1)^{k} (k+1)$, we have
\begin{eqnarray*}\frac{1}{(1+x)^{2}}&=&(1+x)^{-2}=\displaystyle\sum_{k=0}^{\infty}{}_{-2} C_{k} x^{k}\\&=&\displaystyle\sum_{k=0}^{\infty}(-1)^{k}(k+1) x^{k}\\&=&1-2x+3x^{2}-4x^{3}+5x^{4}-6x^{5}+\cdots \end{eqnarray*}