The nth partial sums of the Taylor series
$$f_{n}(x):=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f”(a)}{2!}(x-a)^{2}+\cdots +\frac{f^{n}(a)}{n!}(x-a)^{n}$$
is a polynomial of degree n and called the nth-degree Taylor polynomial of f at a.
Notice that \(f_{n}(x)\) is the approximation of the function by a Taylor polynomial of degree n.
(In the case of a=0, the Taylor polynomials at 0 is called the Maclaurin polynomials.)
Therefore, as n increases, \(f_{n}(x)\) becomes a better approximation to \(f(x)\) and it is true that
$$\displaystyle\lim_{n\rightarrow \infty} f_{n}(x)=f(x)$$
Example
For the exponential function $f(x)=\mathrm{e}^{x}$, the Taylor polynomials at $0$ (Maclaurin polynomials) with $n=1, 2,$ and $3$ are given by
$$f_{1}(x)=1+x,\ \ f_{2}(x)=1+x+\frac{x^{2}}{2!}, \ \ f_{3}(x)=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}$$
The graph of the exponential function and there three Taylor polynomials are shown as below:

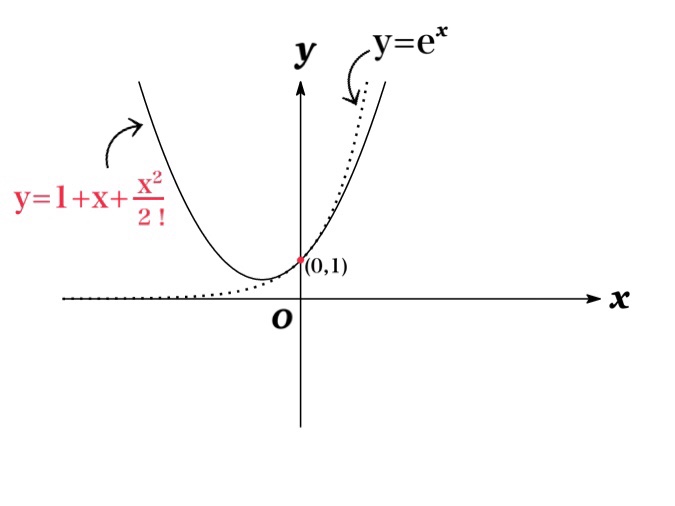

The graphs show that $f_{n}(x)$ appears to approach $\mathrm{e}^{x}$ as $n$ increases.
Application to Calculation]
Approximate \((1.00005)^{17}\) by a first degree Taylor polynomial at \(a=0\) .
Let $$f(x)=(1+x)^{17}$$, then we have $$(1.00005)^{17}=(1+0.00005)^{17}=f(0.00005)$$
By a Taylor expansion at a=0, we have
$$f(x)=(1+x)^{17}=_{17}\mathrm{C}_{0}+_{17}\mathrm{C}_{1}x+_{17}\mathrm{C}_{2}x^{2}+\cdots +_{17}\mathrm{C}_{k}x^{k}+\cdots$$
Thus, the first degree Taylor polynomial is given by
$$f(x)=(1+x)^{17}\approx \ _{17}\mathrm{C}_{0}+_{17}\mathrm{C}_{1}x$$
and the desired approximation is
$$f(0.00005)=(1+0.0005)^{17}\approx \ _{17}\mathrm{C}_{0}+_{17}\mathrm{C}_{1} (0.00005)=1.00085$$
Approximate \(\sin 0.1\) by a Taylor polynomial of degree 3 at \(a=0\) .
Let \(f(x)=\sin x\), then we have \(\sin 0.1=f(0.1)\).
By a Taylor expansion at a=0, we have
$$f(x)=\sin x=x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\cdots +\frac{(-1)^{k}}{(2k+1)!}x^{2k+1}+\cdots$$
Thus, the 3rd degree Taylor polynomial is given by
$$f(x)=\sin x\approx \ x-\frac{1}{3!}x^{3}$$
and the desired approximation is
$$f(0.1)=\sin 0.1\approx \ 0.1-\frac{1}{3!}(0.1)^{3}=0.09983$$
First degree
We have known that the tangent line of $f$ at $(a, f(a))$ is given by
$$y=f(a)+f'(a)(x-a)$$
and that a curve lies very close to its tangent line near the point tangency.
Thus, we settle the tangent line at $(a, f(a))$ as a linear approximation to the curve $f(x)$ when $x$ is near $a$.
In fact, the tangent line is the same as the first degree Taylor polynomial:
$$f_{1}(x)=f(a)+f'(a)(x-a)$$
Note that this is an approximation, therefore error occurs.
