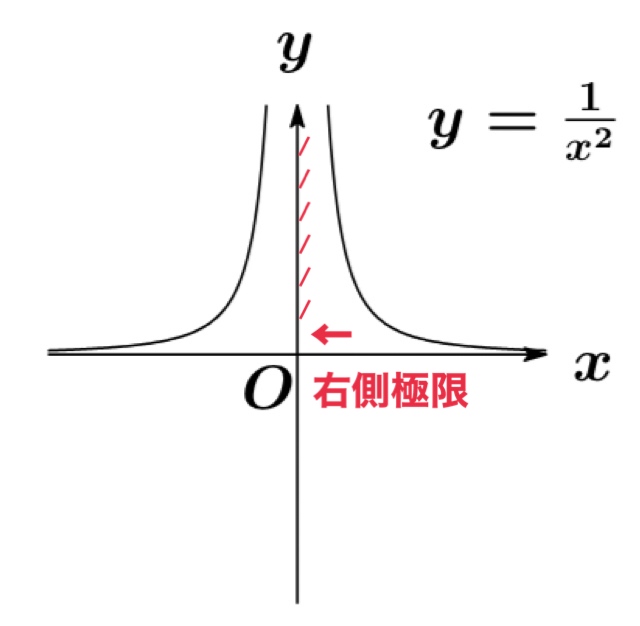
右側極限
\(x\)が\(a\)より大きい値から\(a\)に近づくことを \(x\rightarrow a+0\)で表す.
\(x\rightarrow a+0\)のとき, 関数\(f(x)\)の極限値を
$$\displaystyle\lim_{x\rightarrow a+0} f(x)$$
で表し, \(x=a\)における\(f(x)\)の右側極限値という.
なお、\(a=0\)の場合は簡略的に\(x\rightarrow +0\)と書き表す.
例題1
$x=1$ における $f(x)=\frac{x^{2}-1}{x-1}$ の右側極限を求めよ.
解答:$x=1$ のとき, $f(1)=\frac{1^{2}-1}{1-1}=\frac{0}{0}$ と不定形になっているので約分で式変形を行う.
$$\lim_{x\rightarrow 1+0}\frac{x^{2}-1}{x-1}=\lim_{x\rightarrow 1+0}\frac{(x+1)(x-1)}{x-1}=\lim_{x\rightarrow 1+0}\ x+1=2$$
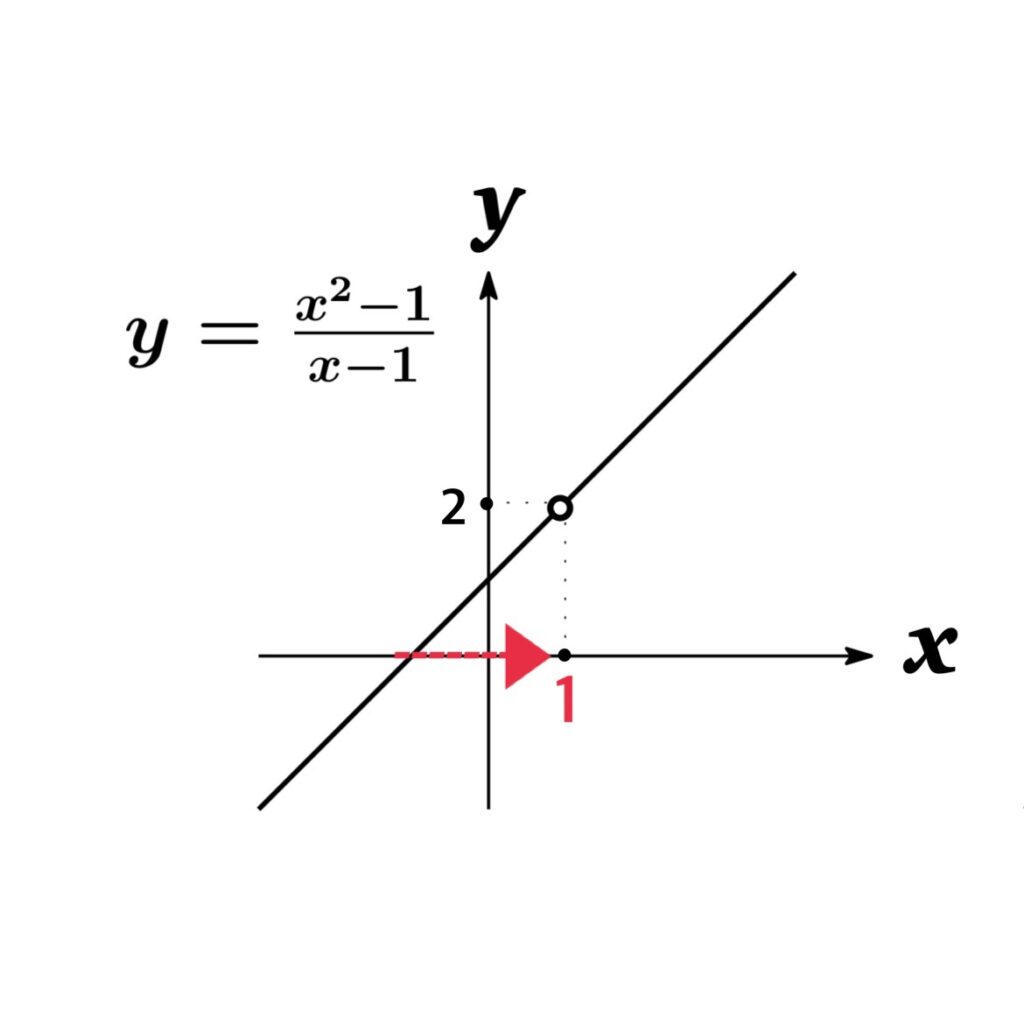
注意:ここで $x=1$における極限とは $x$ が $1$ と異なる値をとりながら 限りなく $1$ に近づくことであり, $x=1$における $f(x)$ の値ではない.
右側極限の場合, $x$ が $1$ より大きい値をとりながら $1$ に限りなく近づくことなので, $x=1.001,\ 1.0001,\ 1.00001,\ 1.000001,\cdots$ のように徐々に $x$ が右から $1$ に近づく場合に $f(x)$ の値が何に近づくのかを表している.
実際, $x=1$ において $f(x)=\frac{x-1}{x^{2}-1}$ は定義されていない.
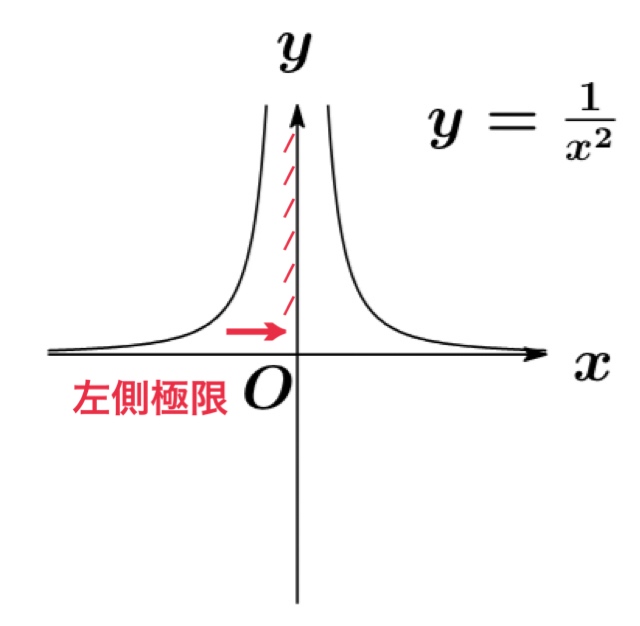
左側極限
\(x\)が\(a\)より小さい値から\(a\)に近づくことを \(x\rightarrow a-0\)で表す.
\(x\rightarrow a-0\)のとき, 関数\(f(x)\)の極限値を
$$\displaystyle\lim_{x\rightarrow a-0} f(x)$$
で表し, \(x=a\)における\(f(x)\)の左側極限値という.
なお、\(a=0\)の場合は簡略的に\(x\rightarrow -0\)と書き表す.
例題
$x=1$ における $f(x)=\frac{x^{2}-1}{x-1}$ の左側極限を求めよ.
解答:右側極限の場合と同様に $f(1)=\frac{1^{2}-1}{1-1}=\frac{0}{0}$ と不定形になっているので約分で式変形を行う.
$$\lim_{x\rightarrow 1-0}\frac{x^{2}-1}{x-1}=\lim_{x\rightarrow 1-0}\frac{(x+1)(x-1)}{x-1}=\lim_{x\rightarrow 1-0}\ x+1=2$$

注意:左側極限の場合, $x$ が $1$ より小さい値をとりながら $1$ に限りなく近づくことなので, $x=0.99,\ 0.999,\ 0.9999,\ 0.99999,\ \cdots $ のように $x$ が徐々に左から $1$ に近づく場合に $f(x)$ の値が何に近づくのかを表している.