$x$ が $a$ と異なる値を取りながら $f(x)$ が $A$ に近づくとき
$$\lim_{x\rightarrow a}f(x)=A$$
と表し, $A$ を $x\rightarrow a$ における $f(x)$ の極限値という.
極限値 $\lim_{x\rightarrow a}f(x)=A$ とは, 次の3つの条件を満たす必要がある.
- 右側極限 $\displaystyle\lim_{x\rightarrow a+0}f(x)$ が存在する.
- 左側極限 $\displaystyle\lim_{x\rightarrow a-0}f(x)$が存在する.
- 右側極限と左側極限の値が等しい:$\displaystyle\lim_{x\rightarrow a+0}f(x)=\displaystyle\lim_{x\rightarrow a-0}f(x)$
注意:ここで $x=a$における極限とは $x$ が $a$ と異なる値をとりながら 限りなく $a$ に近づくいたときの $f(x)$ の値であり, $x=a$における $f(x)$ の値ではない.
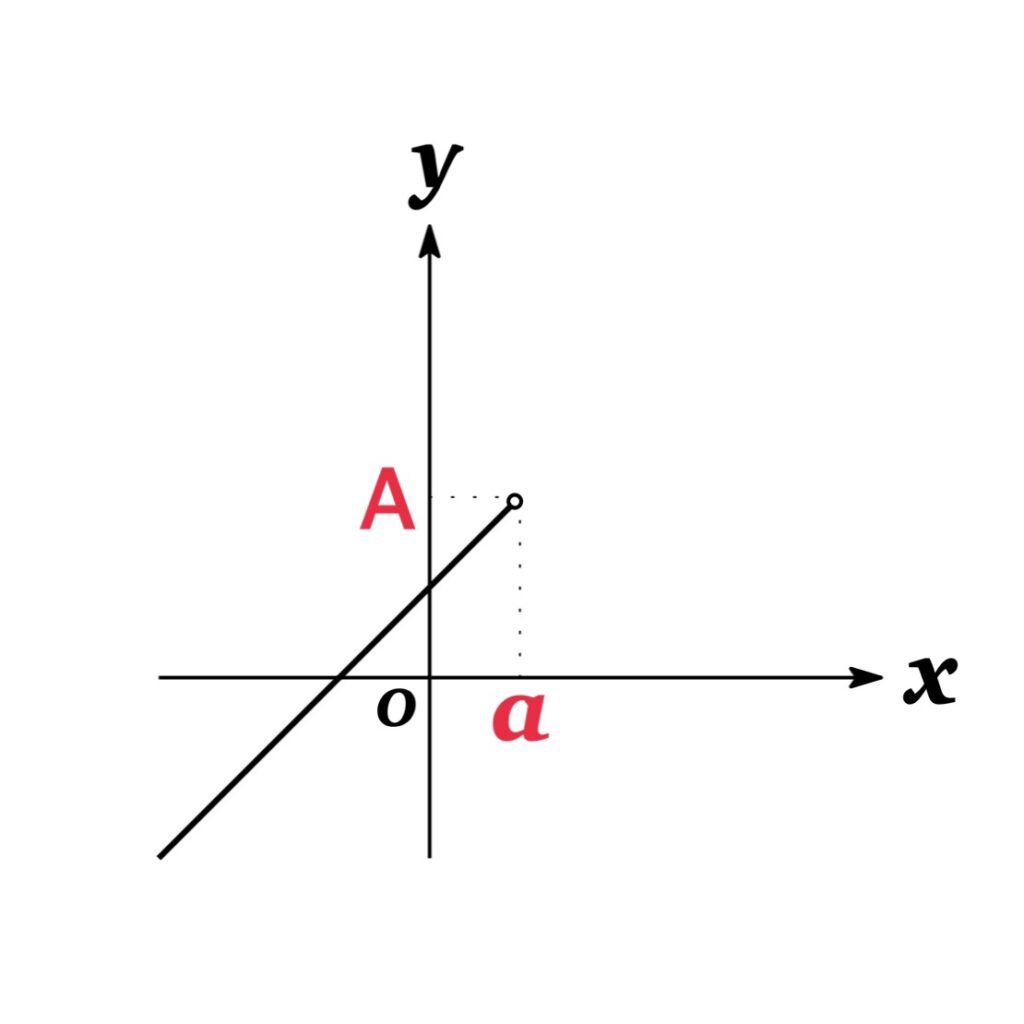
$\lim_{x\rightarrow a}f(x)=A$ となる例:
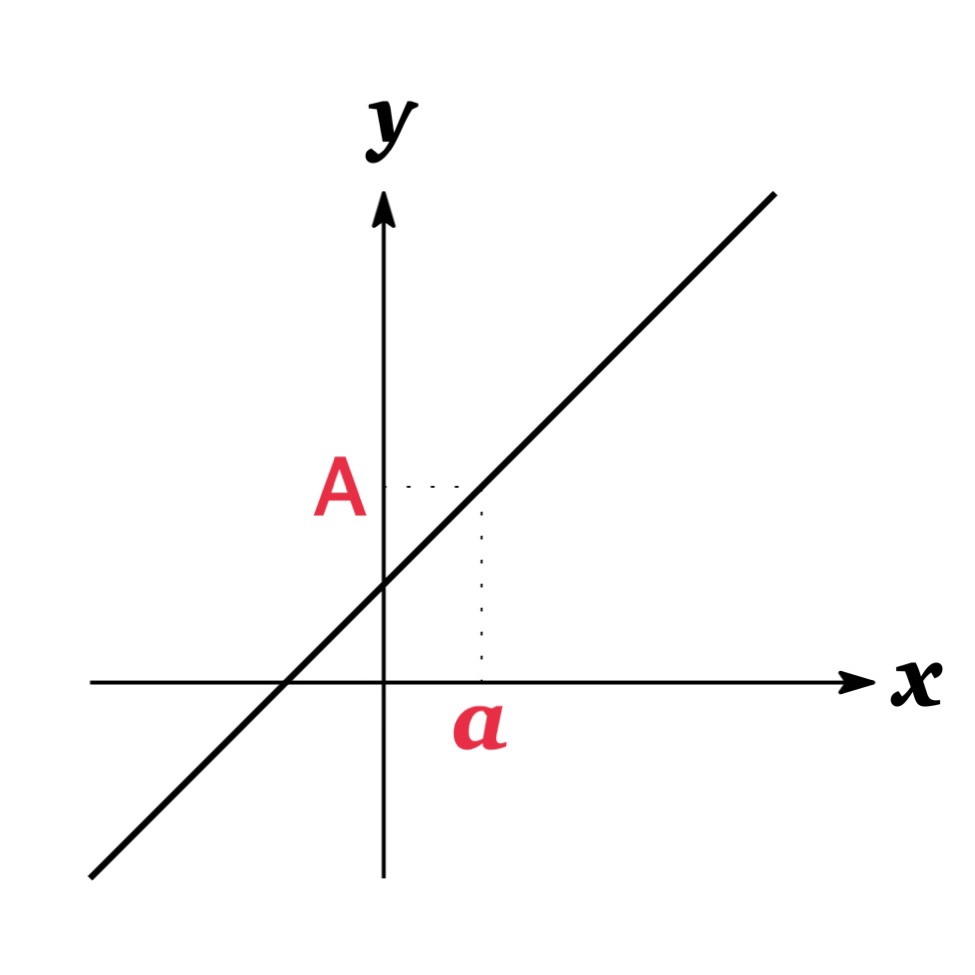
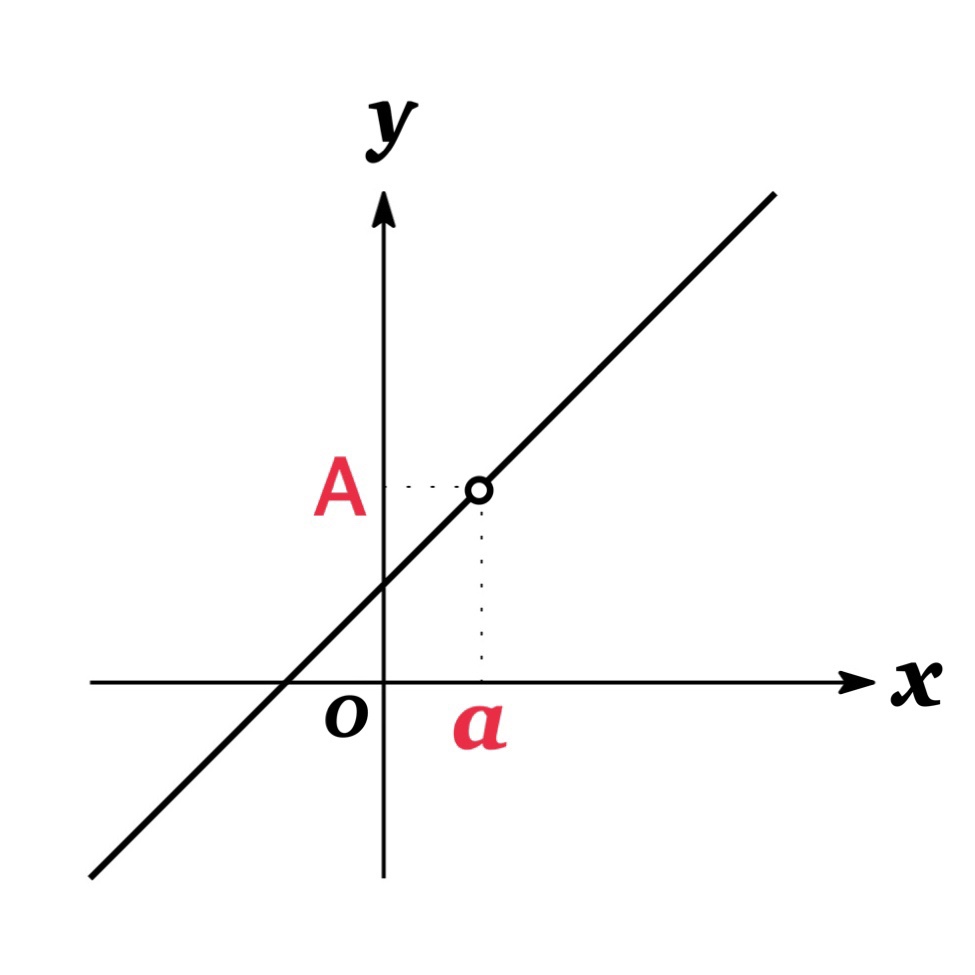
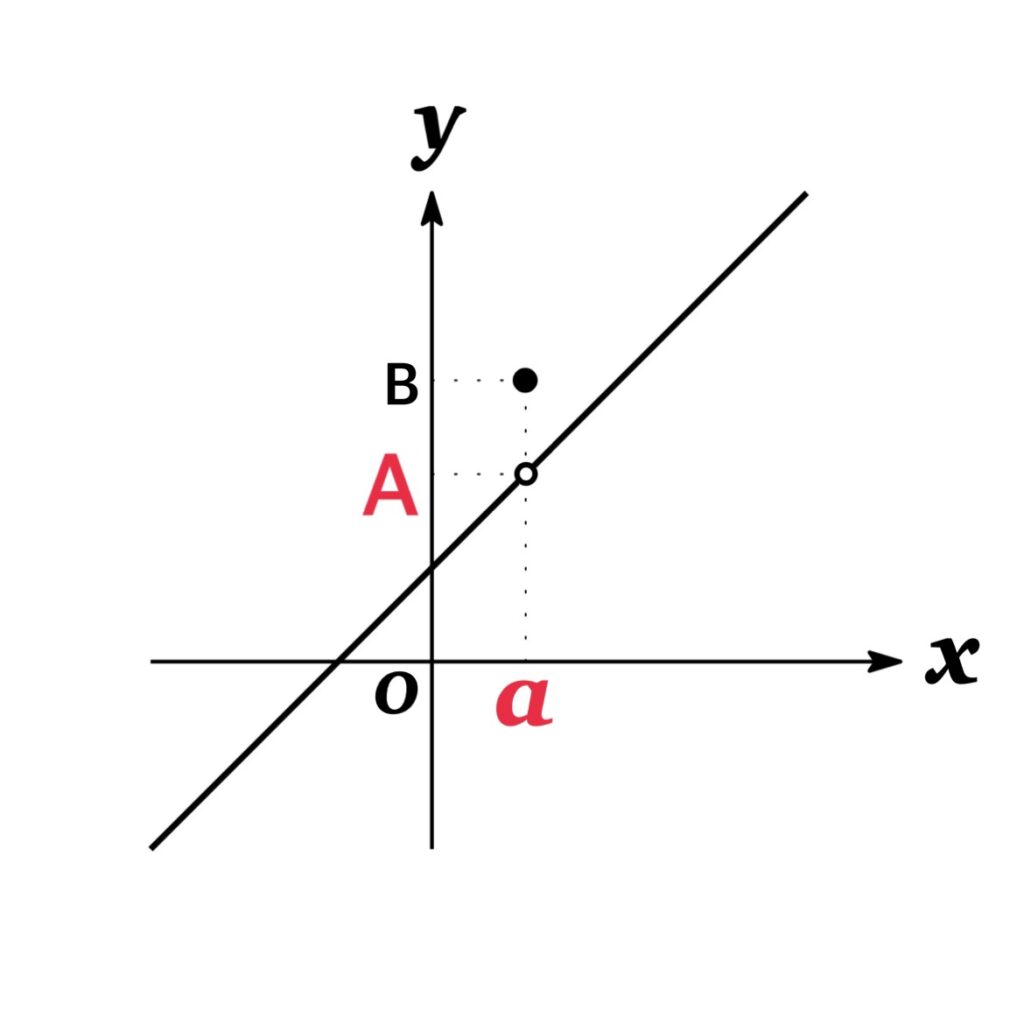
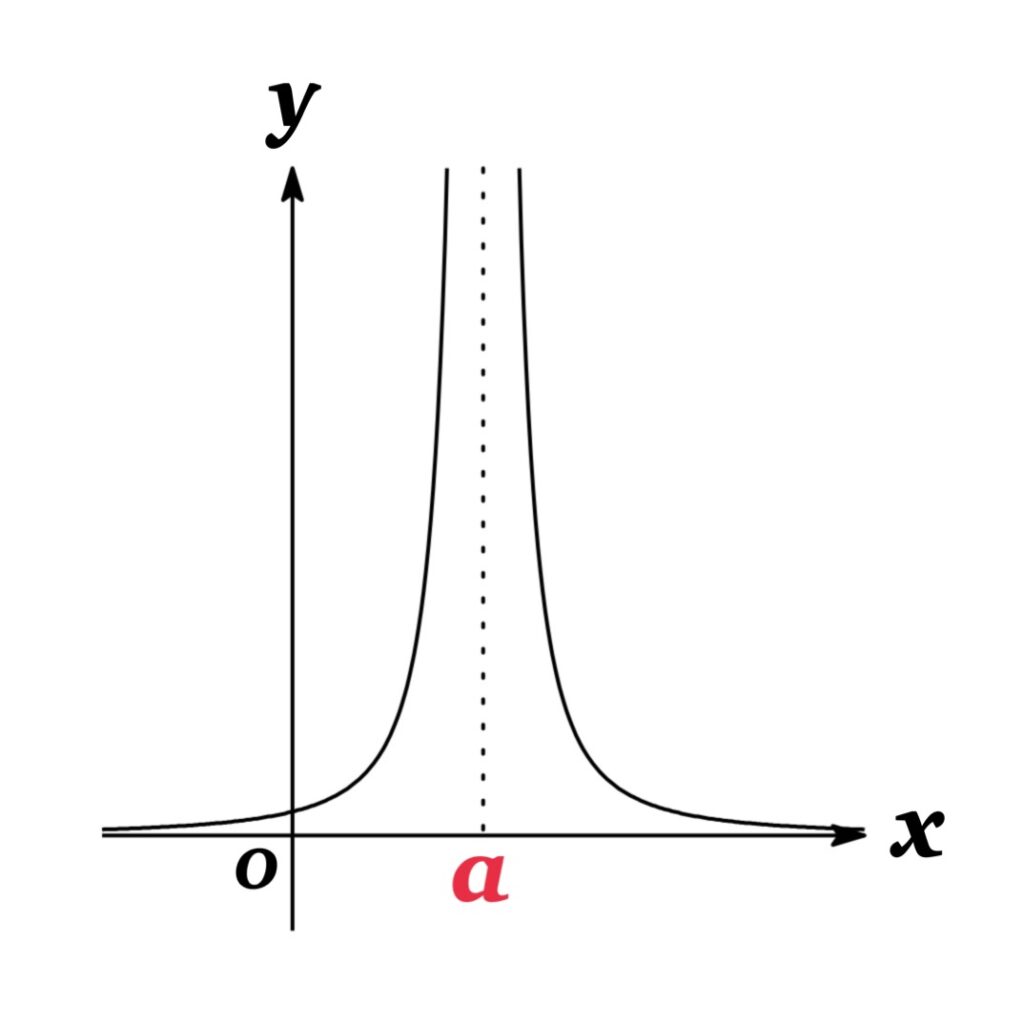
極限値 $\lim_{x\rightarrow a}f(x)$ が存在しない例:
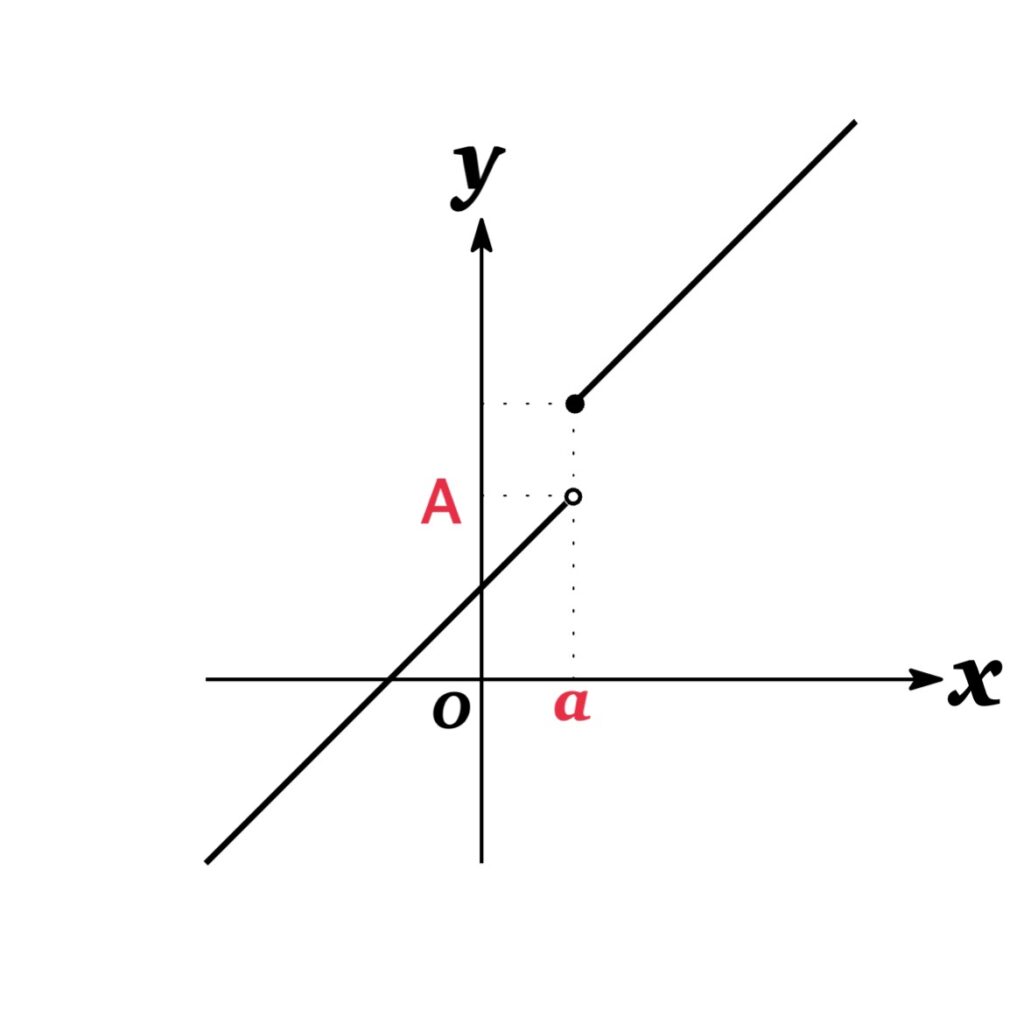
Contents
極限値が存在する場合
$\lim_{x\rightarrow 1}\frac{x^{2}-1}{x-1}=2$
$f(1)=\frac{1^{2}-1}{1-1}=\frac{0}{0}$ と不定形になっているので約分で式変形を行う.
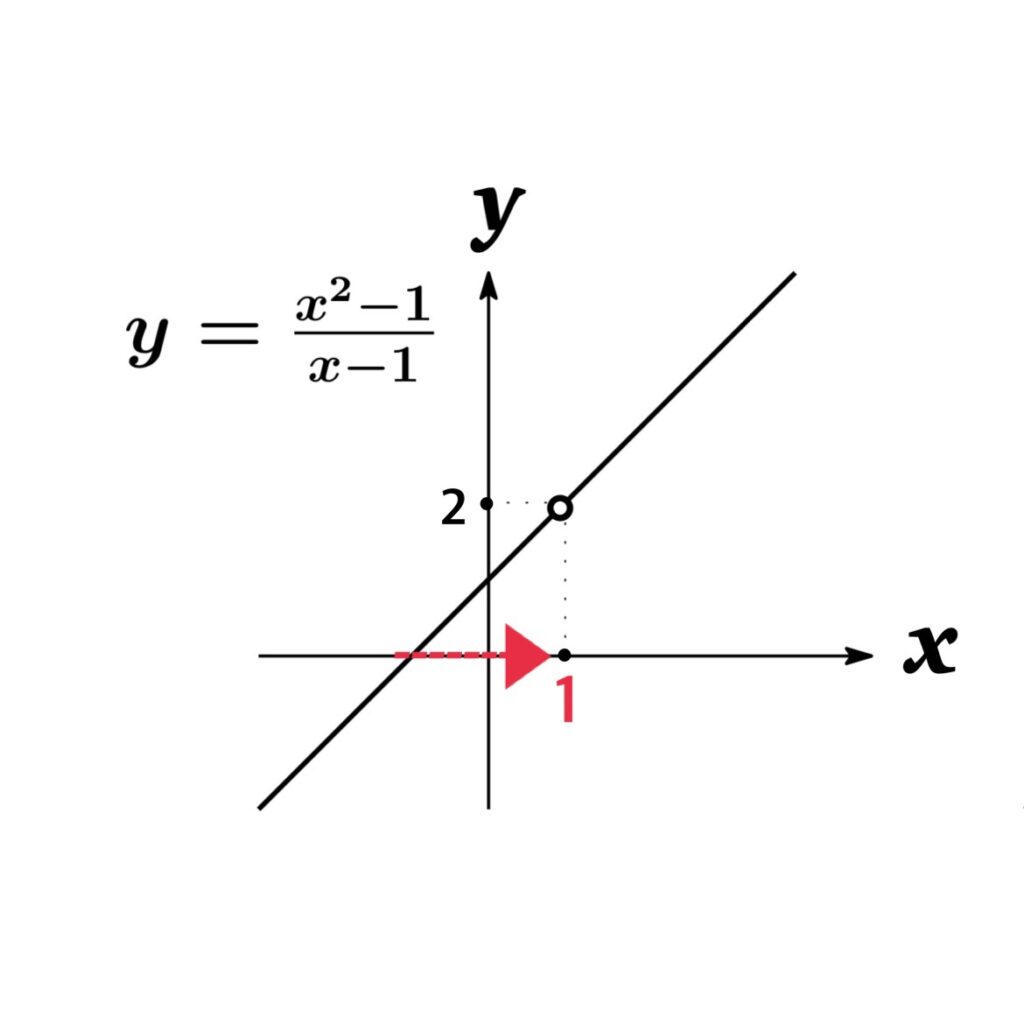
- 左側極限:$\lim_{x\rightarrow 1-0}\frac{x^{2}-1}{x-1}=\lim_{x\rightarrow 1-0}\frac{(x+1)(x-1)}{x-1}=\lim_{x\rightarrow 1-0}\ x+1=2$
- 右側極限:$\lim_{x\rightarrow 1+0}\frac{x^{2}-1}{x-1}=\lim_{x\rightarrow 1+0}\frac{(x+1)(x-1)}{x-1}=\lim_{x\rightarrow 1-0}\ x+1=2$
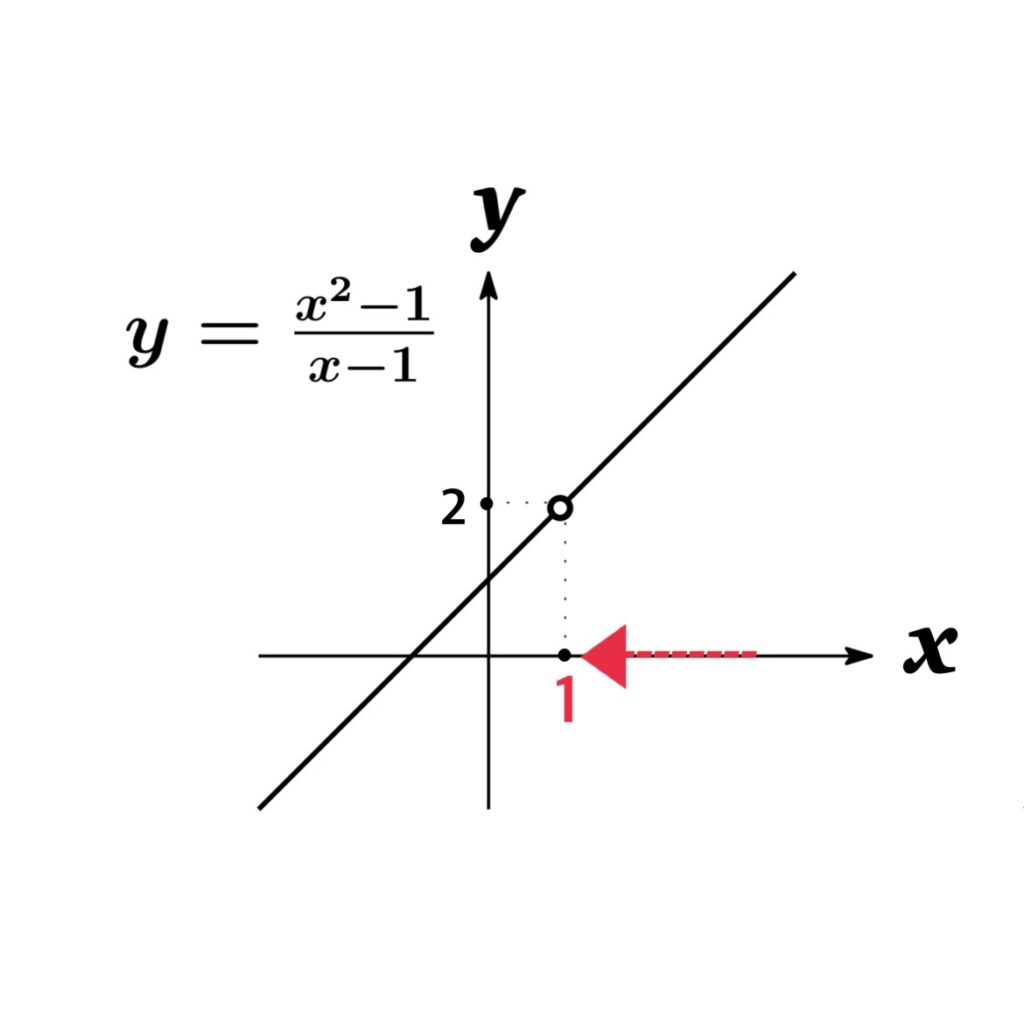
$\displaystyle\lim_{x\rightarrow -0} \frac{x^{2}-1}{x-1}=\displaystyle\lim_{x\rightarrow +0} \frac{x^{2}-1}{x-1}$より
$x=1$ における 極限値は $\lim_{x\rightarrow 1}\frac{x^{2}-1}{x-1}=2$ となる.
ただし $x=1$ において $f(x)=\frac{x-1}{x^{2}-1}$ は定義されていないことに注意する.
極限値が存在するとき, $f(x)$ は $x\rightarrow a $ で $A$ に収束するという.
極限値が存在しない場合
右側極限 $\not=$ 左側極限の場合
例題 :$\displaystyle\lim_{x\rightarrow -1} [x]$ は存在しない.
ただし $[x]$ はガウス記号と呼ばれ, $[x]$ は $x$ 以下の最大の整数を表す.
- 左側極限:$\displaystyle\lim_{x\rightarrow -1-0} [x]=-2$
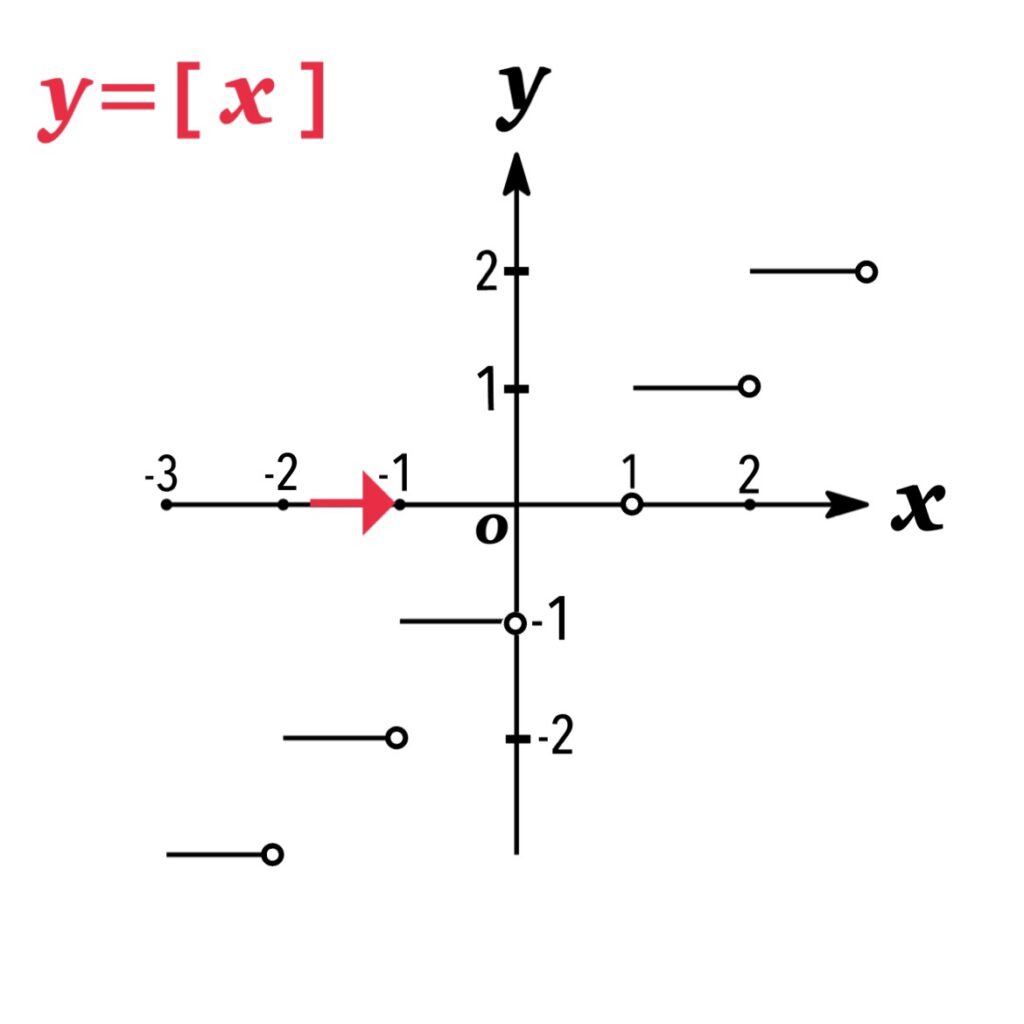
- 右側極限:$\displaystyle\lim_{x\rightarrow -1+0} [x]=-1$
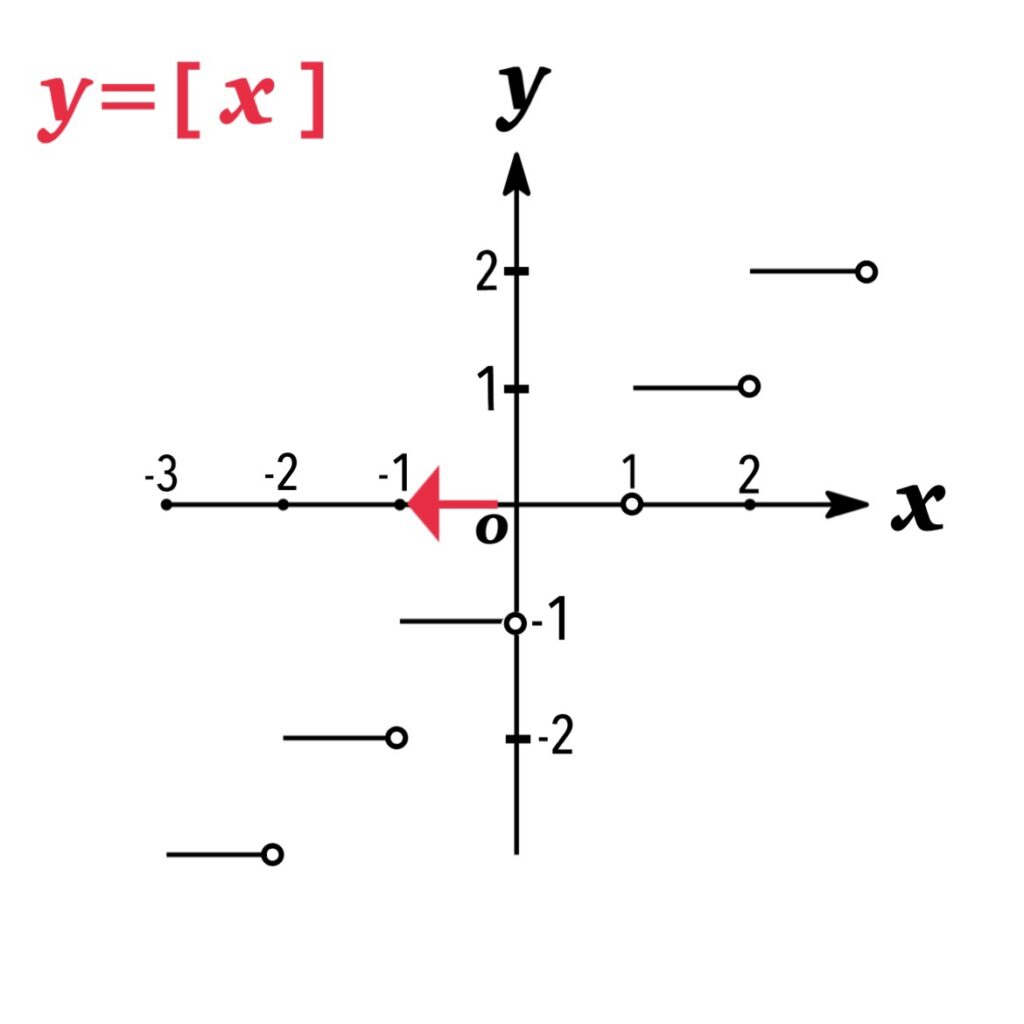
$\displaystyle\lim_{x\rightarrow-1 -0} [x]\not=\displaystyle\lim_{x\rightarrow -1+0} [x]$.
よって極限値は存在しない.
極限値が発散する場合
例題:$\lim_{x\rightarrow a}\frac{1}{x^{2}}=\infty$
左側極限:$\displaystyle\lim_{x\rightarrow -0} \frac{1}{x}=\infty$
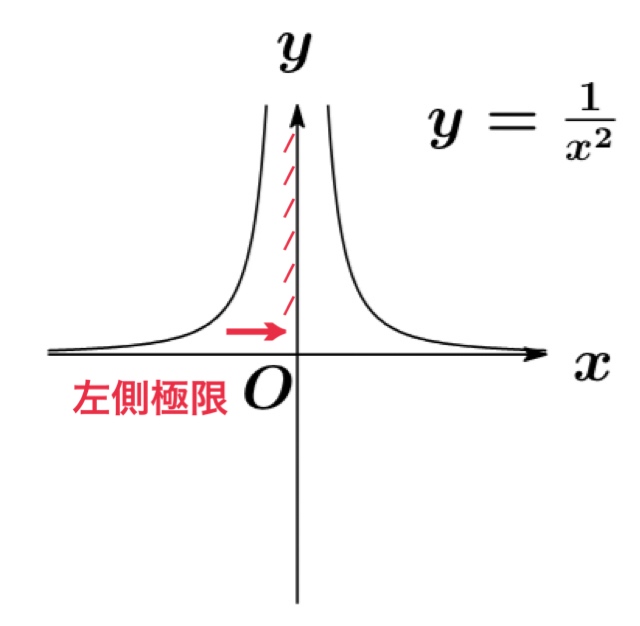
右側極限:$\displaystyle\lim_{x\rightarrow +0} \frac{1}{x}=\infty$
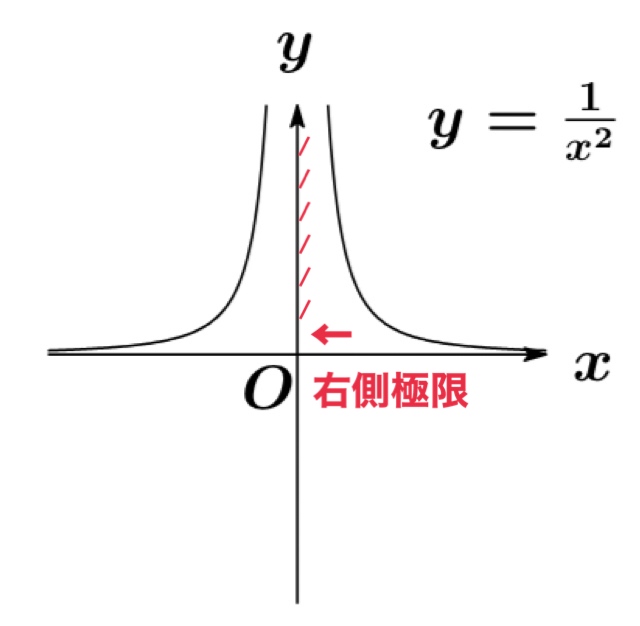
$\displaystyle\lim_{x\rightarrow -0} \frac{1}{x^{2}}=\displaystyle\lim_{x\rightarrow +0} \frac{1}{x^{2}}$ より
$\displaystyle\lim_{x\rightarrow 0} \frac{1}{x^{2}}=\infty $
ただし $\infty$ や $-\infty$ に発散する場合, 極限値とは言わないので注意する.
$x\rightarrow a $ で $f(x)$ が限りなく大きく (または小さく) なるとき , $\lim_{x\rightarrow a}f(x)=\infty$ (または $-\infty$) で表し, $f(x)$ は $x\rightarrow a $ で $\infty$ (または $-\infty$) に発散するという.
振動する場合
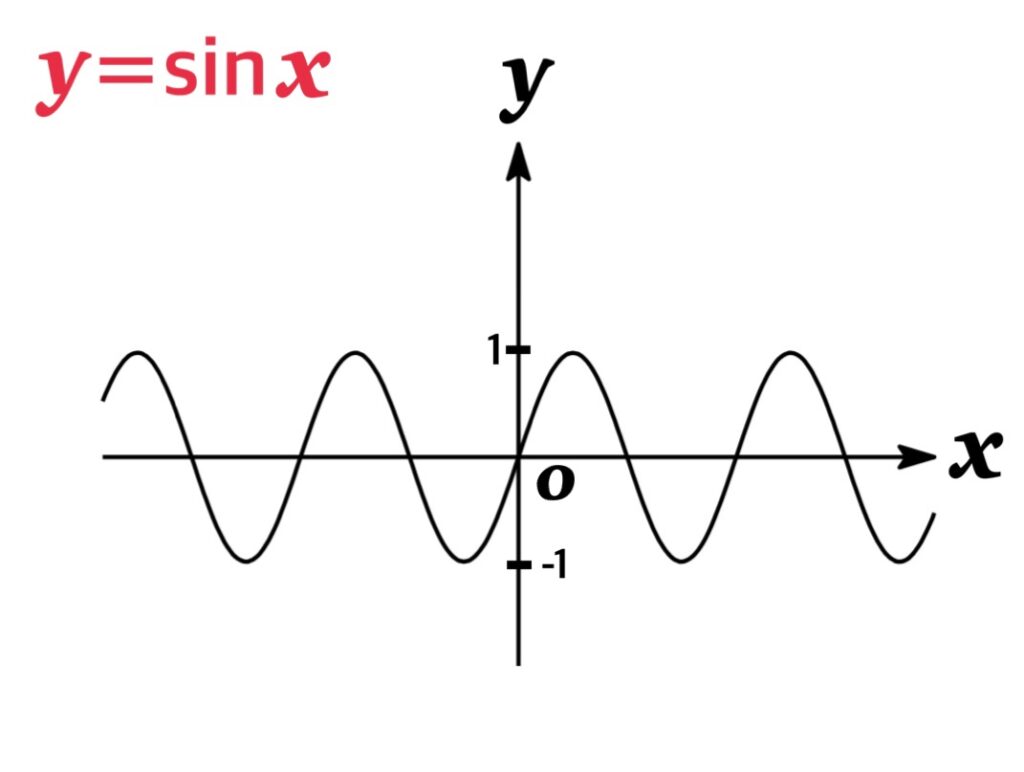
$\lim_{x\rightarrow \infty} \sin x$ は 振動する.
$y=\sin x$ は $x\rightarrow \infty $ のとき, $-1\leq y\leq 1$ で振動し, 値が定まらない.
よって極限値は存在しない.
なお, 振動する場合も発散するに含まれる.
不定形の極限値
$\frac{0}{0},\ \frac{\infty}{\infty}, \infty-\infty,\ 0\times \infty$ となるような極限を不定形と呼ぶ.
$\frac{0}{0}$ の不定形
$\frac{0}{0}$ の不定形
(1)分数式の場合は約分する.
(2)無理式の場合は有理化する.
分数式の場合:$\lim_{x\rightarrow 1}\frac{x^{2}-1}{x-1}=\lim_{x\rightarrow 1} \frac{(x+1)(x-1)}{x-1}=\lim_{x\rightarrow 1} (x+1) = 2$
無理式の場合:
$\begin{eqnarray*}\lim_{x\rightarrow 0}\frac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}&=&\lim_{x\rightarrow 0}\frac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}\times \frac{(\sqrt[3]{1+x})^{2}+(\sqrt[3]{1+x})(\sqrt[3]{1-x})+(\sqrt[3]{1-x})^{2}}{(\sqrt[3]{1+x})^{2}+(\sqrt[3]{1+x})(\sqrt[3]{1-x})+(\sqrt[3]{1-x})^{2}}\\&=&\lim_{x\rightarrow 0}\frac{(1+x)-(1-x)}{x\{\sqrt[3]{(1+x)^{2}}+\sqrt[3]{(1+x)}\sqrt[3]{(1-x)}+\sqrt[3]{(1-x)^{2}}\}}\\&=&\lim_{x\rightarrow 0}\frac{2}{\{\sqrt[3]{(1+x)^{2}}+\sqrt[3]{(1+x)}\sqrt[3]{(1-x)}+\sqrt[3]{(1-x)^{2}}\}}\\&=&\frac{2}{1+1+1}=\frac{2}{3}\end{eqnarray*}$
$\frac{\infty}{\infty}$ の不定形
$\frac{\infty}{\infty}$ の不定形
分数式において、分母の最高次の項で分母・分子を割る.
分数式の場合:$\lim_{x\rightarrow \infty} \frac{2x^{2}-3}{x^{2}-3x+5}=\lim_{x\rightarrow \infty} \frac{2-\frac{3}{x^{2}}}{1-\frac{3}{x}+\frac{5}{x^{2}}}=2$
$\infty-\infty$ の不定形
$\infty-\infty$ の不定形
(1)整式の場合, 最高次の項をくくりだす
(2)無理式の場合, 有理化をする
整式の場合:最高次の $x^{3}$ でくくりだす:
$\lim_{x\rightarrow \infty} (2x^{3}-3x^{2}+4)=\lim_{x\rightarrow \infty} x^{3}(2-\frac{3}{x}+\frac{4}{x^{3}})=-\infty$
無理式の場合:分子の有理化を行う:
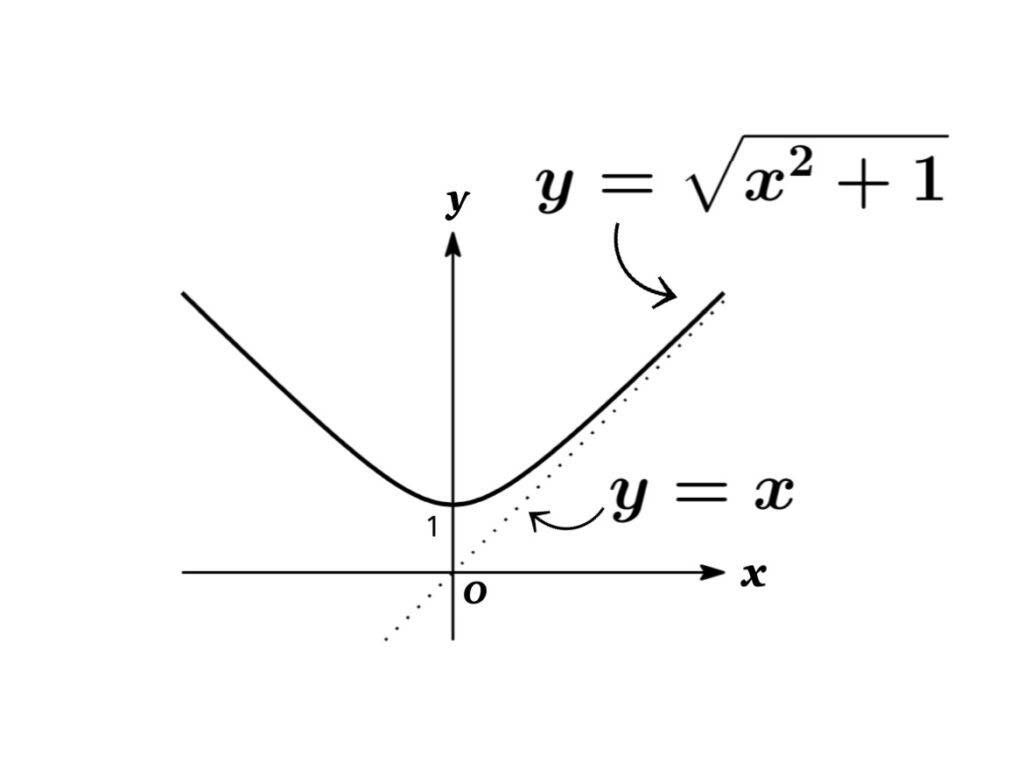
$\begin{eqnarray*}\lim_{x\rightarrow \infty}(\sqrt{x^{2}+1}-x)&=&\lim_{x\rightarrow \infty} \frac{(\sqrt{x^{2}+1}-x)(\sqrt{x^{2}+1}+x)}{(\sqrt{x^{2}+1}+x)}\\&=&\lim_{x\rightarrow \infty} \frac{(x^{2}+1)-x^{2}}{\sqrt{x^{2}+1}+x}\\&=&\lim_{x\rightarrow \infty} \frac{1}{\sqrt{x^{2}+1}+x}\\&=&\frac{1}{\infty}=0\end{eqnarray*}$
ちなみに・・・この例から, 関数 $y=\sqrt{x^{2}+1}$ のグラフは $y=x$ を漸近線にもつことがわかる.
不定形の極限の場合, 式変形によって極限値を求めるほかに、ロピタルの定理を用いることも可能である.