自然数 $n$ に対して, $(x+y)^{n}$ の展開式は二項定理により 次で与えられる.
$$(x+y)^{n}=\displaystyle\sum_{k=0}^{n} {}_{n}\mathrm{C}_{k}x^{n-k}y^{k}$$
この定理は $(x+y),\ (x+y)^{2},\ (x+y)^{3},\cdots$ の一般化であり, 二項定理は $(x+y)^{n}$ を展開したとき $x^{n-k}y^{k}$ の係数は ${}_{n}\mathrm{C}_{k}$ となることを意味している. 例えば, $(x+y)^{3}$ の展開式における $x^{2}y^{1}$ の係数は ${}_{3}\mathrm{C}_{1}=3$ で与えられる.
| 展開式 | ${}_{n}\mathrm{C}_{k}$ 記法 | |
| $(x+y)^{1}=x+y$ | $(x+y)^{1}={}_{1}\mathrm{C}_{0}x^{1}y^{0}+{}_{1}\mathrm{C}_{1}x^{0}y^{1}$ | |
| $(x+y)^{2}=x^{2}y+2xy+y^{2}$ | $(x+y)^{2}={}_{2}\mathrm{C}_{0}x^{2}y^{0}+{}_{2}\mathrm{C}_{1}x^{1}y^{1}+{}_{2}\mathrm{C}_{2}x^{0}y^{2}$ | |
| $(x+y)^{3}=x^{3}+3x^{2}y+3xy^{2}+y^{3}$ | $(x+y)^{3}={}_{3}\mathrm{C}_{0}x^{3}y^{0}+{}_{3}\mathrm{C}_{1}x^{2}y^{1}+{}_{3}\mathrm{C}_{2}x^{1}y^{2}+{}_{3}\mathrm{C}_{3}x^{0}y^{3}$ |
$(x+y)^{n}$ の展開式における $x^{k}y^{n-k}$ の係数 ${}_{n}\mathrm{C}_{k}$ は二項係数と呼ばれ, $0\leq k\leq n$ に対して
$${}_{n}\mathrm{C}_{k}=\frac{n\cdot (n-1)\cdots (n-k+1)}{k!}=\frac{n!}{k!(n-k)!}$$
を満たす. ( ${}_{n} {C}_{k}$ は $n$ 個から $k$ 個を選ぶ組合せの数を表している. )ただし
$${}_{n}\mathrm{C}_{0}=1, \ \ x^{0}=y^{0}=1$$
とする. また大学では ${}_{n}\mathrm{C}_{k}=\left(\begin{array}{c}n\\k\end{array}\right)$ の表記を用いることもある.
二項係数の性質
| ${}_{n}\mathrm{C}_{k}={}_{n}\mathrm{C}_{n-k}$ | 証明 |
| ${}_{n-1}\mathrm{C}_{k-1}+{}_{n-1}\mathrm{C}_{k}={}_{n}\mathrm{C}_{k}$ | 証明 |
| $k\times {}_{n}\mathrm{C}_{k}=n\times {}_{n-1}\mathrm{C}_{k-1}$ | 証明 |
二項係数の成り立ち
$(x+y)^{n}$ の展開式における $x^{k}y^{n-k}$ の係数は
$$(x+y)(x+y)\cdots (x+y)$$
の $n$ 個の積から $x$ を $(n-k)$ 個、$y$ を $k$ 個取り出して $x^{n-k}y^{k}$をつくる組合せの数になることから, ${}_{n}\mathrm{C}_{k}$ となる.
パスカルの三角形
${}_{n}\mathrm{C}_{k}$ には
$${}_{n}\mathrm{C}_{k}={}_{n-1}\mathrm{C}_{k}+{}_{n-1}\mathrm{C}_{k-1}$$
という関係式が成立することから、パスカルの三角形は二項係数を並べたものとみなすことができる.
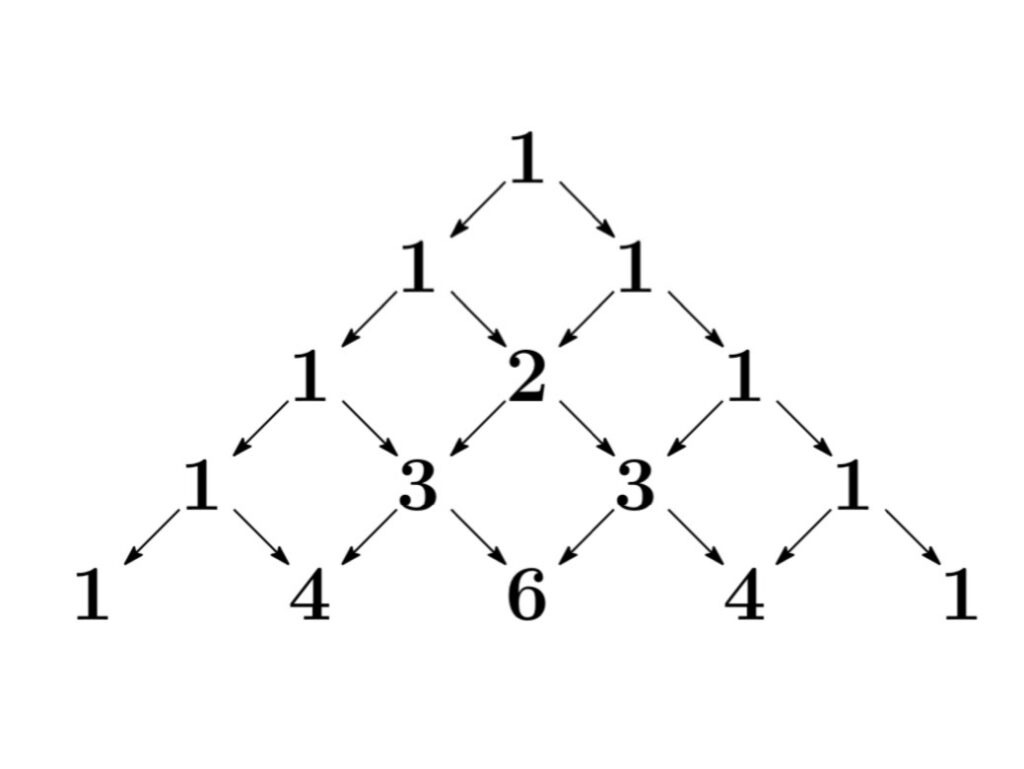
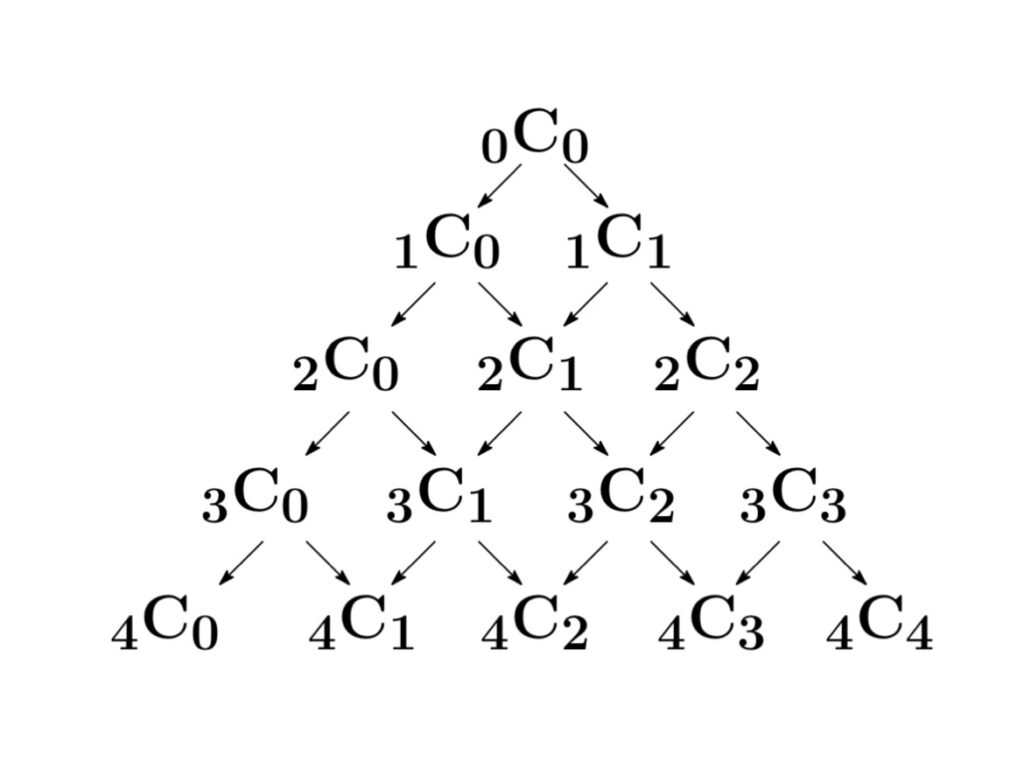
負の二項係数
$-n$ を負の整数とするとき $$(x+y)^{-n}=\displaystyle\sum_{k=0}^{\infty}{}_{-n}\mathrm{C}_{k} x^{-n-k}y^{k}=\displaystyle\sum_{k=0}^{\infty} (-1)^{k}{}_{n+k-1}\mathrm{C}_{k} x^{k}y^{-n-k}$$
これまで二項定理では 正の整数 $n$ に対して定義されていたが、負の二項定理では $n$ が整数全体に拡張されたものである.
ここで${}_{-n}\mathrm{C}_{k}$ は
$${}_{-n}\mathrm{C}_{k}=\frac{-n\cdot (-n-1)\cdots (-n-k+1)}{k!}$$ で定義される. また $$(-n)\cdot (-n-1)\cdots (-n-k+1)=(-1)^{k}(n+k-1)\cdots(n+1)\cdot (n)$$より $${}_{-n}\mathrm{C}_{k}=(-1)^{k}{}_{n+k-1}\mathrm{C}_{k}$$の関係式を満たす.
Example
$\frac{1}{(1+x)^{2}}$ を級数展開せよ.
Solution : ${}_{-2} C_{k}=(-1)^{k} {}_{2+k-1}C_{k}=(-1)^{k} (k+1)$ より
\begin{eqnarray*}\frac{1}{(1+x)^{2}}&=&(1+x)^{-2}=\displaystyle\sum_{k=0}^{\infty}{}_{-2} C_{k} x^{k}\\&=&\displaystyle\sum_{k=0}^{\infty}(-1)^{k}(k+1) x^{k}\\&=&1-2x+3x^{2}-4x^{3}+5x^{4}-6x^{5}+\cdots \end{eqnarray*}