関数 \(f(x)\) が \(x=a\) で連続であるとは, 直観的には \(x=a\) でグラフがつながっていることであるが正確な定義は以下のようになる.
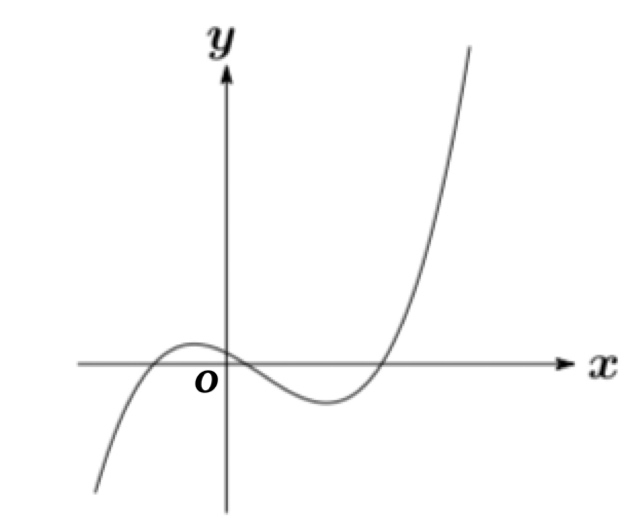
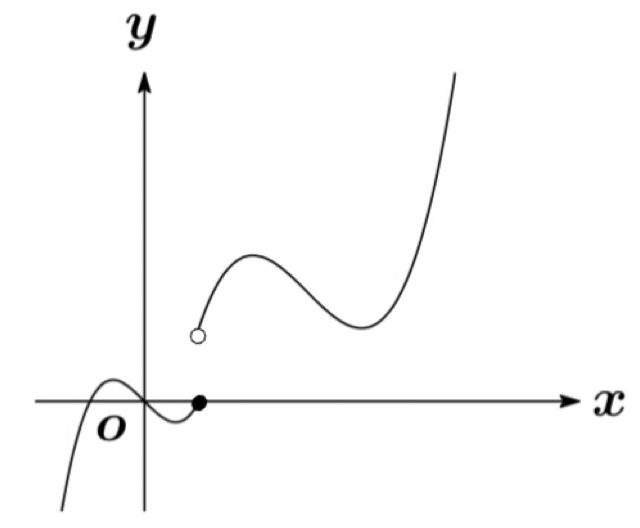
関数 $f(x)$ が $$\displaystyle\lim_{x\rightarrow a+0} f(x) =f(a) \ \text{かつ} \displaystyle\lim_{x\rightarrow a-0} f(x)=f(a)$$
が成り立つとき, $f(x)$ は $x=a$で連続であるという.
すなわち x=a における\(f(x)\)の右側極限値・左側極限値が存在して $$\text{右側極限値:} \displaystyle\lim_{x\rightarrow a+0} f(x) =f(a) $$
$$\text{左側極限値:}\displaystyle\lim_{x\rightarrow a-0} f(x)=f(a)$$その値が等しいとき
$$\displaystyle\lim_{x\rightarrow a+0} f(x)=\displaystyle\lim_{x\rightarrow a-0} f(x)$$ $f(x)$ は$x=a$で連続であるという.
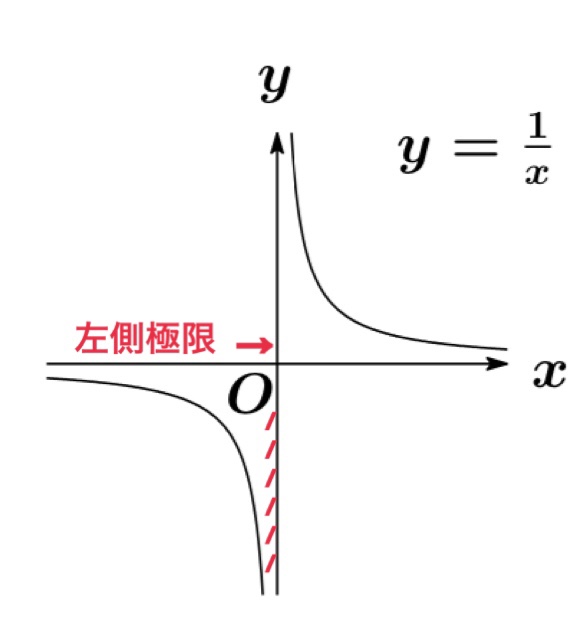
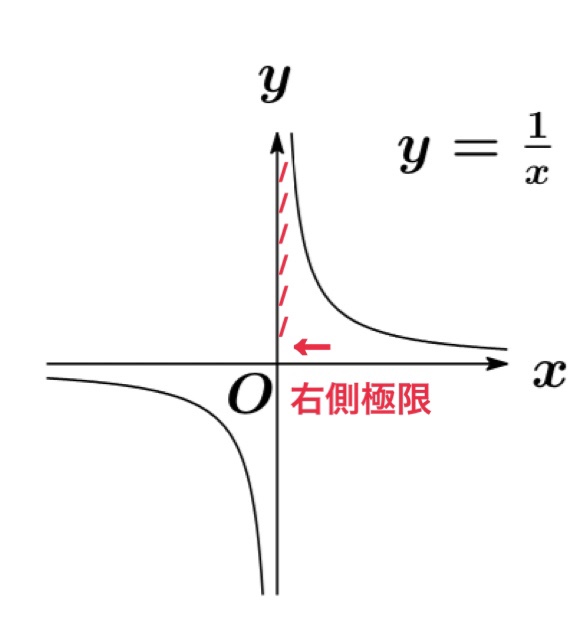
例
$x=0$ における $y=|x|$ の連続性について
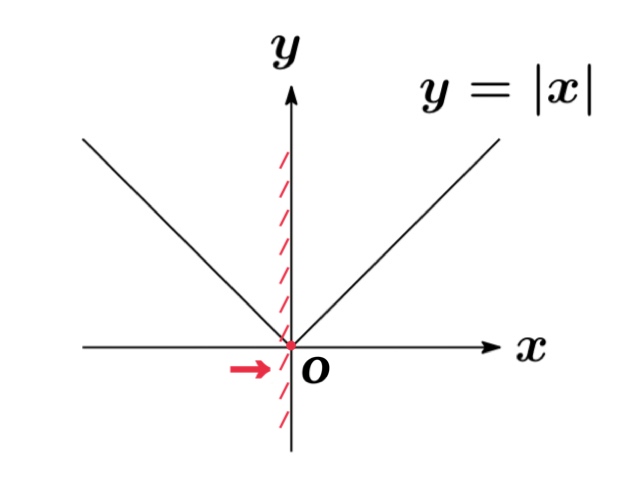
左側極限値:$\displaystyle\lim_{x\rightarrow -0} |x|=0$
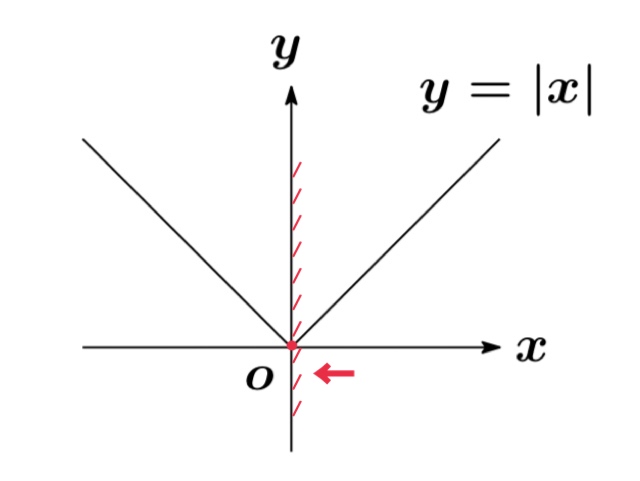
右側極限値:$\displaystyle\lim_{x\rightarrow +0} |x|=0$
以上より 「左側極限値・右側極限値が存在し」 かつ 「その値が等しい」ことから $x=0$ で $y=|x|$ は連続であることが示される.
$f(x)=\begin{cases}x\sin \frac{1}{x}& (x\not =0)\\0 &(x=0)\end{cases}$ の連続性について
$x\not=0$ のとき $f(x)$ が連続であることは明らか.
$x=0$ のとき
$0\leq|\sin \frac{1}{x}|\leq 1$ より各辺に $|x|$ をかけると
$$0\leq|x\sin \frac{1}{x}|\leq |x|$$
となる. このとき $\displaystyle\lim_{x\rightarrow 0}|x|=0$ より はさみうちの原理を用いると
$$\displaystyle\lim_{x\rightarrow 0}|x\sin \frac{1}{x}|=0$$
となる. よって $\displaystyle\lim_{x\rightarrow a} |f(x)|=0$ ならば$\displaystyle\lim_{x\rightarrow a} f(x)=0$ であるので(極限値参照)
$\displaystyle\lim_{x\rightarrow 0}x\sin \frac{1}{x}=0$ が成り立ち$x=0$ のときも $f(x)$ は連続である.
連続関数の性質
関数 $f(x), g(x)$ が $x=a$で連続であるとき
$$cf(x)(c\text{は定数}),\ f(x)\pm g(x),\ f(x)g(x),\ \frac{f(x)}{g(x)}(g(a)\not= 0)$$
も $x=a$で連続である.
$x$ の多項式, $\sin x,\ \cos x,\ \mathrm{e}^{x}$ などはすべての $x$ で連続であり, $\tan x$ は定義域 $x\not= \frac{\pi}{2}+n\pi( n$ は整数) , $\log x$ は定義域 $x>0$ でそれぞれ連続である.