Suppose that $x$ and $y$ are both given as functions of a variable $t$ by the equations
$$x=f(t),\ \ \ y=g(t)$$
and this is called parametric equations. Also, $t$ is called a parameter. Each value of $t$ determines a point $(x,y)=\left(f(t),\ g(t)\right)$.
Example
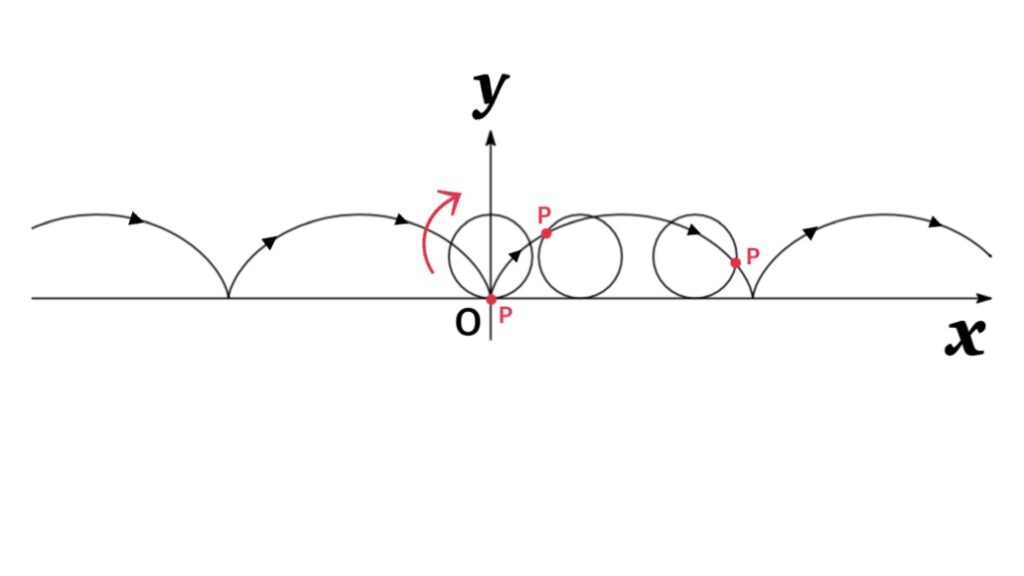
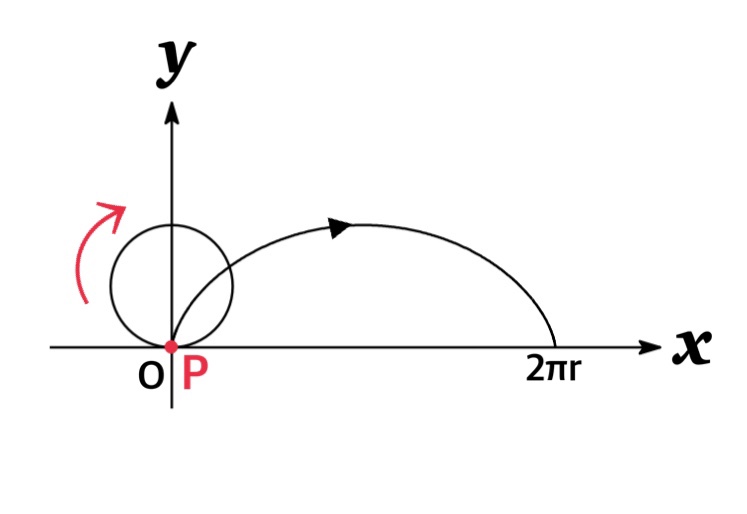
The curve traced out by a point P on the circumference of a circle as the circle rolls along a straight line is called a cycloid .
If the circle has radius $r$ and rolls along the $x$-axis and if one position of $P$ is the origin, the parametric equations for the cycloid is given by
$$\begin{eqnarray*}x&=&r(t-\sin t)\\y&=&r(1-\cos t)\end{eqnarray*}$$
where $t$ is a parameter which is the angle of rotation of the circle. (That is, $t=0$ when $P$ is at the origin.)
Derivatives
In the case of differentiation of parametric equations \(x=f(t)\) and \(y=g(t)\), we have
$$\frac{dy}{dx}=\frac{\ \ \ \frac{dy}{dt}\ \ \ }{\ \ \ \frac{dx}{dt}\ \ \ }=\frac{g'(t)}{f'(t)}\ \ \ \ \ \text{if}\ \ \ \frac{dx}{dt}\not= 0$$
Notice that the curve, defined by parametric equations \(x=f(t)\) and \(y=g(t)\), has a horizontal tangent when \(\frac{dy}{dt}=0\) and has a vertical tangent when \(\frac{dx}{dt}=0\).
Example : Find the tangent to the cycloid $x=r(t-\sin t),\ \ \ y=r(1-\cos t)$ at the point $t=\frac{\pi}{3}$.
Solution : The slope of the tangent line is
$$\frac{dy}{dx}=\frac{\ \ \ \frac{dy}{dt}\ \ \ }{\ \ \ \frac{dx}{dt}\ \ \ }=\frac{r\sin t}{r(1-\cos t)}=\frac{\sin t}{1-\cos t}$$
When $t=\frac{\pi}{3}$, we have $(x,\ y)=\left(r(\frac{\pi}{3}-\frac{\sqrt{3}}{2}),\ \frac{r}{2}\right)$ and
$$\frac{dy}{dx}=\frac{\sin(\frac{\pi}{3}) }{1-\cos(\frac{\pi}{3})}=\sqrt{3}$$
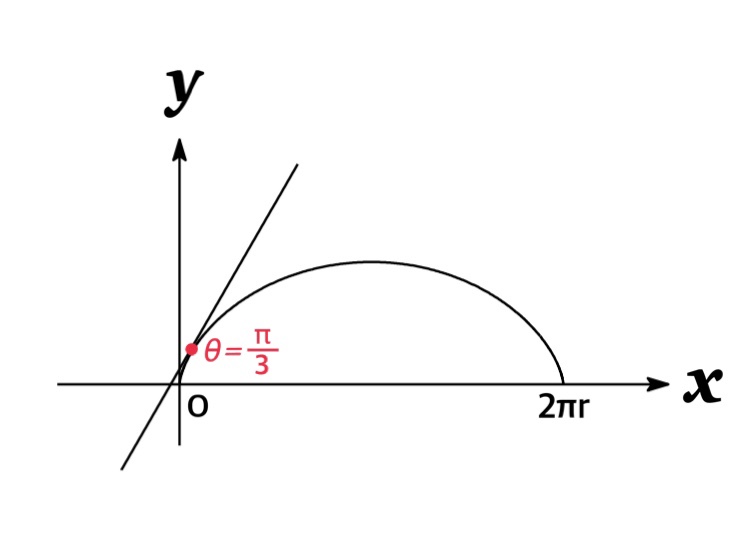
Therefore, the slope of the tangent is $\sqrt{3}$ and the tangent line is given by
$$y-\frac{r}{2}=\sqrt{3}\left(x-r(\frac{\pi}{3}-\frac{\sqrt{3}}{2})\right)$$
Thus we get
$$y=\sqrt{3}x+r(2-\frac{\pi}{\sqrt{3}})$$
Areas
If a curve described by parametric equations $x=f(t),\ y=g(t)$ and is traversed once as $t$ increase from $\ \alpha$ to $\beta$. Then the area under a curve from $\alpha$ to $\beta$, bounded the vertical line $x=\alpha$ and $x=\beta$, and $x$-axis is given by
$$ A=\int g(t)f'(t)\ dt$$
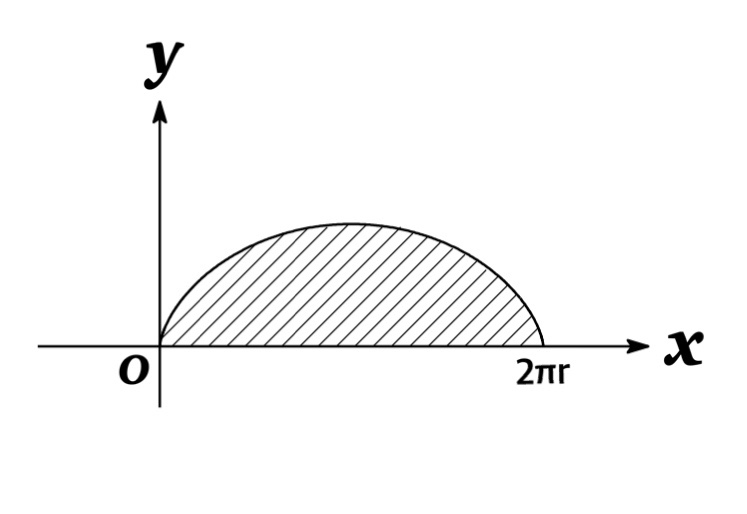
Example : Find the area under one arch of the cycloid $x=r(t-\sin t),\ \ \ y=r(1-\cos t)$.
Solution : One arch of the cycloid is described by the parameter interval $0\leq t\leq 2\pi$. Since we have
$$y=g(t)=r(1-\cos t),\ \ \ \frac{dx}{dt}=r(1-\cos t)$$
we have
$$\begin{eqnarray*}A&=&\int_{0}^{2\pi} r(1-\cos t)\cdot r(1-\cos t)\ dt=r ^{2}\int_{0}^{2\pi} (1-2\cos t+\cos^{2} t)\ dt\\&=&r^{2} \int_{0}^{2\pi} (1-2\cos t+\frac{1}{2}(1+\cos 2t))\ dt\ \ \ (\text{∵ half-angle formula})\\&=&r^{2}[\frac{3}{2}t-2\sin t+\frac{1}{4}\sin 2t ]_{0}^{2\pi}\\&=&3\pi r^{2}\end{eqnarray*}$$
Notice that to evaluate the interval we use the identity (half- angle formula ) :$\cos^{2} t=\frac{1}{2}(1+\cos 2t)$.
Arc Length
If a curve described by parametric equations $x=f(t),\ y=g(t),\ \alpha\leq t\leq \beta$, the length of the curve is given by
$$ L=\int_{\alpha}^{\beta} \sqrt{\{f'(t)\}^{2}+\{g'(t)\}^{2}}\ dt=\int_{\alpha}^{\beta} \sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\ dt$$
Example : Find the length of one arch of the cycloid $x=r(t-\sin t),\ \ \ y=r(1-\cos t)$.
Solution : One arch of the cycloid is described by the parameter interval $0\leq t\leq 2\pi$. Then
$$\frac{dx}{dt}=r(1-\cos t),\ \ \ \frac{dy}{dt}=r\sin t$$
Therefore, we have
$$L=\int_{0}^{2\pi} \sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\ dt=\int_{0}^{2\pi} \sqrt{r^{2}(1-\cos t)^{2}+r^{2}\sin^{2} t}\ dt=r \int_{0}^{2\pi} \sqrt{2(1-\cos t)}\ dt$$
Now, to evaluate the interval we use the identity (half- angle formula ) :$\sin^{2} t=\frac{1}{2}(1-\cos 2t)$ which gives $1-\cos t=2\sin^{2} \frac{t}{2}$.
Since $0\leq t\leq 2\pi$, we have $0\leq \frac{t}{2}\leq \pi$ and so $\sin \frac{t}{2} \geq 0$. Therefore, we have
$$\sqrt{2(1-\cos t)}=\sqrt{4\sin^{2} \frac{t}{2}}=2|\sin \frac{t}{2}|=2\sin \frac{t}{2}$$
and we obtain
$$L=2r \int_{0}^{2\pi} \sin \frac{t}{2}\ dt=2r[-2 \cos \frac{t}{2}]_{0}^{2\pi}=2r[2+2]=8r$$
Surface Area
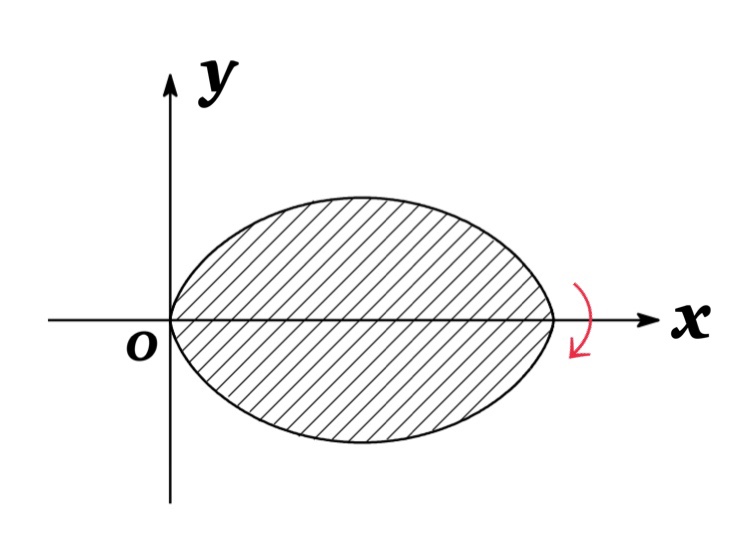
If a curve described by parametric equations $x=f(t),\ y=g(t),\ \alpha\leq t\leq \beta$, is rotated about the $x$-axis, then the area of the resulting surface is given by
$$ S=\int_{\alpha}^{\beta} 2\pi y\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\ dt$$
Example : Find the surface area of one arch of the cycloid $x=r(t-\sin t),\ \ \ y=r(1-\cos t)$ by rotating about $x$-axis.
Solution : One arch of the cycloid is described by the parameter interval $0\leq t\leq 2\pi$. Then from the formula, we get
$$\begin{eqnarray*}S&=&\int_{0}^{2\pi} 2\pi\ y\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\ dt\\&=&\int_{0}^{2\pi} 2\pi\ r(1-\cos t)\sqrt{r^{2}(1-\cos t)^{2}+r^{2}\sin^{2} t}\ dt\\&=&2\pi r^{2} \int_{0}^{2\pi} (1-\cos t)\sqrt{2(1-\cos t)}\ dt\end{eqnarray*}$$
Now, to evaluate the interval we use the identity (half- angle formula ) :$\sin^{2} t=\frac{1}{2}(1-\cos 2t)$ which gives $1-\cos t=2\sin^{2} \frac{t}{2}$.
Since $0\leq t\leq 2\pi$, we have $0\leq \frac{t}{2}\leq \pi$ and so $\sin \frac{t}{2} \geq 0$. Therefore, we have
$$(1-\cos t)\sqrt{2(1-\cos t)}=2\sin^{2} \frac{t}{2} \sqrt{4\sin^{2} \frac{t}{2}}=4\sin^{2} \frac{t}{2}|\sin \frac{t}{2}|=4\sin^{3} \frac{t}{2}$$
and we have
$$S=2\pi r^{2} \int_{0}^{2\pi} 4\sin^{3} \frac{t}{2}\ dt=8\pi r^{2} \int_{0}^{2\pi} \sin^{2} \frac{t}{2}\cdot \sin \frac{t}{2}\ dt=8\pi r^{2} \int_{0}^{2\pi} (1-\cos^{2} \frac{t}{2})\sin \frac{t}{2}\ dt$$
Here, if we let $\cos \frac{t}{2}=z$, we have $\frac{dz}{dt}=-\sin \frac{t}{2}\cdot \frac{1}{2}$ and $1\leq z\leq -1$.
Therefore, we obtain
$$8\pi r^{2} \int_{1}^{-1} (1-z^{2})(-2\ dz)=16\pi r^{2} \int_{-1}^{1} (1-z^{2})\ dz=16\pi r^{2}[z-\frac{z^{3}}{3}]_{-1}^{1}=\frac{64}{3}\pi r^{2}$$