Let \(\mathbf{a}=(a_{1},a_{2},a_{3})\) and \( \mathbf{b}=(b_{1},b_{2},b_{3})\). Then the cross product of \(\mathbf{a}\) and \(\mathbf{b}\) is the vector $$\mathbf{a}\times \mathbf{b}=(a_{2}b_{3}-a_{3}b_{2},\ a_{3}b_{1}-a_{1}b_{3},\ a_{1}b_{2}-a_{2}b_{1})$$
The cross product \(\mathbf{a}\times \mathbf{b}\) is defined only when the cross product \(\mathbf{a}\) and \(\mathbf{b}\) are 3-dimensional vectors.
Note that the cross product \(\mathbf{a}\times \mathbf{b}\) is a vector, unlike the dot product \(\mathbf{a}\cdot \mathbf{b}\).
Example : If \(\mathbf{a}=(1,2,3)\) and \(\mathbf{b}=(4,5,6)\), then
$$\begin{eqnarray*}\mathbf{a}\times \mathbf{b}&=&(1,2,3)\times (4,5,6)\\&=&(2\cdot 6-3\cdot 5,\ 3\cdot 4-1\cdot 6,\ 1\cdot 5-2\cdot 4)\\&=&(-3,6,-3)\end{eqnarray*}$$
Represent by the notation of determinants
To memorize the Definition of the cross product \(\mathbf{a}\times \mathbf{b}\) easier, we can rewrite by using the notation of determinants.
Now , let us rewrite the vectors with the standard basis \(\mathbf{i},\ \mathbf{j},\ \mathbf{k}\) as below:
$$\begin{eqnarray*}\mathbf{a}&=&(\ a_{1}, a_{2}, a_{3}\ )=a_{1}\ \mathbf{i}+a_{2}\ \mathbf{j}+a_{3}\ \mathbf{k}\\ \mathbf{b}&=&(\ b_{1}, b_{2}, b_{3}\ \ )=\ b_{1}\ \mathbf{i} +b_{2}\ \mathbf{j}\ +b_{3}\ \mathbf{k}\end{eqnarray*}$$
where \(\mathbf{i}=(1,0,0),\ \mathbf{j}=(0,1,0),\ \mathbf{k}=(0,0,1)\).
Then we see that the cross product \(\mathbf{a}\times \mathbf{b}\) is given by
$$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}&\ \mathbf{j}&\ \mathbf{k}\\a_{1}& a_{2}& a_{3}\\b_{1}& b_{2}& b_{3}\end{array}\right|=\left|\begin{array}{cc}a_{2}& a_{3}\\ b_{2}& b_{3}\end{array}\right|\mathbf{i}-\left|\begin{array}{cc}a_{1}& a_{3}\\b_{1}& b_{3}\end{array}\right|\mathbf{j}+\left|\begin{array}{cc}a_{1}& a_{2}\\ b_{1}& b_{2}\end{array}\right|\mathbf{k}$$
Example
If \(\mathbf{a}=(1,2,3)=\mathbf{i}+2\mathbf{j}+3\mathbf{k}\) and \(\mathbf{b}=(4,5,6)=4\mathbf{i}+5\mathbf{j}+6\mathbf{k}\), then
$$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}&\ \mathbf{j}&\ \mathbf{k}\\1& 2& 3\\4& 5& 6\end{array}\right|=\left|\begin{array}{cc}2& 3\\ 5& 6\end{array}\right|\mathbf{i}-\left|\begin{array}{cc}1& 3\\4& 6\end{array}\right|\mathbf{j}+\left|\begin{array}{cc}1& 2\\ 4& 5\end{array}\right|\mathbf{k}=-3\mathbf{i}+6\mathbf{j}-3\mathbf{k}$$
Properties
Let \(\mathbf{a},\ \mathbf{b} \) and \(\mathbf{c} \) be are vectors, and \(m \) be a scalar.
Then, the cross products of vectors have the following properties:
$$\begin{eqnarray*}&&\mathbf{a}\times \mathbf{b}=-\mathbf{b}\times \mathbf{a}\\
&&(m\mathbf{a})\times \mathbf{b}=m(\mathbf{a}\times \mathbf{b})=\mathbf{a}\times (m\mathbf{b})\\
&&\mathbf{a}\times (\mathbf{b}+ \mathbf{c})=\mathbf{a}\times \mathbf{b}+\mathbf{a}\times \mathbf{c}\\
&&\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})=(\mathbf{a}\times \mathbf{b})\cdot \mathbf{c}\\
&&\mathbf{a}\times (\mathbf{b}\times \mathbf{c})=(\mathbf{a}\cdot \mathbf{c})\mathbf{b}-(\mathbf{a}\cdot \mathbf{b})\mathbf{c}
\end{eqnarray*}$$
These properties can be proved by using the definition of a cross product, writing the vector components. For example, here is one of Properties:
$$\begin{eqnarray*}\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})&=&a_{1}(b_{2}c_{3}-b_{3}c_{2})+a_{2}(b_{3}c_{1}-b_{1}c_{3})+a_{3}(b_{1}c_{2}-b_{2}c_{1})\\&=&a_{1}b_{2}c_{3}-a_{1}b_{3}c_{2}+a_{2}b_{3}c_{1}-a_{2}b_{1}c_{3}+a_{3}b_{1}c_{2}-a_{3}b_{2}c_{1}\\&=&(a_{2}b_{3}-a_{3}b_{2})c_{1}+(a_{3}b_{1}-a_{1}b_{3})c_{2}+(a_{1}b_{2}-a_{2}b_{1})c_{3}\\&=&(\mathbf{a}\times \mathbf{b})\cdot \mathbf{c}\end{eqnarray*}$$
Especially, the product \(\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})\) is called the scalar triple product and have the significance geometric interpretation.
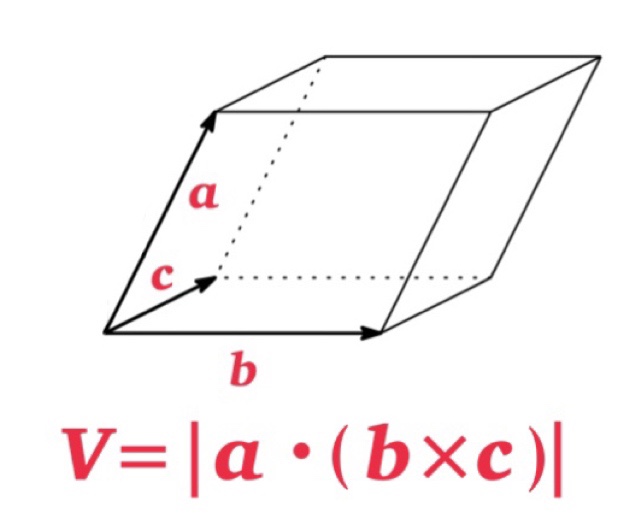
See Scalar triple products.