Let \(z=r(\cos \theta+i\sin\theta)\) and \(n\) be a positive integer. Then \(z\) has the \(n\) distinct \(n\)th roos
$$\omega_{k}=r^{\frac{1}{n}}\left[\cos \left(\frac{\theta+2k\pi}{n}\right)+i\sin \left(\frac{\theta+2k\pi}{n}\right)\right]\ (k=0,1,\cdots, n-1)$$
The solution of \( \omega^{n}=z\) is called the \(n\) th roots of a complex number \(z\).
All points, \(\omega_{0},\ \omega_{1},\ \cdots,\ \omega_{n-1}\), lie on the circle of radius \(r^{\frac{1}{n}}\), and are the vertices of a regular n-polygon.
Remark :\(\omega_{k}\) is represented by \(\omega_{k}=\omega_{0}z_{k}\) where \(z_{k}\) is the nth roots of 1.
Example
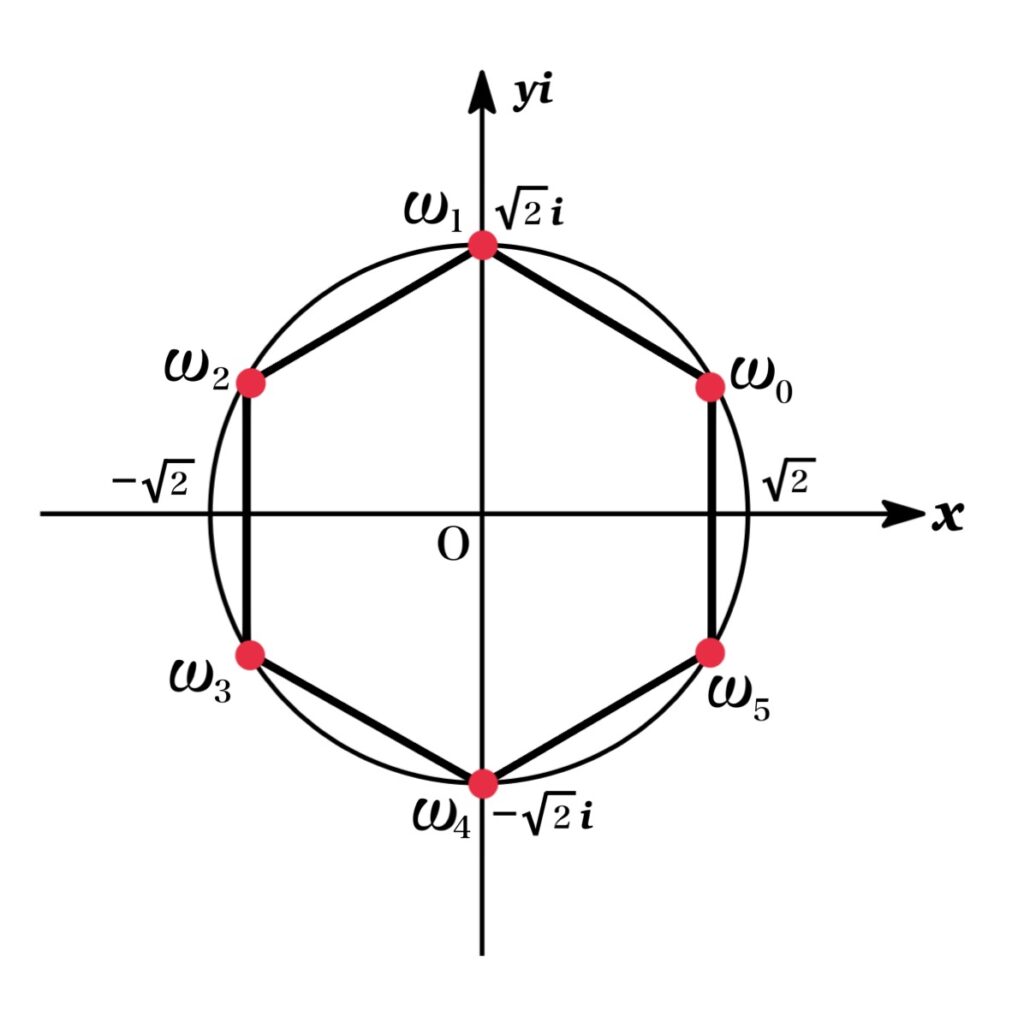
Find the solutions of \(\omega^{6}=8\).
We will find the sixth roots of \(z=8\), that is the solutions of \(\omega^{6}=8\).
In trigonometric form, we have \(z=8=8(\cos \pi+i\sin\pi)\). Then the sixth roots of \(8\) are given as below:
$$\omega_{k}=\sqrt[6]{8}\{\cos \left(\frac{\pi+2k\pi}{6}+i\sin \frac{\pi+2k\pi}{6}\right)\}\ (k=0,1,2,3,4,5)$$
Therefore, we get
$$\begin{eqnarray*}\omega_{0}&=&8^{\frac{1}{6}}(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6})=\sqrt{2}\left(\frac{\sqrt{3}+i}{2}\right)\\\omega_{1}&=&8^{\frac{1}{6}}(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2})=\sqrt{2}i\\\omega_{2}&=&8^{\frac{1}{6}}(\cos \frac{5\pi}{6}+i\sin \frac{5\pi}{6})=\sqrt{2}\left(\frac{-\sqrt{3}+i}{2}\right)\\\omega_{3}&=&8^{\frac{1}{6}}(\cos \frac{7\pi}{6}+i\sin \frac{7\pi}{6})=\sqrt{2}\left(\frac{-\sqrt{3}-i}{2}\right)\\\omega_{4}&=&8^{\frac{1}{6}}(\cos \frac{3\pi}{2}+i\sin \frac{3\pi}{2})=-\sqrt{2}i\\\omega_{5}&=&8^{\frac{1}{6}}(\cos \frac{11\pi}{6}+i\sin \frac{11\pi}{6})=\sqrt{2}\left(\frac{\sqrt{3}-i}{2}\right)\\\end{eqnarray*}$$
Proof
We will find an nth root of the complex number \(z\), that is, a complex number \(\omega\) such that \(\omega^{n}=z\) .
Let \(z\) and \(\omega\) written as
$$\begin{eqnarray*}z&=&r(\cos \theta+i\sin \theta)\\\omega&=&s(\cos \lambda+i\sin \lambda)\end{eqnarray*}$$
Then, by De Moivre’s Theorem, we have
$$\omega^{n}=s^{n}(\cos n\lambda+i\sin n\lambda)=r(\cos \theta+i\sin \theta)\ \cdots (\text{*})$$
The equality of these two complex numbers shows that
$$\begin{eqnarray*}s^{n}&=&r\\ n\lambda&=&\theta+(2\pi\times k)\ (k\text{:integers})\end{eqnarray*}$$
since sine and cosine have period \(2\pi\).
Therefore, we get
$$\begin{eqnarray*}s&=&r^{\frac{1}{n}}\\\lambda&=&\frac{\theta+2k\pi}{n}\ (k=0,1,\cdots, n-1)\end{eqnarray*}$$
Thus, nth roots of the complex number z are given as follows:
$$\omega_{k}=r^{\frac{1}{n}}\left[\cos \left(\frac{\theta+2k\pi}{n}\right)+i\sin \left(\frac{\theta+2k\pi}{n}\right)\right]$$
where \(k=0,1,\cdots, n-1\).