Let \(z=f(x,y)\). Let \(dx\) and \(dy\) be small increments of \(x\) and \(y\), respectively. Then for these increments of \(x\) and \(y\), the corresponding change in \(z\) denoted by \(dz\), is given by
$$df : =f(x+dx, y+dy)-f(x,y)$$
The differential \(df=dz\) is also called the total differential and it also can be expressed by
$$df=f_{x}(x,y) dx +f_{y}(x,y) dy$$
where \(f_{x}(x,y)\) and \(f_{y}(x,y)\) are partial derivatives.
\(df\) represents the change in height of the surface when \(f\) changes from \((x,y)\) to \((x+dx, y+dy)\) and it is called a tangent plane. \(df\) is also denoted by \(dz\).Example
Let \(f(x,y)=x^{2}-y^{3}+5\).
Then, \(f_{x}(x,y)=2x\) and \(f_{y}(x,y)=-3y^{2}\).
Therefore, \(df=2x \cdot dx-3y^{2}\cdot dy\).
Geometric Interpretation
We explain why the differential is given by \(df=f_{x}(x,y) dx +f_{y}(x,y) dy\), by showing the geometric interpretation of the differential \(dz\) when the function is two variables.
First, we recall that the equation \(z=f(x,y)\) represent a surface as shown in Fig.
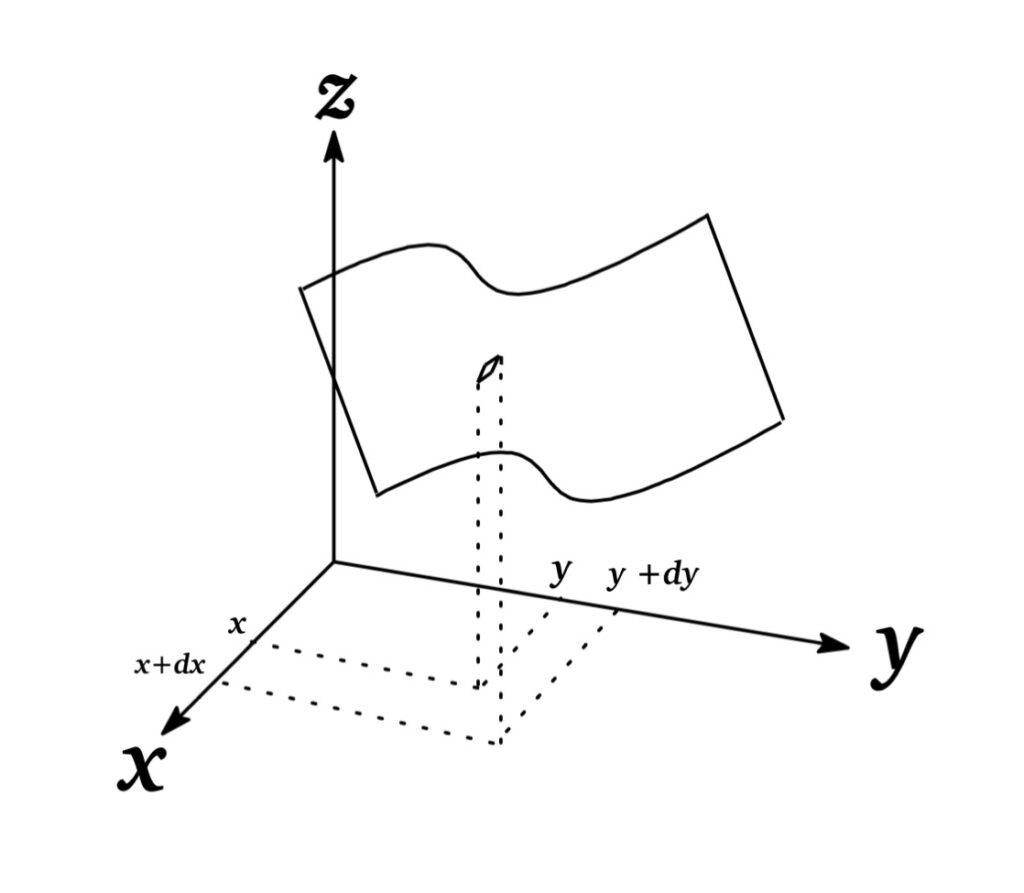

Then, as the partial derivatives, \(f_{x}(x,y)=\frac{\partial f}{\partial x}\) represents the rate of the change of \(f\) at \((x,y)\) with respect to x when \(y\) is fixed. Thus the point \(f(x+dx, y)\) which changes from \((x,y)\) to \((x+dx, y)\) is given by
$$f(x+dx, y)=f(x,y)+f_{x}(x,y)\cdot dx\ \ \ \cdots \ \ \ \text{(1)}$$
Similarly, the point \(f(x+dx, y+dy)\) which changes from \((x+dx,y)\) to \((x+dx, y+dy)\) is given by
$$f(x+dx, y+dy)=f(x+dx,y)+f_{y}(x+dx,y)\cdot dy\ \ \ \cdots \ \ \ \text{(2)}$$
where \(f_{y}(x+dx,y)=\frac{\partial f}{\partial x}\) represents the rate of the change of \(f\) at \((x+dx,y)\) with respect to y when \(x\) is fixed. Furthermore, if we notice that the slope of \(f_{y}(x+dx,y)\) is parallel to \(f_{y}(x,y)\) since it is a parallelogram when \(dx\) and \(dy\) are small.
Thus we can rewrite the equation (2) as below:
$$f(x+dx, y+dy)=f(x+dx,y)+f_{y}(x,y)\cdot dy\ \ \ \cdots \ \ \ \text{(2′)}$$
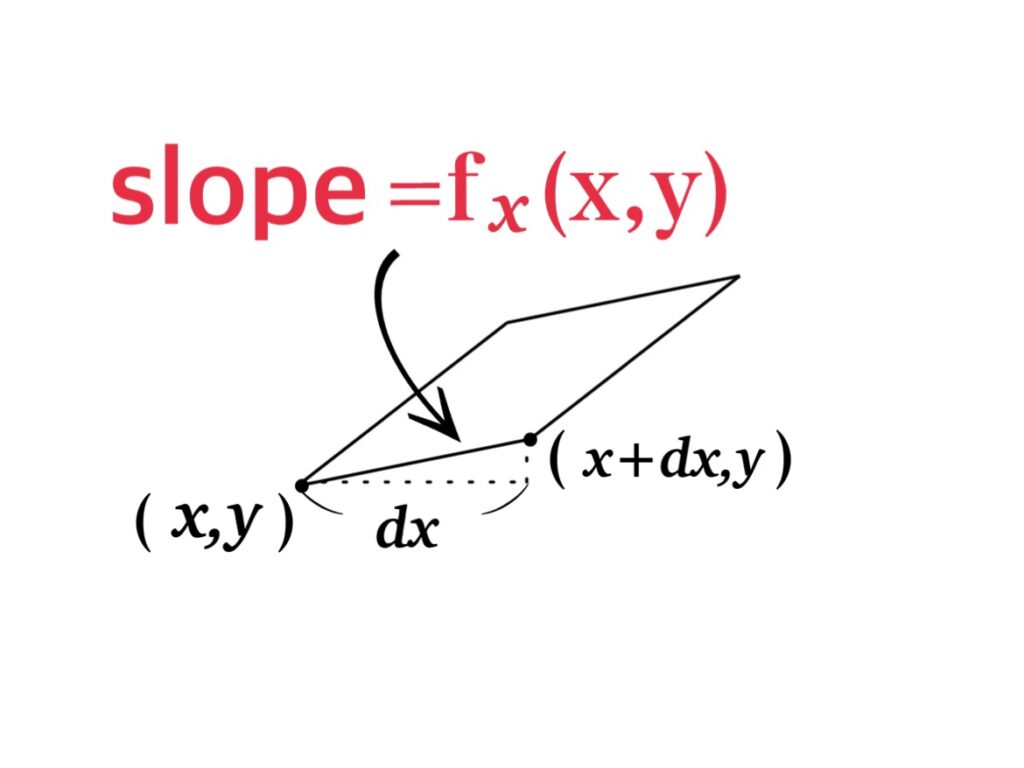

From (1) and (2′), we have
$$df=f(x+dx,y+dy)-f(x,y)=f_{x}(x,y) dx +f_{y}(x,y) dy$$
Functions of Three or More Variables
The definition of total differentials can be extended when the functions are three or more variables. For example. if \(u=f(x,y,z)\), we have the total differentials \(df=du\) is given by
$$df=f_{x}(x,y,z) dx +f_{y}(x,y,z) dy+f_{z}(x,y,z)$$
In general, if \(u=f(x_{1}, x_{2}, \cdots, x_{n})\) is a function of \(n\) variables, the total differential of \(df=du\) is given by
$$df=\displaystyle\sum_{k=1}^{n } f_{x_{k}}(x_{1}, x_{2}, \cdots, x_{n}) dx_{k} $$
where \(f_{x_{k}}(x_{1}, x_{2}, \cdots, x_{n})\) is the partial derivatives of \(f(x_{1}, x_{2}, \cdots, x_{n})\) with respect to \(x_{k}\).