$2$ 変数関数 $z=f(x,y)$ に対して, $f(x,y)$ の全微分 $df$ は$$df : =f(x+dx, y+dy)-f(x,y)$$で定義され, 偏微分 $f_{x}(x,y)$ と $f_{y}(x,y)$ を使って 次のようにあらわされる. $$df=f_{x}(x,y) dx +f_{y}(x,y) dy$$
$df$ は 関数 $f$ が $(x,y)$ から $(x+dx, y+dy)$ へそれぞれ $dx, dy$ だけ増加したときの $f$ の変化量(表面の高さの変化)を表し, 接線面と呼ばれます. (このとき $dx, dy$ はそれぞれ $x,y$ の微小増分を表す.)
また $df$ は $dz$ と表されることあらもある.一般に3変数関数以上の多変数関数になった場合も計算方法は同様.
Contents
例
例題 : \(f(x,y)=x^{2}-y^{3}+5\) の偏微分 $df$ を求めよ.
解答 : 偏微分 $f_{x}$ と $f_{y}$ は \(f_{x}(x,y)=2x\), \(f_{y}(x,y)=-3y^{2}\)で与えられるので
$$df=2x \cdot dx-3y^{2}\cdot dy$$
幾何的解釈
なぜ $2$ 変数関数の全微分 $df$ は \(df=f_{x}(x,y) dx +f_{y}(x,y) dy\) で与えられるのかを考えてみよう.
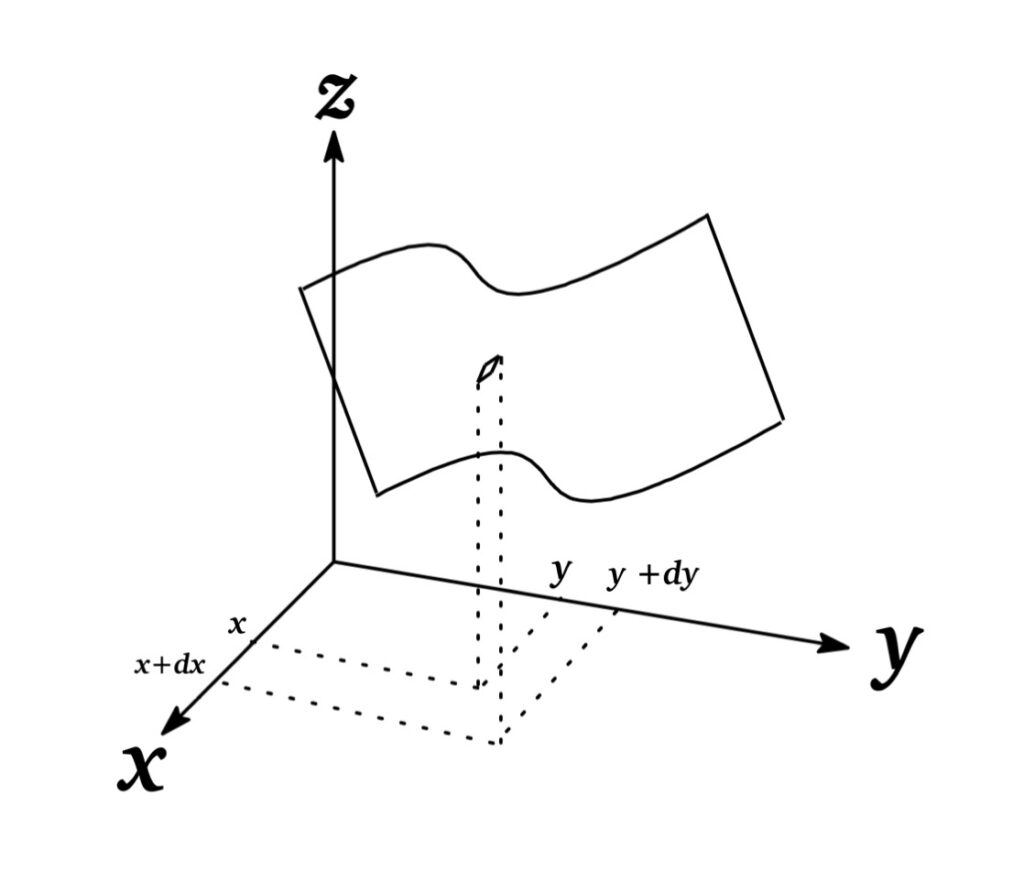
まず, 1変数関数のグラフは一般に曲線であったのに対し, 2変数関数 $z=f(x,y)$ は Fig のように曲面で表される。


このとき偏微分 $f_{x}(x,y)=\frac{\partial f}{\partial x}$ は $y$ を固定して(定数とみなしたうえで)$(x,y)$ における $x$に関する $f(x,y)$ の変化率を表している.
よって 座標 $(x,y)$ から $(x+dx, y)$ へ移った点 $f(x+dx, y)$ は 次のような式で与えらえる.
$$f(x+dx, y)=f(x,y)+f_{x}(x,y)\cdot dx\ \ \ \cdots \ \ \ \text{(1)}$$
同様に, 座標 \((x+dx,y)\) から \((x+dx, y+dy)\) へ移った点 $f(x+dx,y+dy)$ は次のような式で与えらえる.
$$f(x+dx, y+dy)=f(x+dx,y)+f_{y}(x+dx,y)\cdot dy\ \ \ \cdots \ \ \ \text{(2)}$$
このとき \(f_{y}(x+dx,y)=\frac{\partial f}{\partial x}\) は $x$ を固定して(定数とみなしたうえで)$(x+dx,y)$ における $f$ の変化率を表している.
注意:4 点 $(x,y), (x+dx,y), (x,y+dy), (x+dx, y+dy)$ は常に同一平面上にあるとは限らないが, $dx$ と $dy$ が微小である場合は同一平面上にあるとみなすことができるため, 4点は平行四辺形と形成する.
よって 4点 は 平行四辺形となるため, 傾き(Slope) \(f_{y}(x+dx,y)\) が \(f_{y}(x,y)\) に平行である.
以上より, 式(2) は次のように書き換えることができる:
$$f(x+dx, y+dy)=f(x+dx,y)+f_{y}(x,y)\cdot dy\ \ \ \cdots \ \ \ \text{(2′)}$$
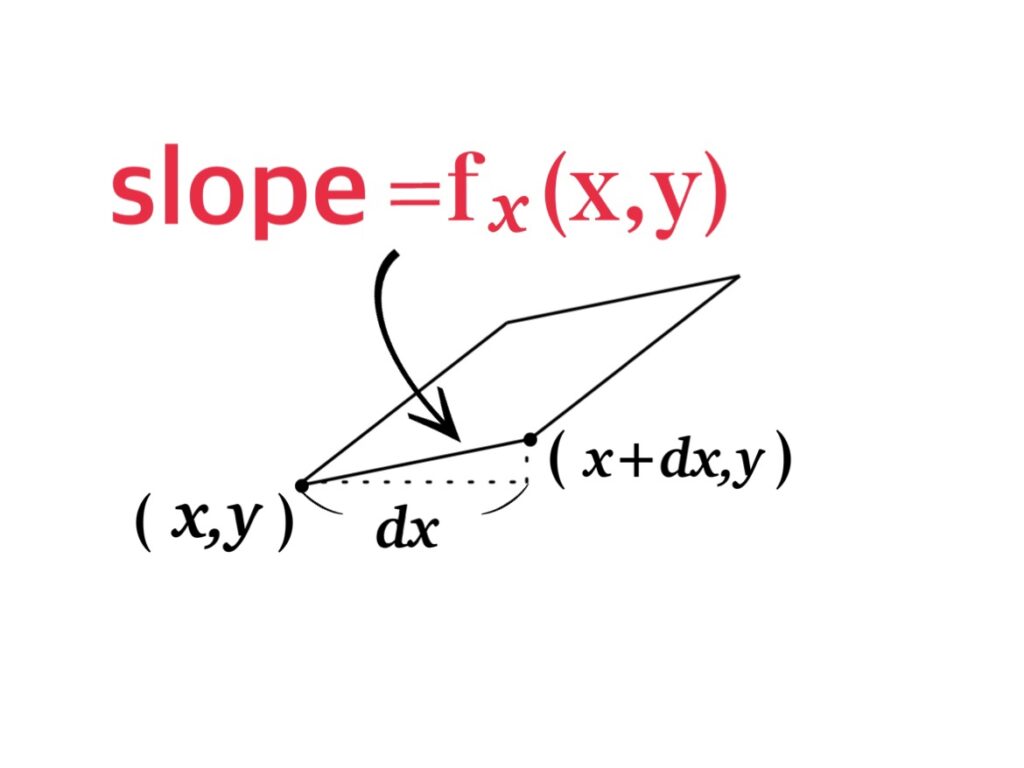

よって (1) と (2′) より, 次を得る.
$$df=f(x+dx,y+dy)-f(x,y)=f_{x}(x,y) dx +f_{y}(x,y) dy$$
3変数以上の多変数関数
全微分の定義は3変数以上の多変数関数の場合にも拡張することができる.
たとえば 3変数関数 \(u=f(x,y,z)\) が与えられたとき, 全微分 \(df=du\) は次のように表される.
$$df=f_{x}(x,y,z) dx +f_{y}(x,y,z) dy+f_{z}(x,y,z)$$
一般に $n$ 変数関数 \(u=f(x_{1}, x_{2}, \cdots, x_{n})\) の場合, 全微分 \(df=du\) は次のように与えられる.
$$df=\displaystyle\sum_{k=1}^{n } f_{x_{k}}(x_{1}, x_{2}, \cdots, x_{n}) dx_{k} $$
ただし \(f_{x_{k}}(x_{1}, x_{2}, \cdots, x_{n})\) は 変数 $x_{k}$ に関する 偏微分とする.