The Variance and Standard Deviation

Let X be a random variable. Then the variance and standard deviation of X are defined by

$$\text{Variance : } V[X]=E[\left(X-E[X]\right)^{2}]$$

$$\text{Standard Deviation : }\sqrt{V[X]}=\sqrt{E[\left(X-E[X]\right)^{2}]}$$

where $E[X]$ is the expectation of X.

As we have seen from the definition, the positive square root of the variance is the standard deviation.

The variance of $X$ is often denoted by $\sigma^{2}$ or $\sigma_{X}^{2}$, and the standard deviation of $X$ is often denoted by $\sigma$ or $\sigma_{X}$

Contents

1 Example
2 Significations
3 Properties
4 Discrete Case
5 Continuous Case

Example

The Table represents the values of X and the probability function.

Find the variance and the standard deviation of X.

Solution :

First, we find the expected value of X.

\begin{eqnarray*}E[X]&=&\sum_{x}\ x\cdot f(x)\\&=&1\times 0.1+2\times 0.4+3\times 0.3+5\times 0.1+6\times 0.1\\&=&2.9\end{eqnarray*}

Then the variance and the standard deviation of X are given as below:

$X$	$P(X=x)$ $=f(x)$
$1$	$0.1$
$2$	$0.4$
$3$	$0.3$
$4$	$0$
$5$	$0.1$
$6$	$0.1$
Others	$0$

\begin{eqnarray*}\text{variance : }V[X]&=&E[\left(X-E[X]\right)^{2}]=\sum_{i=1}^{6} (x_{i}-\mu)^{2}f(x_{i})\\&=&(1-2.9)^{2}\times 0.1+(2-2.9)^{2}\times 0.4+(3-2.9)^{2}\times 0.3+(5-2.9)^{2}\times 0.1+(6-2.9)^{2}\times 0.1\\&=&2.09\\\ \ \\\text{standard deviation : }&&\ \sqrt{V[X]}=\sqrt{2.09}\approx 1.45\end{eqnarray*}

Significations

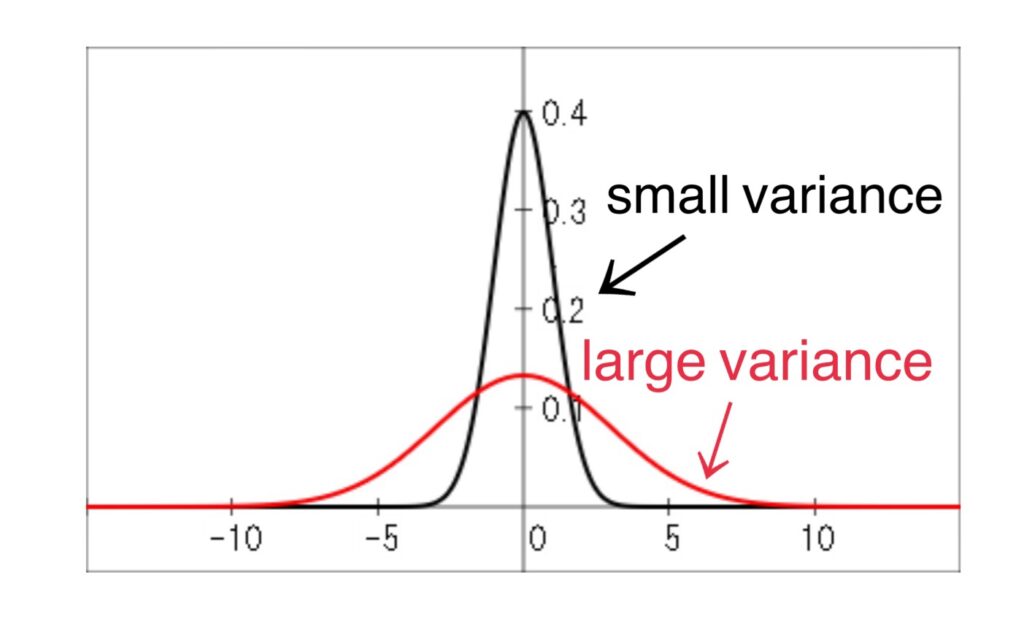
The variance is a measure of the dispersion, of the values of the random variable about the mean $\mu=E[X]$.

If the values tend to be concentrated near the mean, the variance is small. While if the values tend to be distributed far from the mean, the variance is large.

The Fig show the situation of the case of two distribution having the same mean $\mu=0$.

Properties

Let X and Y be random variables, and a and b be any constants.

$V[X]=E[\left(X-E[X]\right)^{2}]=E[X^{2}]-(E[X])^{2}$	Proof
$V[a]=0$	Proof
$V[aX]=a^{2}V[X]$	Proof
$V[aX+b]=a^{2}V[X]$	Proof
$V[aX+bY]=a^{2}V[X]+b^{2}V[Y]+2abCov[X,Y]$	Proof

Discrete Case

Suppose that X is a discrete random variable taking the values $x_{1}, x_{2}, \cdots ,x_{n}$ and having the probability function $ f(x)$. Then the variance is given by

$$V[X]=E[\left(X-E[X]\right)^{2}]=\sum_{i=1}^{n} (x_{i}-\mu)^{2}f(x_{i})$$

where where $E[X]=\mu$ is the expectation of X.

Continuous Case

Suppose that X is a continuous random variable having the probability function $ f(x)$. Then the variance is given by

$$V[X]=E[\left(X-E[X]\right)^{2}]=\int_{-\infty}^{\infty} (x-\mu)^{2}f(x)\ dx$$