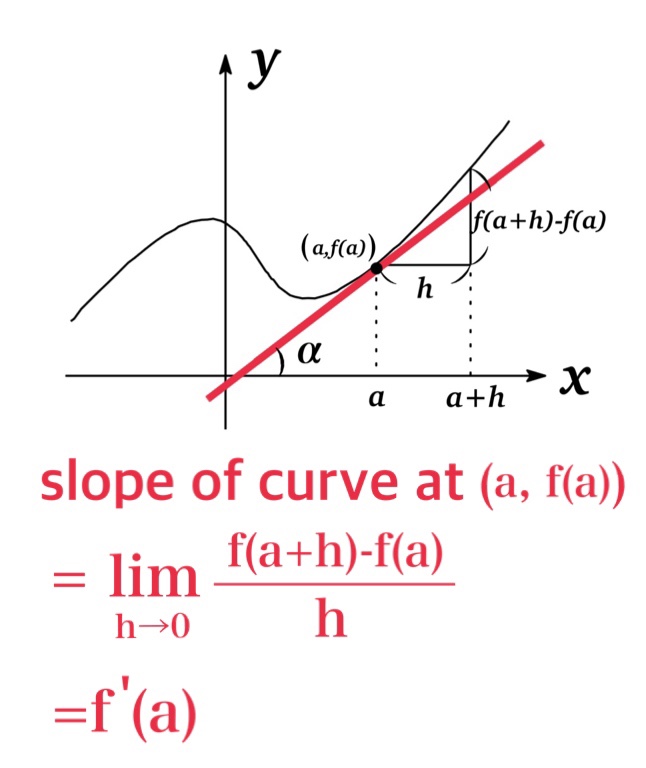
An equation of the tangent line to the curve \(f(x)\) at the point \((a,\ f(a))\) is given by
$$y-f(a)=f'(a)(x-a)$$
since the slope of a tangent line to \(y=f(x)\) at \(\left(a, f(a)\right)\) is equal to \(f'(a)\) which is the derivative of \(f\) at \(x=a\).
Let \(\alpha\) be the angle between \(x\)-axis and the tangent line where \(\). Then the slope of the tangent line is given by
$$f'(a)=\tan \alpha$$
Example
Find an equation of the tangent line to \(y=x^{2}+5x+7\) at the point \((2,3)\).
Solution: The derivative of \(y=x^{2}+5x+7\) is \(f'(x)=2x+5\). Therefore, the slope of the tangent line at \((2,3)\) is \(f'(2)=9\), and an equation of the tangent line is
$$y-3=(9)(x-2)\ \ \ \ \ \text{or}\ \ \ \ \ y=9x-15$$
Normal Line
The normal line to the curve \(f(x)\) at the point \((a,\ f(a))\) is the line passing through \((a,\ f(a))\) and perpendicular to the tangent line, given as follows:
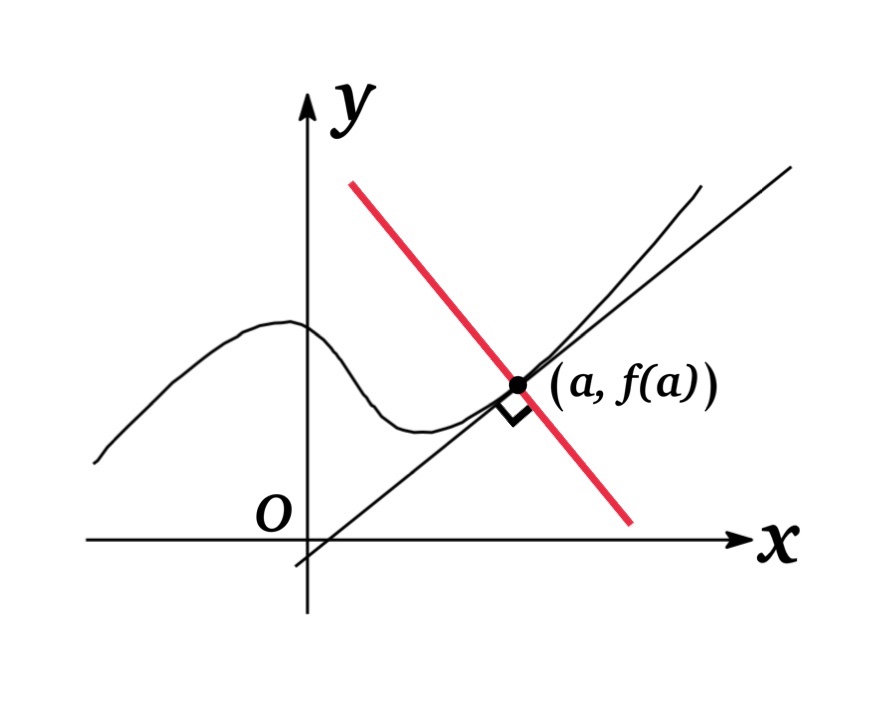
| \(f'(a)\) | Equation of Normal Line |
| \(f'(a)\not= 0\) | \(y-f(a)=-\frac{1}{f'(a)}(x-a)\) |
| \(f'(a)= 0\) | \(x=a\) |
Example
Find an equation of the normal line to \(y=x^{2}+5x+7\) at the point \((2,3)\).
Solution: We know that the derivative of \(y=x^{2}+5x+7\) at \((2,3)\) is \(f'(x)=2x+5\). Therefore, the slope of the normal line at \((2,3)\) is \(-\frac{1}{f'(2)}=-\frac{1}{9}\), and an equation of the tangent line is
$$y-3=(-\frac{1}{9})(x-2)\ \ \ \ \ \text{or}\ \ \ \ \ y=-\frac{x}{9}+\frac{15}{2}$$
Equations of Tangent Line
| \(y=f(x)\) | Tangent Line at \((x_{1},\ y_{1})\) | |
| General Expression | \(Ax^{2}+By^{2}=1\) | \(Ax_{1}x+By_{1}y=1\) |
| Circle | \(x^{2}+y^{2}=r^{2}\) | \(x_{1}x+y_{1}y=r^{2}\) |
| Ellipse | \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) | \(\frac{x_{1}x}{a^{2}}+\frac{y_{1}y}{b^{2}}=1\) |
| Hyperbola | \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) | \(\frac{x_{1}x}{a^{2}}-\frac{y_{1}y}{b^{2}}=1\) |
| Parabola | \(y^{2}=4px\) | \(y_{1}y=2p(x+x_{1})\) |