The product \(\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})\) is called the scalar triple product.
We can write the scalar triple product using the notation of determinants:
$$\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})=\left|\begin{array}{ccc}a_{1}& a_{2}& a_{3}\\b_{1}& b_{2}& b_{3}\\c_{1}& c_{2}& c_{3}\end{array}\right|$$
See also Cross Products (Section: Represented by the notation of determinants).
Geometric Interpretation
The magnitude of the scalar triple product \(|\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})|\) is equal to the volume of the parallelepiped determined by the vectors \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\).
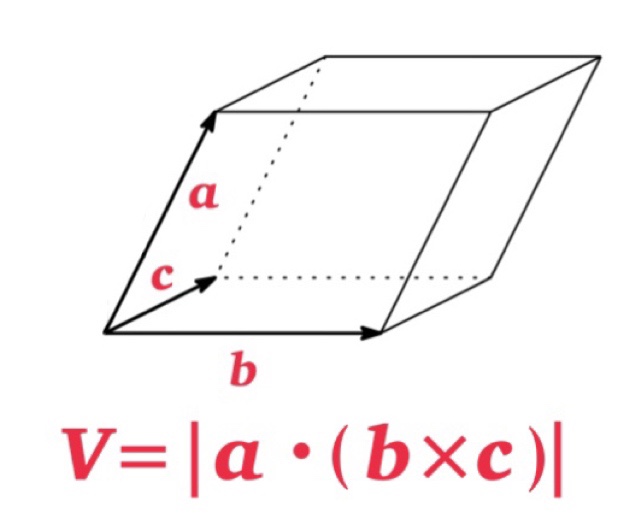
Notice that the volume of the parallelepiped is 0 if and only if the vectors lie in the same plane, and it is called coplanar.
See also dependent vectors.
Examples
Find the volume of the parallelepiped determined by the vectors \(\mathbf{a}=(1,2,3)\), \(\mathbf{b}=(4,5,6)\) and \(\mathbf{c}=(7,8,9)\).
$$\begin{eqnarray*}\mathbf{a}\cdot \mathbf{b}\times \mathbf{c}&=&\left|\begin{array}{ccc}1& 2& 3\\4& 5& 6\\7&8&9 \end{array}\right|\\&=&\left|\begin{array}{cc}5& 6\\ 8& 9\end{array}\right|\cdot 1-\left|\begin{array}{cc}4& 6\\7& 9\end{array}\right|\cdot 2+\left|\begin{array}{cc}4& 5\\ 7& 8\end{array}\right|\cdot 3\\&=&(-3)\cdot 1-(-6)\cdot 2+(-3)\cdot 3\\&=&0\end{eqnarray*}$$
Therefore the volume of parallelepiped determined by \(\mathbf{a}, \mathbf{b}\) and \(\mathbf{c}\) is 0, and this means that \(\mathbf{a}, \mathbf{b}\) and \(\mathbf{c}\) are coplanar.
Proof
The area of the base parallelogram is \(|\mathbf{b}\times \mathbf{c}|\). (See Geometric Interpretation of Cross Products.)
If \(\theta\) is the angle of \(\mathbf{a}\) and \(\mathbf{b}\times \mathbf{c}\), the height of the parallelepiped is given by (height)\(=|\mathbf{a}| |\cos\theta|\). (In case of \(\theta>\frac{\pi}{2}\), we use \(|\cos\theta|\).)
Therefore, the volume of the parallelepiped is represented as below:
$$\begin{eqnarray*}\text{Volume}&=&\text{(base area)}\times \text{(height)}\\&=&|\mathbf{b}\times \mathbf{c}| |\mathbf{a}| |\cos\theta|\\&=&|\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})|\end{eqnarray*}$$
