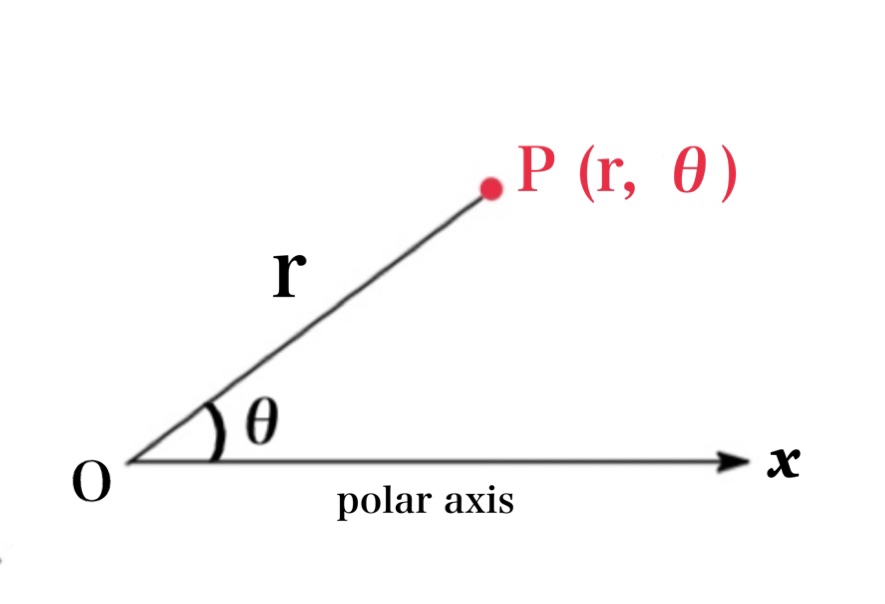
A point P in the plane represented by ordered pais \((r,\ \theta)\) is called a polar coordinate where r is the distance from O (pole or origin) and \(\theta\) is the angle (usually measured in radius) between the polar axis (x axis) and the line OP.
Notice that if P=O, then \(r=0\) and we agree that \((0, \theta)\) represents the pole (origin) for any value of \(\theta\).
Contents
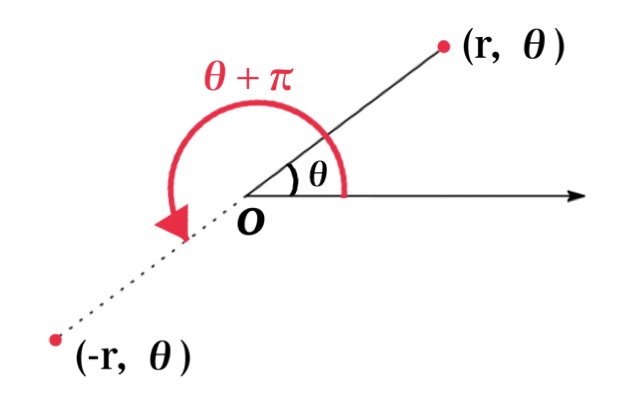
The case of r < 0
We can extend the polar coordinates \((r,\theta)\) to the case in which \(r\) is negative.
As shown in Figure , the points \((-r,\theta)\) and \((r,\theta)\) lie on the same line through \(O\) and at the same distance \(|r|\) from \(O\), but on the opposite sides of \(O\).
Therefore, we define that \((-r, \theta)\) represents the same point as \((r, \theta+\pi)\) where \(r\) > 0.
About representations of Polar coordinates
In the Cartesian coordinates system, every point has only one representation, but in the polar coordinate system each points has many representation.
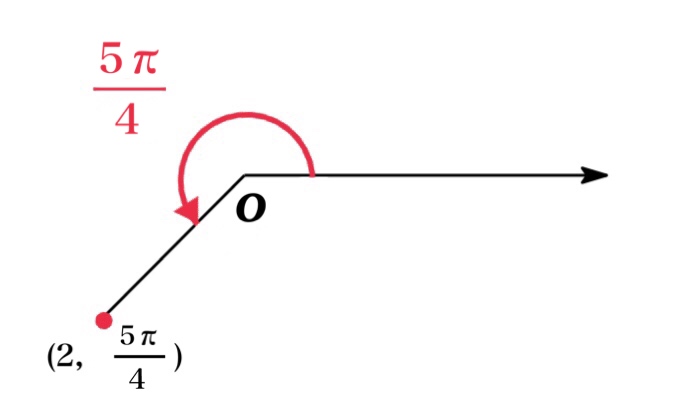
For instance, the point \((2, \frac{5\pi}{4})\) could be written as \((2, -\frac{3\pi}{4})\) or \((2, \frac{13\pi}{4})\) or \((-2, \frac{\pi}{4})\) and so on.
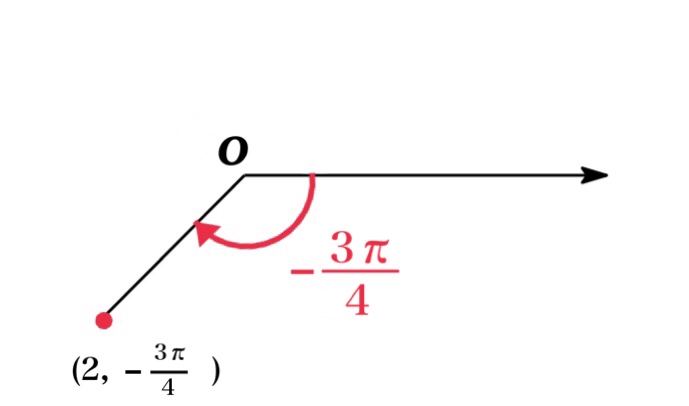
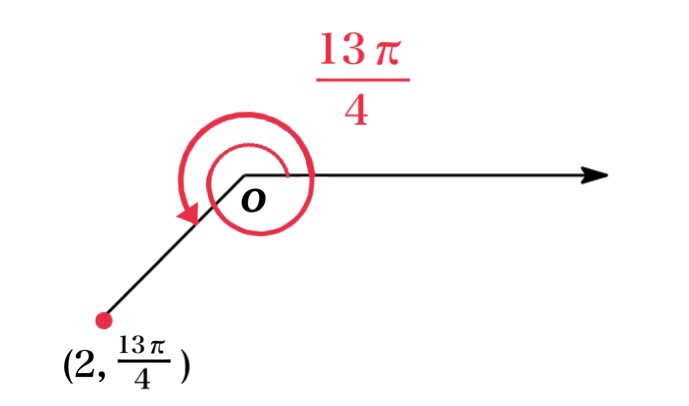
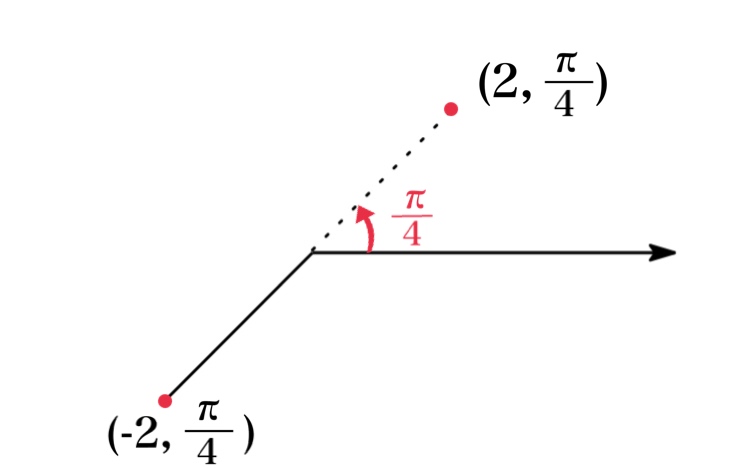
Generally, the point represented by polar coordinate \((r,\ \theta)\) is also represented by$$(r,\ \theta+2n\pi) \ \text{and} \ (-r,\ \theta+\pi+2n\pi)$$where \(n\) is any integer.
Transform
The connection between Polar and Cartesian coordinates can be seen in which the pole corresponds to the origin, and the polar axis coincides with the positive x-axis.
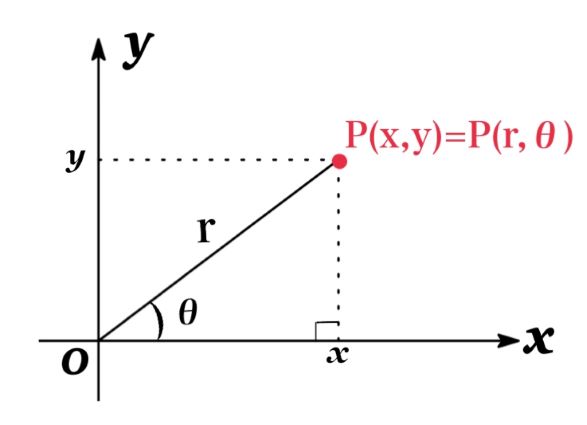
Polar coordinates → Cartesian coordinates
If the point P is given by Polar coordinate \((r,\ \theta)\), we can find x and y by the equations
$$\begin{eqnarray*}x&=&r\cos\theta \\y&=&r\sin\theta\end{eqnarray*}$$
Example: Covert the point \((2,\frac{5\pi}{4})\) from Polar to Cartesian coordinates.
Solution: Since \(r=2\) and \(\theta=\frac{5\pi}{4}\),
$$\begin{eqnarray*}x&=&r\cos\theta=2\cos \frac{5\pi}{4}=2\cdot -\frac{1}{\sqrt{2}}=-\sqrt{2} \\ y&=&r\sin\theta=2\sin \frac{5\pi}{4}=2\cdot -\frac{1}{\sqrt{2}}=-\sqrt{2}\end{eqnarray*}$$
Therefore, the point represented by Cartesian coordinates is \((-\sqrt{2}, -\sqrt{2})\).
Cartesian coordinates → Polar coordinates
If the point P is represented by Cartesian coordinates (x,y), we can find r and \(\theta\) by the equations
$$\begin{eqnarray*}&&r=\sqrt{x^{2}+y^{2}}\\&&\tan \theta=\frac{y}{x}\end{eqnarray*}$$
The equation above do not uniquely determine r and \(\theta\). Therefore, we can choose r>0 and \(0\leq \theta\)< \(2\pi\) generally.
Furthermore, to find \(\theta\) to satisfy the given point \((x,y)\), we must choose \(\theta\) so that the point lies in the correct quadrant as shown in the following example.
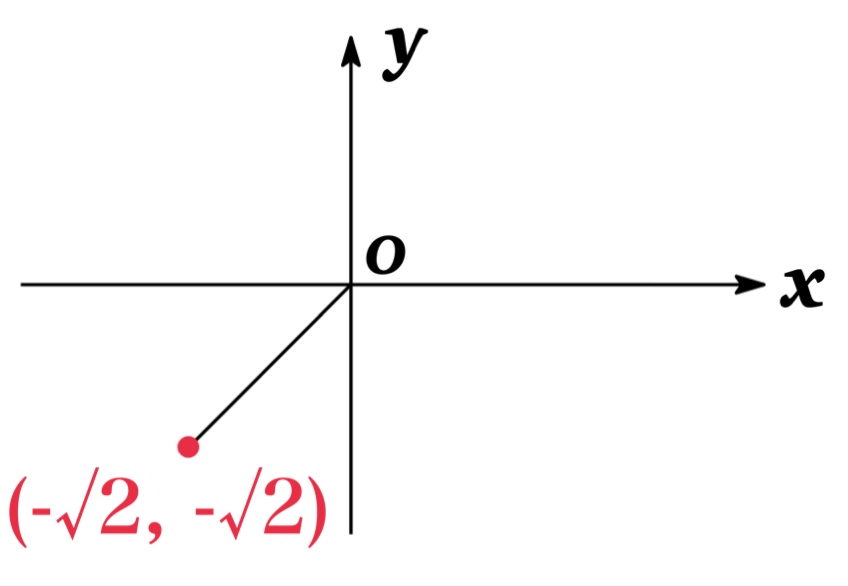
Example: Covert the point \((-\sqrt{2},-\sqrt{2})\) from Cartesian tp Polar coordinates.
Solution: Since \(x=-\sqrt{2}\) and \(y=-\sqrt{2}\),
$$\begin{eqnarray*}&&r=\sqrt{x^{2}+y^{2}}=\sqrt{(-\sqrt{2})^{2}+(-\sqrt{2})^{2}}=\sqrt{4}=2\\&&\tan \theta=\frac{y}{x}=\frac{-\sqrt{2}}{-\sqrt{2}}=1\end{eqnarray*}$$
If we choose \(\theta\) to be \(0\leq \theta <2\pi\), one possible answer is \(\theta=\frac{\pi}{4}\) or \(\theta=\frac{5\pi}{4}\).
However the point \((-\sqrt{2},-\sqrt{2})\) lies in the third quadrant, we must choose \(\theta=\frac{5\pi}{4}\).
Therefore, the point is \((2, \frac{5\pi}{4})\) in Polar coordinates.