2変数関数 $z=f(x, y)$ において
$$\begin{eqnarray*}&&\lim_{h\rightarrow 0}\frac{f(x+h,y)-f(x,y)}{h}\\&&\lim_{h\rightarrow 0}\frac{f(x,y+h)-f(x,y)}{h}\end{eqnarray*}$$
をそれぞれ $f(x,y)$ の $x$ と $y$ についての偏導関数といい$\frac{\partial }{\partial x}f(x,y),\ \frac{\partial }{\partial y}f(x,y)$ で表す.
$f(x,y)$ の $x$ についての 偏導関数 $\frac{\partial }{\partial x}f(x,y)$ は $y$ を固定して $f(x,y)$ を $x$ の1変数関数とみなして $x$ に関して微分したものである.
よって $x$ についての偏導関数の計算を行う場合は $f(x,y)$ において $y$ を定数とみなして(i.e. $f(x,y)$ を $x$ の1変数関数として )$x$ について微分すればよい.
同様に $y$ についての 偏導関数 $\frac{\partial }{\partial y}f(x,y)$ は $x$ を固定して $f(x,y)$ を $y$ の1変数関数とみなして $x$ に関して微分したものとなる.
また $f_{x}(x,y)$ は $y$ を固定して場合の $ f(x,y)$ の $x$ の変化量を表す.
偏導関数
例
$f(x,y)=x^{2}-y^{3}+5$ をそれぞれ $x$ について偏微分せよ.
定義に従い偏微分をすると
$$f_{x}(x,y)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x+h,y)-f(x,y)}{h}=\displaystyle\lim_{h\rightarrow 0}\frac{\left((x+h)^{2}-y^{3}+5\right)-\left(x^{2}-y^{3}+5\right)}{h}=\displaystyle\lim_{h\rightarrow 0}\frac{2hx+h^{2}}{h}=2x$$
または $y$ を定数として $x$ について微分すると
$$f_{x}(x,y)=2x$$
表記
偏微分にはいくつかの表記の仕方がある.
例えば \(z=f(x,y)\) の $x$ と $y$ についての偏微分には以下のようにいくつか書き方がある:
$$f_{x}(x,y)=f_{x}=\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}f(x,y)=\frac{\partial z}{\partial x}=D_{x}f$$
$$f_{y}(x,y)=f_{y}=\frac{\partial f}{\partial y}=\frac{\partial}{\partial y}f(x,y)=\frac{\partial z}{\partial y}=D_{y}f$$
偏微分係数
関数 $z=f(x, y)$ が $(a,b)\in D$ 上で定義されているとする. このとき
$$\begin{eqnarray*}&&\lim_{h\rightarrow 0}\frac{f(a+h,b)-f(a,b)}{h}\\&&\lim_{h\rightarrow 0}\frac{f(a,b+h)-f(a,b)}{h}\end{eqnarray*}$$
が存在するとき, この極限値をそれぞれ $f(x,y)$ の点$(a,b)$ における $x$ と $y$ についての偏微分係数といい$\frac{\partial f}{\partial x}(a,b),\ \frac{\partial f}{\partial y}(a,b)$ で表す.
1変数関数 $y=f(x)$ の場合, 微分係数 $f'(a)$ はグラフ上の点 $x=a$ における接線の傾きを表した.
2変数関数 $z=f(x,y)$ の場合, $f_{x}(a,b)$ は $x=a$ における $f(x,b)$ の接線の傾きを表している.
同様に $f_{y}(a,b)$ は $x=b$ における $f(x,b)$ の接線の傾きを表している.
詳細は次の幾何的解釈を参照.
幾何的解釈
$z=f(x,y)$ が与えられたとき, $z$ は曲面で表さる.
Fig.1 で表すように $z=f(x,y)$ の曲面上に $f(a,b)=c$ となるような点 $(a,b,c)$ を 取るとする.
ここで $y=b$ と固定して $f(x,b)$ について考えれば, $f(x,b)$ は $x$ の1変数関数になる.
このとき 1変数関数$f(x,b)$ は Fig.1 における曲線$C_{1}$で表される. ( 曲面 $z=f(x,y)$ を $y=b$ の断面図で切ったものが $f(x,b)$ となる.)
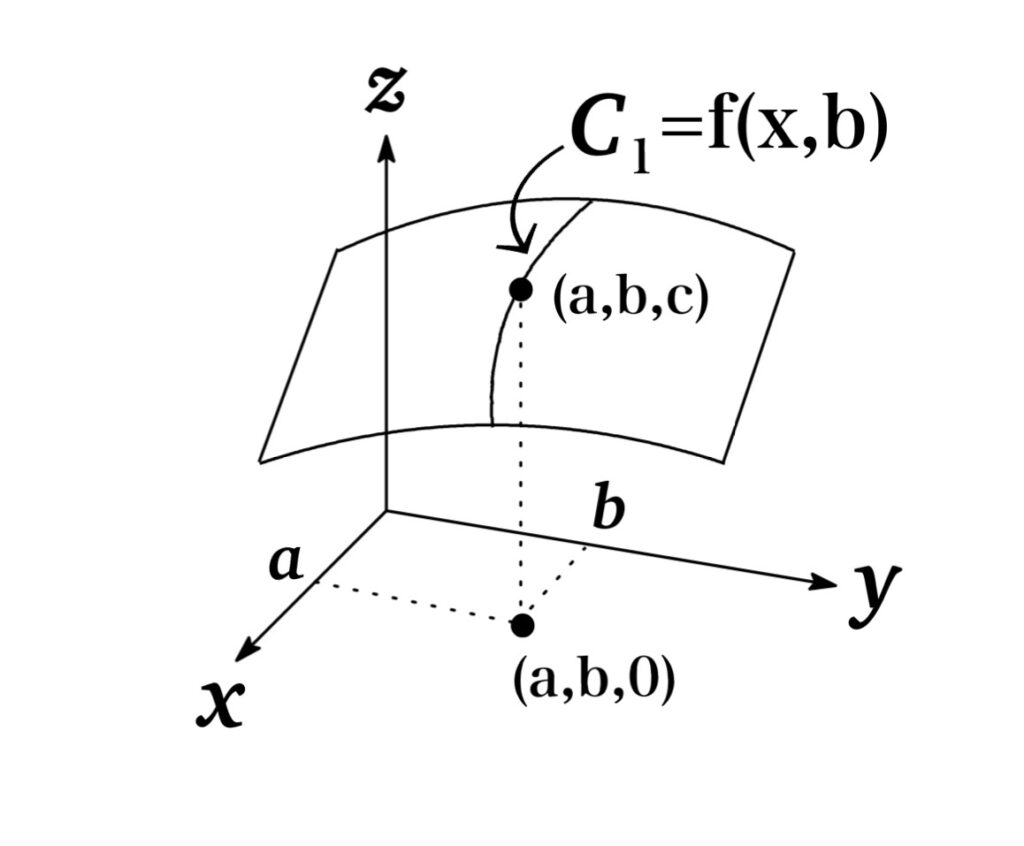
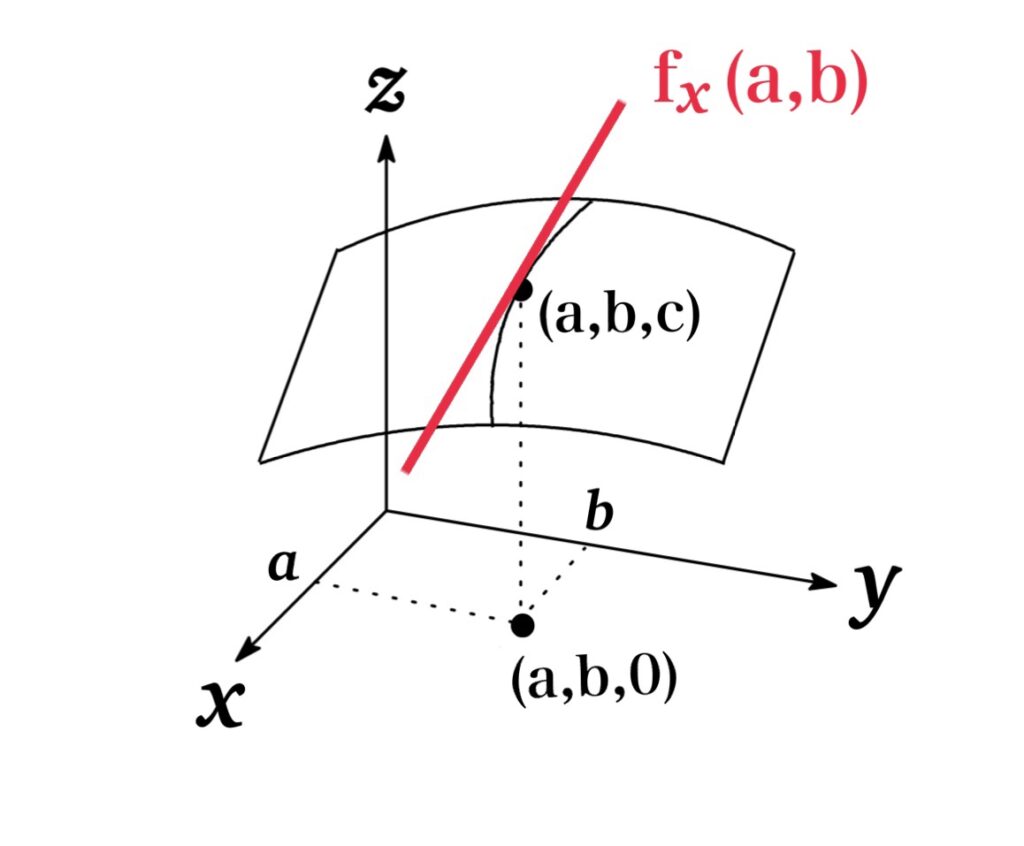
よって $x=a$ における $f(x,b)$ の接線の傾きは $\frac{d}{dx} f(x,b)|_{x=a}$ で得られる.
すなわち $f_{x}(a,b)$ は $x=a$ における $f(x,b)$ の接線の傾きを表している.
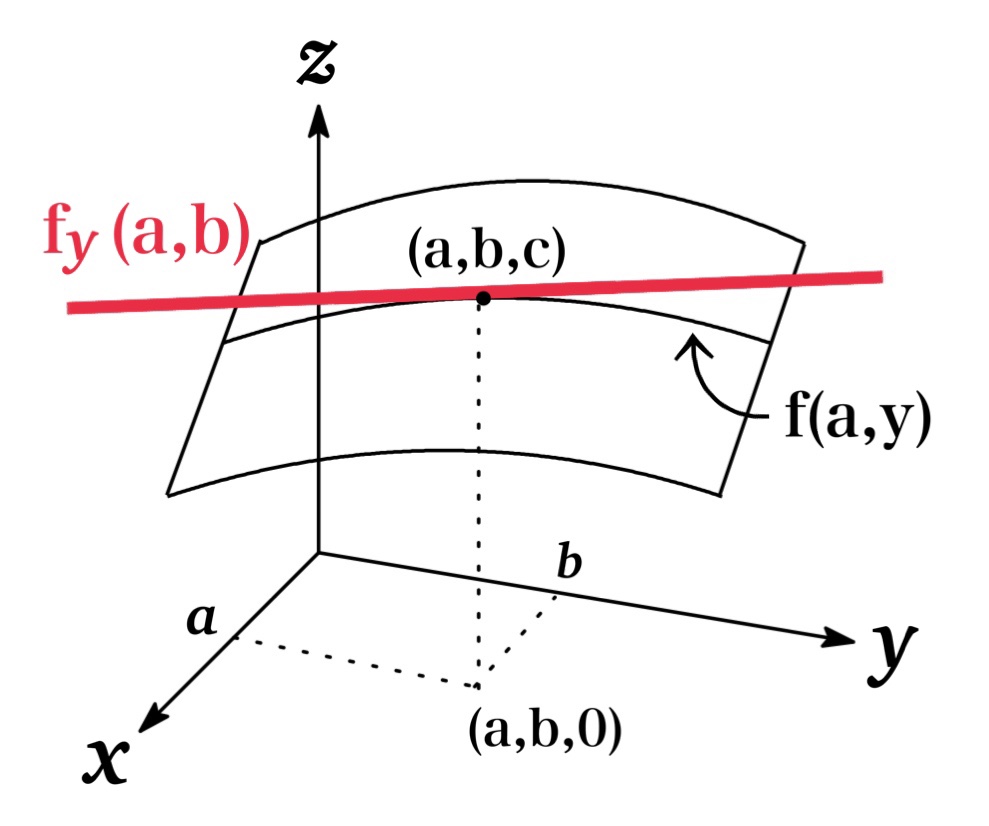
同様に偏微分係数 $f_{y}(a,b)$ は $x=a$ に固定した場合に$y$ の1変数関数 $f(a,y)$ に関して, $y=b$ における $f(a,y)$ の接線の傾きを表している.
3変数関数以上の多変数関数について
偏微分の定義は3変数以上の多変数関数についても同様に定義することができる.
3変数関数 $u=f(x, y, z)$ の $x,\ y,\ z$について偏導関数は以下で定義される.
$$f_{x}(x,y,z)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x+h,y,z)-f(x,y,z)}{h}$$
$$f_{y}(x,y,z)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x,y+h,z)-f(x,y,z)}{h}$$
$$f_{z}(x,y,z)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x,y,z+h)-f(x,y,z)}{h}$$
2変数関数の場合と同様に, $f_{x}(x,y,z)$ は $y$ と $z$ と固定して $x$ について偏微分したものとなる.
一般に $n$ 変数関数 $u=f(x_{1}, x_{2}, \cdots, x_{n})$ の場合, $x_{k}$ についての偏導関数は以下で与えられる:
$$f_{x_{k}}(x_{1},\cdots, x_{n})=\displaystyle\lim_{h\rightarrow 0} \frac{f(x_{1},\cdots, x_{k-1},x_{k}+h,x_{k+1},\cdots, x_{n})-f(x_{1},\cdots, x_{k},\cdots, x_{n})}{h}$$
また表記の仕方は以下のようになる:
$$f_{x_{k}}(x_{1},\cdots, x_{n})=f_{x_{k}}=\frac{\partial f}{\partial x_{k}}=\frac{\partial}{\partial x_{k}}f(x_{1},\cdots , x_{n})=\frac{\partial u}{\partial x_{k}}=D_{x_{k}}f$$