Let \(f(x,y)\) be a function of two variables. Then the parital derivatives of \(f\) with respect to x and y which are denoted by \(f_{x}(x,y)\) and \(f_{y}(x,y)\) respectively, are defined by
$$f_{x}(x,y)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x+h,y)-f(x,y)}{h}$$
$$f_{y}(x,y)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x,y+h)-f(x,y)}{h}$$
From the definition, we can see that the partial derivatives with respect to x is the ordinary derivatives of the function of single variable x while keeping y fixed. That is, we consider \(f(x,y)\) as a function of a single variable x, namely \(f(x,y)=g(x)\) where y is a constant.
Thus, to compute the partial derivatives with respect to x, regard y as a constant and differentiate \(f(x,y)\) with respect to x.
Similarly, the partial derivatives with respect to y is obtained by considering \(f(x,y)\) as the ordinary derivatives of the function of single variable y by keeping x fixed.
Notice that \(f_{x} (x,y)\) represents the rate of the change of \(f\) at \((x,y)\) with respect to x when \(y\) is fixed.
Similarly, \(f_{y}(x,y)\) represents the rate of the change of \(f\) at \((x,y)\) with respect to y when \(x\) is fixed.
Contents
Example
Let \(f(x,y)=x^{2}-y^{3}+5\). Then
$$f_{x}(x,y)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x+h,y)-f(x,y)}{h}=\displaystyle\lim_{h\rightarrow 0}\frac{\left((x+h)^{2}-y^{3}+5\right)-\left(x^{2}-y^{3}+5\right)}{h}=\displaystyle\lim_{h\rightarrow 0}\frac{2hx+h^{2}}{h}=2x$$
or considering y as a constant and differentiating with respect to x, we get easily
$$f_{x}(x,y)=2x$$
Notations
There are many alternative notations for partial derivatives. If \(z=f(x,y)\), we write
$$f_{x}(x,y)=f_{x}=\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}f(x,y)=\frac{\partial z}{\partial x}=D_{x}f$$
$$f_{y}(x,y)=f_{y}=\frac{\partial f}{\partial y}=\frac{\partial}{\partial y}f(x,y)=\frac{\partial z}{\partial y}=D_{y}f$$
We sometimes write \(f_{1}\) or \(D_{1}f\) instead of \(f_{x}\). This indicate differentiation with respect to the first variable \(x\). Thus, \(f_{2}\) or \(D_{2}f\) indicates the differentiation with respect to the second variable \(y\).
Higher Derivatives
Let \(f(x,y)\). Then we can consider the partial derivatives of \(f_{x}\) and \(f_{y}\), which are called the second partial derivatives of \(f(x,y)\). For example, the partial derivatives of \(f_{x}\) with respect to x and y are given as below:
$$(f_{x})_{x}=f_{xx}=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^{2} f}{\partial x^{2}}=\frac{\partial^{2} z}{\partial x^{2}}$$
$$(f_{x})_{y}=f_{xy}=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^{2} f}{\partial y \partial x}=\frac{\partial^{2} z}{\partial y \partial x}$$
As we have seen, the notation \(f_{xy}\) or \(\frac{\partial^{2} }{\partial y\partial x}\) means that we first differentiate with respect to x and then with respect to y. whereas in computing \(f_{yx}\) the order is reversed.
Example
Let \(f(x,y)=x^{2}-y^{3}+5\). Then
$$f_{x}(x,y)=2x$$
$$f_{xx}(x,y)=2$$
$$f_{xy}(x,y)=0$$
Geometric Interpretation
To see a geometric interpretation of partial derivatives, we first recall that the equation of \(z=f(x,y)\) represents a surface.
If \(f(a,b)=c\), then the point (a,b,c) lies on the Surface as shown in Fig 1.
Then, by fixing \(y=b\), we can attention to the change of \(x\) represented by \(g(x)=f(x,b)\).
The graph of \(g(x)=f(x,b)\) is the curve \(C_{1}\), the trace of S in the plane \(y=b\).
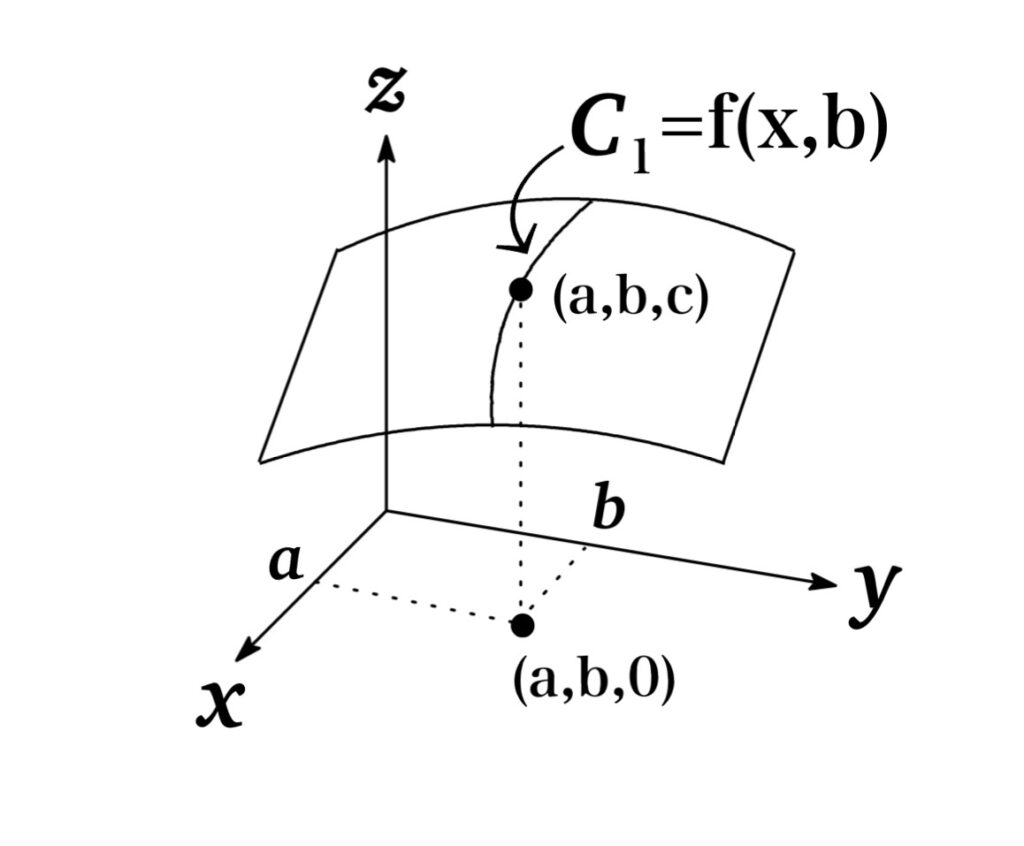
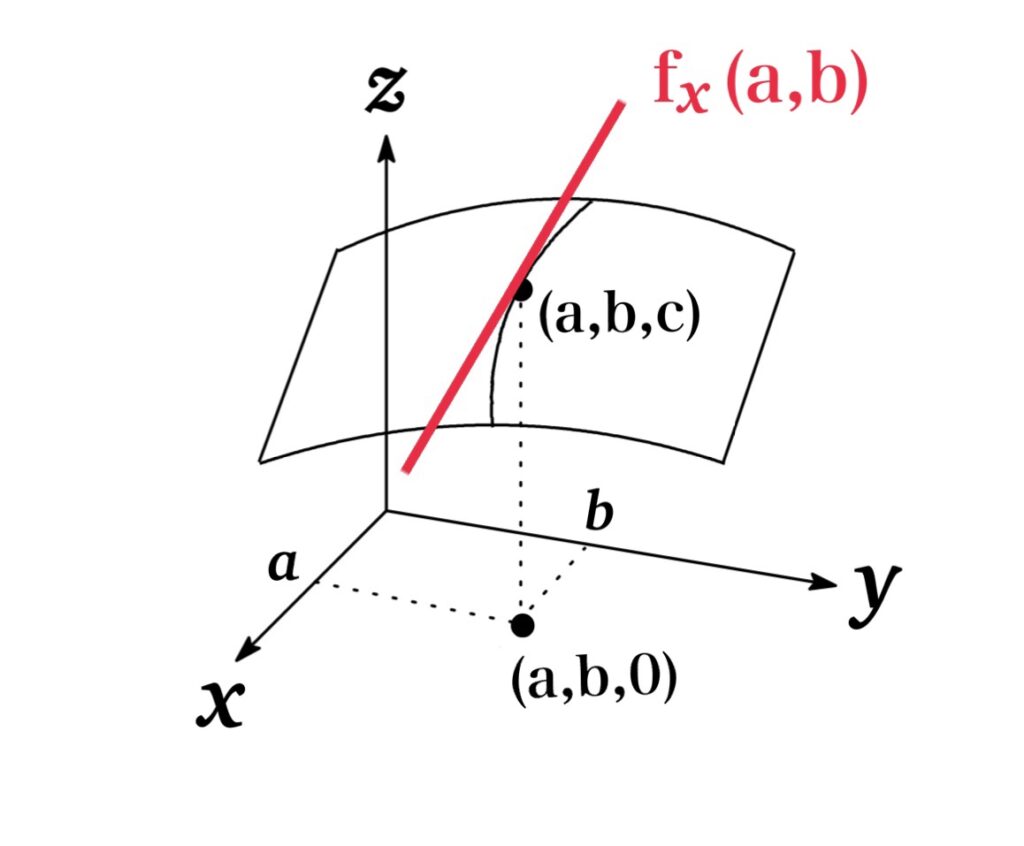
Therefore, the slope of its tangent line at \((a,b,c)\) is \(g'(a)=f_{x}(a,b)\).
Thus the partial derivatives \(f_{x}(a,b)\) can be interpreted geometrically as the slope of the tangent line at \((a,b,c)\) to the \(g(x)=f(x,b)\).
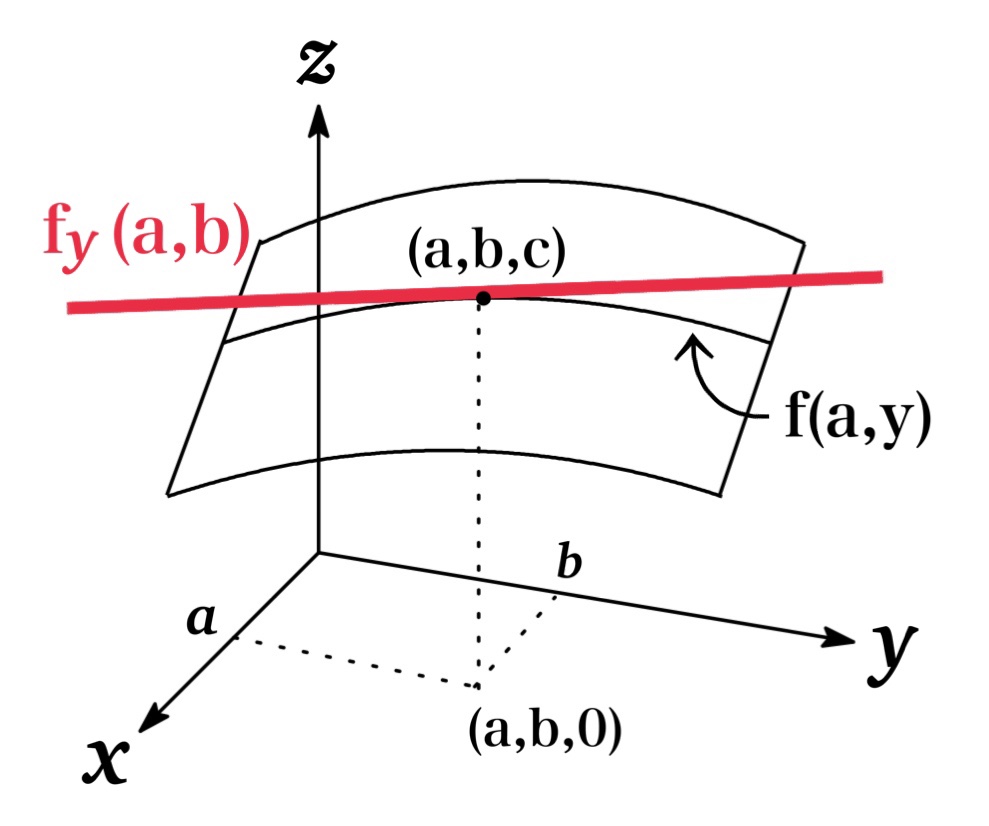
Similarly we can give a geometric interpretation to the partial derivatives \(f_{y}\) as shown in Fig 3.
Functions of Three or More Variables
The definition of partial differentials can be extended when the functions are three or more variables. For example, if \(u=f(x,y,z)\), we have the partial differentials with respect to \(x\), \(y\) and \(z\)
$$f_{x}(x,y,z)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x+h,y,z)-f(x,y,z)}{h}$$
$$f_{y}(x,y,z)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x,y+h,z)-f(x,y,z)}{h}$$
$$f_{z}(x,y,z)=\displaystyle\lim_{h\rightarrow 0} \frac{f(x,y,z+h)-f(x,y,z)}{h}$$
Similar to the function of two variables, \(f_{x}(x,y,z)\) represents the rate of the change of \(f\) at \((x,y,z)\) with respect to x when \(y\) and \(z\) are fixed.
In general, if \(u=f(x_{1}, x_{2}, \cdots, x_{n})\) is a function of \(n\) variables, its partial derivatives with respect to the \(x_{k}\) where \(1\leq k\leq n\) is given by
$$f_{x_{k}}(x_{1},\cdots, x_{n})=\displaystyle\lim_{h\rightarrow 0} \frac{f(x_{1},\cdots, x_{k-1},x_{k}+h,x_{k+1},\cdots, x_{n})-f(x_{1},\cdots, x_{k},\cdots, x_{n})}{h}$$
and we have notations as below:
$$f_{x_{k}}(x_{1},\cdots, x_{n})=f_{x_{k}}=\frac{\partial f}{\partial x_{k}}=\frac{\partial}{\partial x_{k}}f(x_{1},\cdots , x_{n})=\frac{\partial u}{\partial x_{k}}=D_{x_{k}}f$$
Related Articles
See also