対数関数

$a\not= 1$ かつ $a>0$ とする. このとき任意の整数 $M$ に対して $M=a^{p}$ となる実数 $p$ がただ一つ定まる.
この $p$ を $p=\log_{a} M$ で表す. すなわち
$$p=\log_{a} M\ \ \ \ \Longleftrightarrow\ \ \ \ \ a^{p}=M$$
また $p=\log_{a} M$ を $a$を底とする $p$ の対数といい, $M$ を真数という.

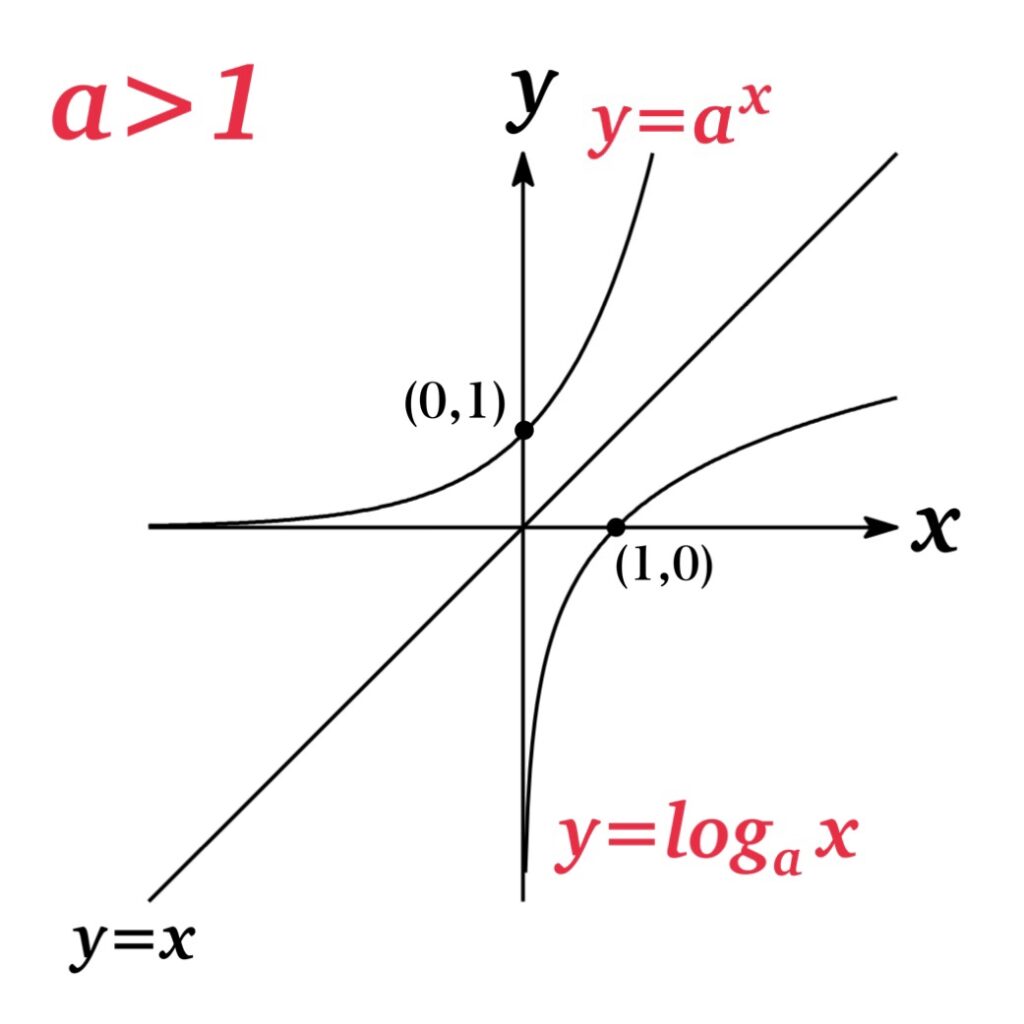
$a>0$ かつ $a\not= 1$ より, $f(x)=a^{x}$ は単調関数であるので, 逆関数が定義される.

すなわち, $f(x)=\log x$ とするとき, 逆関数は $f^{-1}(x)=a^{x}$ で与えれる.

→逆関数について

Contents

1 例
2 対数法則
3 グラフ
4 常用対数・自然対数
5 導関数
- 5.1 自然対数
- 5.2 対数関数
6 対数微分法
- 6.1 例
7 テイラー展開

例

$\log_{2} 8=3 $　（なぜなら $2^{3}=8$）
$\log_{8} 2=\frac{1}{3}$　（なぜなら $8^{\frac{1}{3}}=2$ ）
$\log_{10} 0.01=-2 $ 　（なぜなら $10^{-2}=\frac{1}{10^{2}}=0.01$）

対数法則

$a>0$ かつ $a\not= 1$ とする.

性質	例
$\log_{a} 1=0$	$\log_{3} 1=0$
$\log_{a} a^{x}=x$	$\log_{2}8=\log_{2} 2^{3}=3$
$a^{\log_{a} x}=x$	$3^{\log_{3} 5}=5$
$\log_{a} (xy)=\log_{a}x+\log_{a}y$	$\log_{3} 35=\log_{3}5+\log_{3}7$
$\log_{a} \left(\frac{x}{y}\right)=\log_{a}x-\log_{a}y$	$\log_{3} \left(\frac{7}{5}\right)=\log_{3}7-\log_{3}5$
$\log_{a} x^{r}=r\log_{a}x$	$\log_{3} \sqrt{5}=\frac{1}{2}\log_{3}5$
$\log_{a} x=\frac{\log_{c}x}{\log_{c}a}$	$\log_{4} 9=\frac{\log_{2}9}{\log_{2}4}=\frac{1}{2}\log_{2}9=\log_{2}3$
$a^{\log_{b}c}=c^{\log_{b}a}$	$4^{\log_{2}3}=3^{\log_{2}4}=3^{2}=9$
$(\log_{a} b)(\log_{b} c)=\log_{a}c$	$(\log_{2} 3)(\log_{3} 5)=\log_{2}5$
$\log_{a^{n}} b=\frac{1}{n}\log_{a}b$	$\log _{8} 5=\log_{2^{3}} 5=\frac{1}{3}\log_{2} 5$

グラフ

	単調増加 / 単調減少
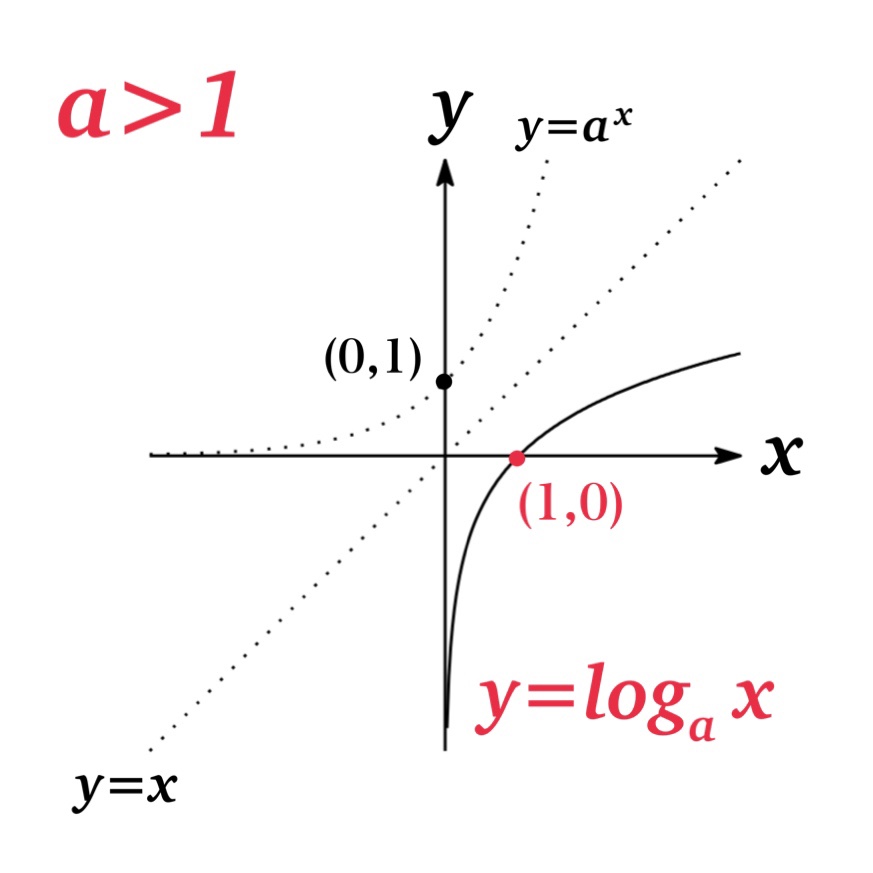
a>1 (Fig.1)	$f(x)=\log_{a} x$ は単調増加関数	$ 0< x_{1}< x_{2}\ \ \ \leftrightarrow\ \ \ \log_{a} x_{1}<\log_{a} x_{2}$
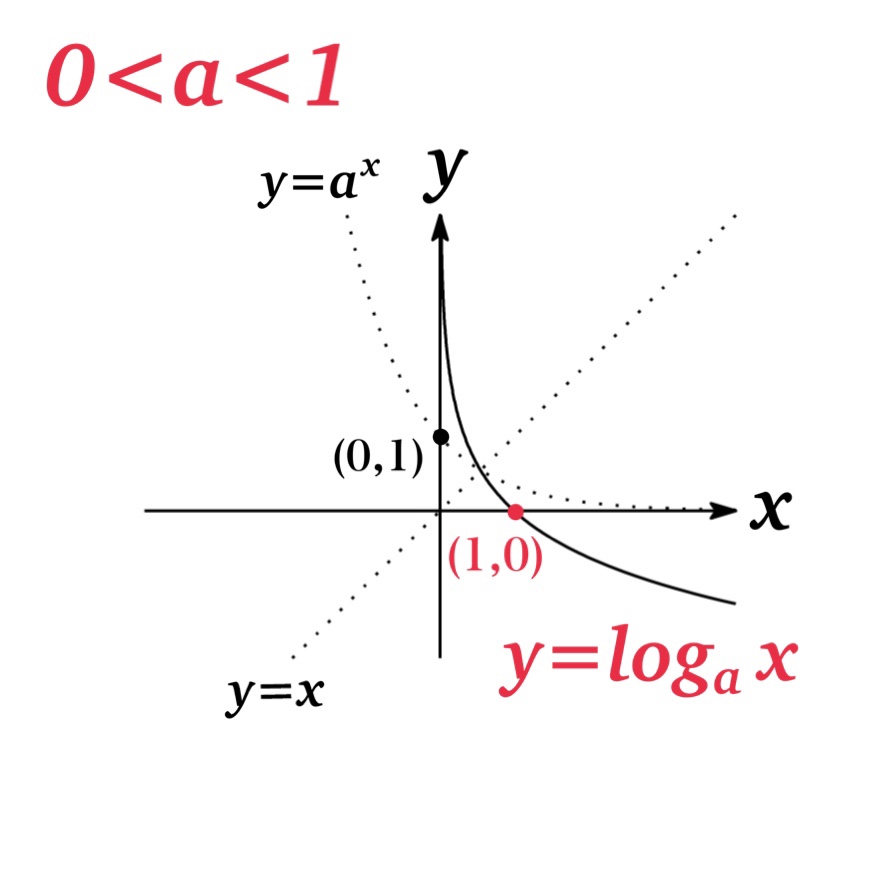
0<a<1 (Fig.2)	$f(x)=\log_{a} x$ は単調減少関数	$ 0< x_{1}< x_{2}\ \ \ \leftrightarrow\ \ \ \log_{a} x_{2}<\log_{a} x_{1}$

$y=\log_{a} x$ は $y=a^{x}$ の逆関数であるので, $y=x$ について対称となっている.

常用対数・自然対数

底を $a=10$ とする対数関数 $y=\log_{10} x$ を常用対数といい, $10$ を省略して次のように書くこともある：

$$\log_{\mathrm{10}} x=\log x$$

また底を $a=\mathrm{e}$ とする対数関数 $y=\log_{e} x$ を自然対数といい, これを次のように書く：

$$\log_{\mathrm{e}} x=\ln x$$

注記：ここで $\mathrm{e}=2.7818\cdots $ はネイピア数と呼ばれる定数で極限値 : $\mathrm{e}=\displaystyle\lim_{x\rightarrow 0} (1+x)^{\frac{1}{x}}$ で定義される.

導関数

自然対数

自然対数 $y=\log_{e} x$ の導関数は次で与えらえる：
$(1)\ \ \frac{d}{dx}\log_{\mathrm{e}} x=\frac{1}{x}$
$(2)\ \ \frac{d}{dx} \log_{\mathrm{e}} f(x)=\frac{f'(x)}{f(x)}$

証明（１）：微分法の定義に従えば

$\begin{eqnarray*}\frac{d}{dx}\log_{e} x&=&\displaystyle\lim_{h\rightarrow 0}\frac{\log_{e} (x+h)-\log_{e} x}{h}\\&=&\displaystyle\lim_{h\rightarrow 0}\frac{1}{h}\log_{e} \frac{x+h}{x}\\&=&\displaystyle\lim_{h\rightarrow 0}\frac{1}{x}\cdot \frac{x}{h}\log_{e} (1+\frac{h}{x})\\&=&\displaystyle\lim_{h\rightarrow 0}\frac{1}{x}\log_{e} \left(1+\frac{h}{x}\right)^{\frac{h}{x}}\\&=&\frac{1}{x}\log_{e} e\\&=&\frac{1}{x}\end{eqnarray*}$

注記： $\mathrm{e}^{y}=x\ \ (\text{すなわち} y=\log x)$ の両辺をそれぞれ $x$ について微分すれば次を得る：

$$\mathrm{e}^{y} \frac{dy}{dx}=1$$

よって

$$\frac{dy}{dx}=\frac{1}{\mathrm{e}^{y}}=\frac{1}{x}$$

証明（２）：合成関数の微分法を用いればよい.

対数関数 $y=\log_{a} x$ の導関数は次で与えらえる：
$$\frac{d}{dx} \log_{a} x=\frac{1}{x\log_{e} a}$$

証明：対数法則 $\log_{a} x=\frac{\log_{c}x}{\log_{c}a}$ を利用する.

$$\frac{d}{dx}(\log_{a} x)=\frac{d}{dx}\left(\frac{\log_{\mathrm{e}}x}{\log_{\mathrm{e}}a}\right)=\frac{1}{\log_{\mathrm{e}}a}\frac{d}{dx}(\log_{\mathrm{e}}x)=\frac{1}{\log_{\mathrm{e}}a}\cdot \frac{1}{x}$$

対数微分法

関数 $y=f(x)$ が与えられたとき,両辺の対数をとって微分を行う方法を対数微分という.

そのままの形でも微分はできる場合でも, 複雑な関数の積や商, 累乗を含むとき, 両辺の対数をとることにより, 累乗は対数の係数に, 積・商はそれぞれ対数の和・差で表せるので, 微分を行うのが簡単になる.

(Step 1)　両辺の対数をとる.
(Step 2)　両辺を $x$ で微分する.
(Step 3)　$y’$について解く.

例

$y=\frac{x^{\frac{1}{3}}\sqrt{x^{2}+1}}{(3x+2)^{3}}$ を対数微分法を用いて微分せよ.

(Step1) 両辺の対数をとる.

$$\ln y=\frac{1}{3}\ln x+\frac{1}{2}\ln (x^{2}+1)-3\ln (3x+2)$$

(Step 2) $x$ について両辺を微分する.

$$\frac{1}{y}\frac{dy}{dx}=\frac{1}{3}\cdot \frac{1}{x}+\frac{1}{2}\cdot \frac{2x}{x^{2}+1}-3\cdot\frac{3}{3x+2}$$

(Step 3) $\frac{dy}{dx}$ について解く.

$$\begin{eqnarray*}\frac{dy}{dx}&=&y\left(\frac{1}{3x}+ \frac{x}{x^{2}+1}-\frac{9}{3x+2}\right)\\&=&\frac{x^{\frac{1}{3}}\sqrt{x^{2}+1}}{(3x+2)^{3}}\left(\frac{1}{3x}+ \frac{x}{x^{2}+1}-\frac{9}{3x+2}\right)\end{eqnarray*}$$

テイラー展開

$\log_{e} x$ を $x=1$ のまわりでテイラー展開すると以下で得られる：
$$\log_{e} x=\displaystyle \sum_{n=1}^{\infty}(-1)^{n}\frac{(x-1)^{n}}{n} $$

$x>0$ が定義域なので, $x=0$ でテイラー展開はできないことに注意する.

証明：$f(x)=\log_{e} x$とおく. このとき

$\begin{eqnarray*}f^{(n)}(x)&=&(-1)^{n}\frac{(n-1)!}{x^{n}}\\f^{(n)}(1)&=&(-1)^{n}(n-1)!\end{eqnarray*}$

よって $x=1$ のまわりで $f(x)=\log_{e} x$ のテイラー展開は次で与えられる：

$\begin{eqnarray*}f(x)&=&\displaystyle \sum_{n=0}^{\infty} f^{n}(1)\frac{(x-1)^{n}}{n!}\\&=&\displaystyle \sum_{n=0}^{\infty}(-1)^{n}\frac{(n-1)!}{n!}(x-1)^{n}\\&=&\displaystyle \sum_{n=1}^{\infty}(-1)^{n}\frac{(x-1)^{n}}{n} \end{eqnarray*}$

微積分

性質	例
\(\log_{a} 1=0\)	\(\log_{3} 1=0\)
\(\log_{a} a^{x}=x\)	\(\log_{2}8=\log_{2} 2^{3}=3\)
\(a^{\log_{a} x}=x\)	\(3^{\log_{3} 5}=5\)
\(\log_{a} (xy)=\log_{a}x+\log_{a}y\)	\(\log_{3} 35=\log_{3}5+\log_{3}7\)
\(\log_{a} \left(\frac{x}{y}\right)=\log_{a}x-\log_{a}y\)	\(\log_{3} \left(\frac{7}{5}\right)=\log_{3}7-\log_{3}5\)
\(\log_{a} x^{r}=r\log_{a}x\)	\(\log_{3} \sqrt{5}=\frac{1}{2}\log_{3}5\)
\(\log_{a} x=\frac{\log_{c}x}{\log_{c}a}\)	\(\log_{4} 9=\frac{\log_{2}9}{\log_{2}4}=\frac{1}{2}\log_{2}9=\log_{2}3\)
\(a^{\log_{b}c}=c^{\log_{b}a}\)	\(4^{\log_{2}3}=3^{\log_{2}4}=3^{2}=9\)
\((\log_{a} b)(\log_{b} c)=\log_{a}c\)	\((\log_{2} 3)(\log_{3} 5)=\log_{2}5\)
\(\log_{a^{n}} b=\frac{1}{n}\log_{a}b\)	\(\log _{8} 5=\log_{2^{3}} 5=\frac{1}{3}\log_{2} 5\)

	単調増加 / 単調減少
a>1 (Fig.1)	\(f(x)=\log_{a} x\) は単調増加関数	\( 0< x_{1}< x_{2}\ \ \ \leftrightarrow\ \ \ \log_{a} x_{1}<\log_{a} x_{2}\)
0<a<1 (Fig.2)	\(f(x)=\log_{a} x\) は単調減少関数	\( 0< x_{1}< x_{2}\ \ \ \leftrightarrow\ \ \ \log_{a} x_{2}<\log_{a} x_{1}\)