関数 $f(x, y)$ において, $(x,y)$ が $(a,b)$ と異なる値を取りながら限りなく $c$ に近づくとき
$$\displaystyle\lim_{(x,y)\rightarrow (a,b)}f(x,y)=c$$
と表し, $c$ を $(x,y)\rightarrow (a,b)$ のときの $f(x,y)$ の極限値であるという.
ここで$(a,b)$ が限りなく $c$ に近づくとは, $(x,y)$ と $(a,b)$ の距離が限りなく $0$ に近づくこと.
i.e.:$\sqrt{(x-a)^{2}+(y-b)^{2}}\rightarrow 0$
極限が存在するならば, 極限値は近づき方によらずに一意的である.
Contents
極限値の求め方
これまで1変数関数の場合, $x=a$ における極限値を求める場合, 左側極限と右側極限
$$\lim_{x\rightarrow a-0}f(x),\ \ \ \lim_{x\rightarrow a+0}f(x)$$
を考えれば良かった.
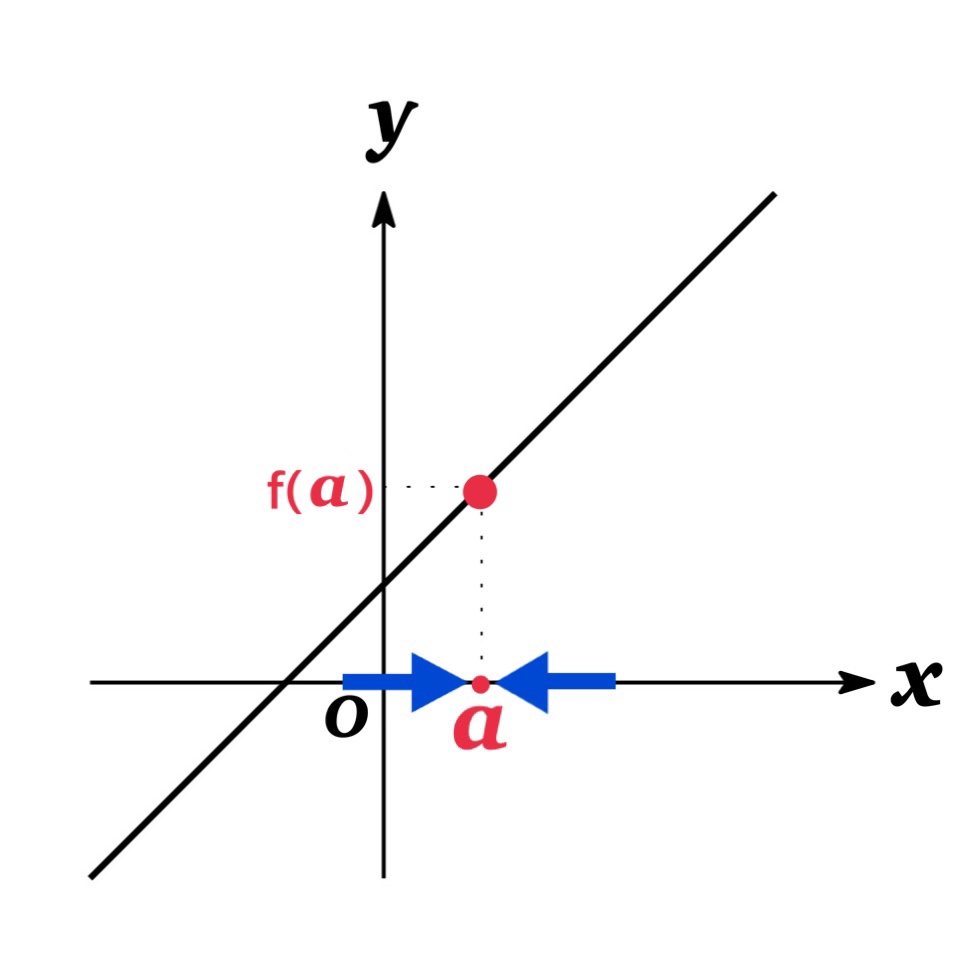
しかし2変数関数の場合は, $(x,y)=(a,b)$ 近づき方が何通りも存在する.
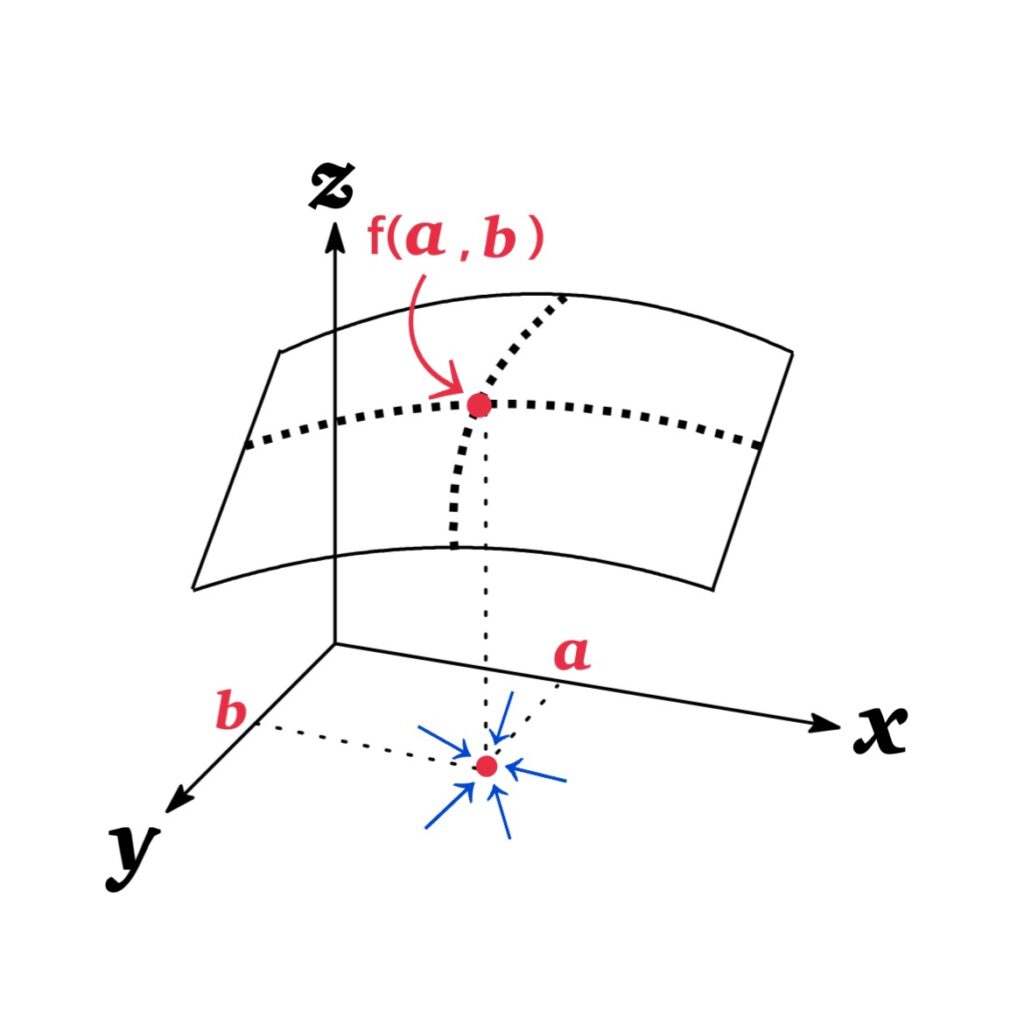
2変数関数の極限値を場合は, 以下の3つの求め方のどれかを用いることが有効となる:
(1)式変形
(2)極座標に変換
(3)$y=mx$ とおく. ($(x,y)\rightarrow (0,0)$のときのみ有効.)
極限値が存在する場合(具体例)
式変形
$\displaystyle\lim_{(x,y)\rightarrow (1,1)}\frac{x^{2}-5xy+4y^{2}}{x-y}$ を求めよ.
$\begin{eqnarray*}\displaystyle\lim_{(x,y)\rightarrow (1,1)}\frac{x^{2}-5xy+4y^{2}}{x-y}&=&\displaystyle\lim_{(x,y)\rightarrow (1,1)}\frac{(x-4y)(x-y)}{x-y}\\&=&\displaystyle\lim_{(x,y)\rightarrow (1,1)}x-4y\\&=&-3\end{eqnarray*}$
極座標変換
$\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{x^{2}y}{x^{2}+y^{2}}$ を求めよ.
$x=r\cos\theta,\ y=r\sin\theta$ と極座標に変換する.
$\begin{eqnarray*}\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{x^{2}y}{x^{2}+y^{2}}&=&\displaystyle\lim_{r\rightarrow 0}\frac{(r\cos\theta)^{2}r\sin\theta}{r^{2}(\cos^{2}\theta+\sin^{2}\theta)}\\&=&\displaystyle\lim_{r\rightarrow 0}r\cos^{2}\theta\sin\theta\end{eqnarray*}$
このとき $|\sin\theta|\leq 1,\ |\cos\theta|\leq 1$ より,
$|r\cos^{2}\theta\sin\theta|\leq r$
「$\displaystyle\lim_{r\rightarrow 0}r$」 と「はさみうちの定理」より
$\displaystyle\lim_{r\rightarrow 0}r\cos^{2}\theta\sin\theta=0$
補足:一般に $(x,y)\rightarrow (a,b)$のとき
$\begin{cases}x=a+r\cos\theta & \\y=b+r\sin\theta &\end{cases}$
とおいて, $r\rightarrow 0$ を考えればよい.
$y=kx$ とおく
$\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{x^{2}y}{x^{2}+y^{2}}$ を求めよ.
$y=kx$ とおくと
$\begin{eqnarray*}\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{xy}{x^{2}+y^{2}}&=&\displaystyle\lim_{x\rightarrow 0}\frac{x^{2}(kx)}{x^{2}+(kx)^{2}}\\&=&\displaystyle\lim_{x\rightarrow 0}\frac{kx}{1+k^{2}}\\&=&0\end{eqnarray*}$
よって$\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{x^{2}y}{x^{2}+y^{2}}=0$ となる.
極限値が存在しない場合(具体例)
極座標変換
$\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{xy}{x^{2}+y^{2}}$ を求めよ.
$x=r\cos\theta,\ y=r\sin\theta$ と極座標に変換する.
$\begin{eqnarray*}\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{xy}{x^{2}+y^{2}}&=&\displaystyle\lim_{r\rightarrow 0}\frac{(r\cos\theta)(r\sin\theta)}{r^{2}(\cos^{2}\theta+\sin^{2}\theta)}\\&=&\displaystyle\lim_{r\rightarrow 0}\cos\theta\sin\theta\end{eqnarray*}$
このとき極限値は $\theta$ の値に依存している.
よって一意的ではないので, 極限は存在しない.
$y=kx$ とおく
$\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{xy}{x^{2}+y^{2}}$ を求めよ.
$y=kx$ とおくと
$\begin{eqnarray*}\displaystyle\lim_{(x,y)\rightarrow (0,0)}\frac{xy}{x^{2}+y^{2}}&=&\displaystyle\lim_{x\rightarrow 0}\frac{x(kx)}{x^{2}+(kx)^{2}}\\&=&\displaystyle\lim_{x\rightarrow 0}\frac{k}{1+k^{2}}\end{eqnarray*}$
このとき極限値は$k$ の値に依存している.
よって一意的ではないので, 極限は存在しない.
厳密な極限値の定義
任意の$\epsilon >0$ に対して, ある$\delta >0$ が存在して
$$\sqrt{(x-a)^{2}+(y-b)^{2}}<\delta\ \ \ \Longrightarrow \ \ \ |f(x,y)-c|<\epsilon$$
が成り立つとき,$c$ を $(x,y)\rightarrow (a,b)$ のときの $f(x,y)$ の極限値であるという.
どのような $\epsilon$ をとってきても, $ |f(x)-f(a)|<\epsilon$ を満たすような $\delta$ を見つければよい.
$\delta$ は $\epsilon$ や $a$ を用いて表されることになる.