The inverse functions of the sine, cosine, and tangent are defined as below: \begin{eqnarray*}\sin^{-1} x=y &\Longleftrightarrow & \sin y=x\ \ \ \ \ (-\frac{\pi}{2}\leq y\leq \frac{\pi}{2})\\\cos^{-1} x=y &\Longleftrightarrow & \cos y=x\ \ \ \ \ ( 0 \leq y \leq \pi ) \\\tan^{-1} x=y &\Longleftrightarrow & \tan y=x\ \ \ \ \ (-\frac{\pi}{2} < y < \frac{\pi}{2})\end{eqnarray*}
The trigonometric functions are not one-to-one, therefore they do not have inverse functions.
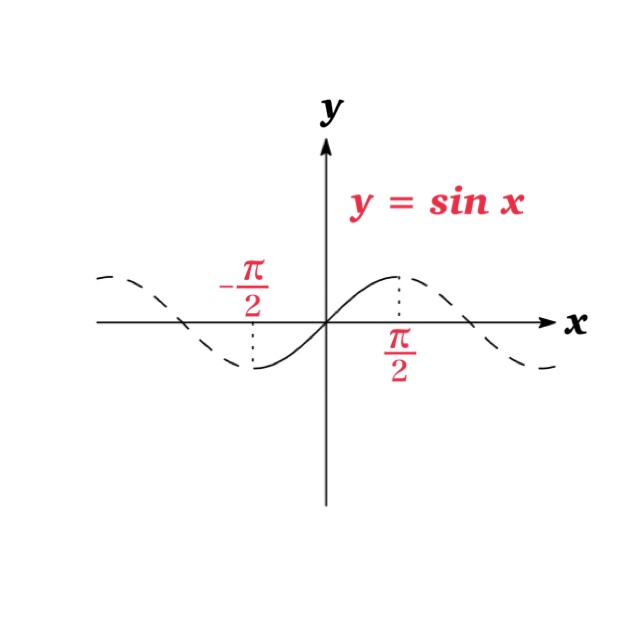
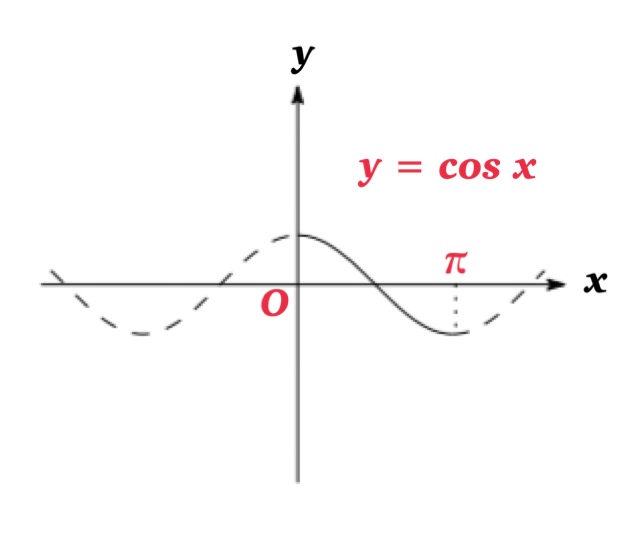
However, it is possible to restrict the domain of trigonometric functions so that they become one-to-one and the inverse functions of these restricted trigonometric functions can be defined.
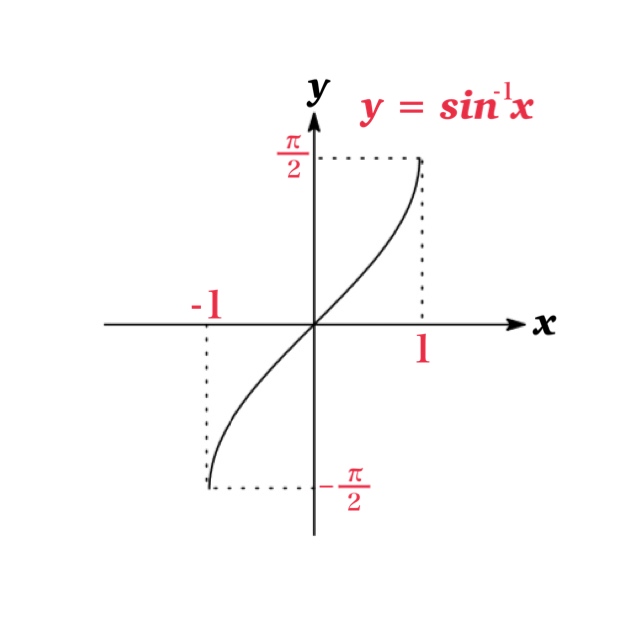
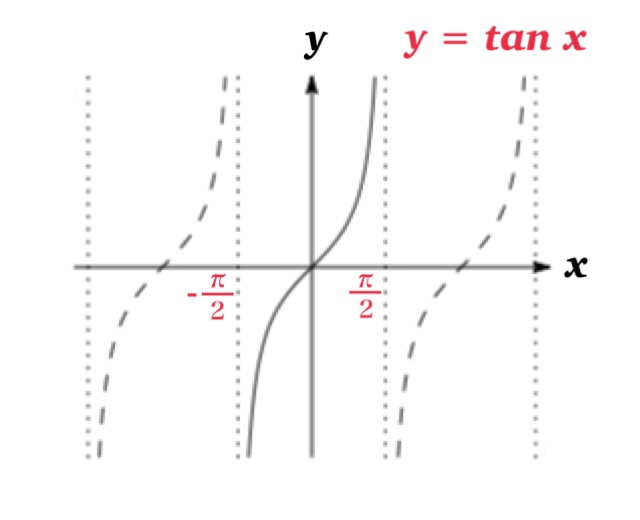
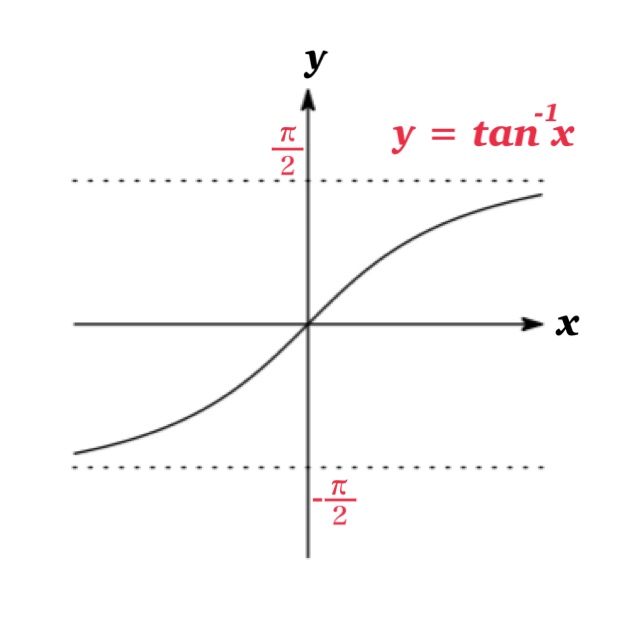
| Inverse Trigonometric Functions | Domain | Range |
| Inverse sine function \(y=\sin^{-1} x\) | \(-1\leq x\leq 1\) | \(-\frac{\pi}{2}\leq y\leq \frac{\pi}{2}\) |
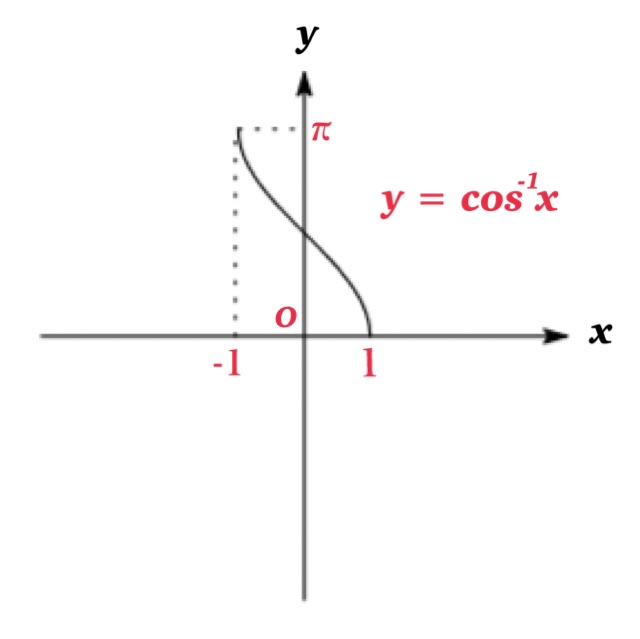
| Inverse cosine function \(y=\cos^{-1} x\) | \(-1\leq x\leq 1\) | \(0\leq y\leq \pi\) |
| Inverse tangent function \(y=\tan^{-1} x\) | \(-\infty \)<\( x< \infty\) | \(-\frac{\pi}{2}\) < \( y\) < \(\frac{\pi}{2}\) |
Symmetry
| $\sin^{-1}(-x)=-\sin^{-1}x$ |
| $\tan^{-1}(-x)=-\tan^{-1}x$ |
Notice:$\cos^{-1}(-x)\not=-\sin^{-1}x$
Derivatives
| $\frac{d}{dx} (\sin^{-1} x)=\frac{1}{\sqrt{1-x^{2}}}$ |
| $\frac{d}{dx} (\cos^{-1} x)=-\frac{1}{\sqrt{1-x^{2}}}$ |
| $\frac{d}{dx} (\tan^{-1} x)=\frac{1}{1+x^{2}}$ |
| $\frac{d}{dx} (\sin^{-1} f(x))=\frac{f'(x)}{\sqrt{1-{f(x)}^{2}}}$ |
| $\frac{d}{dx} (\cos^{-1} f(x))=-\frac{f'(x)}{\sqrt{1-{f(x)}^{2}}}$ |
| $\frac{d}{dx} (\tan^{-1} f(x))=\frac{f'(x)}{1+f(x)^{2}}$ |
Integration
| $\int \frac{1}{\sqrt{1-x^{2}}}\ dx=\sin^{-1}x +C$ |
| $\int \frac{1}{\sqrt{1-x^{2}}}\ dx=-\cos^{-1}x +C$ |
| $\int \frac{1}{1+x^{2}}\ dx=\tan^{-1}x +C$ |
| $\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx=\frac{1}{p}\sin^{-1}\frac{px+q}{a} +C$ |
| $\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx=-\frac{1}{p}\cos^{-1}\frac{px+q}{a} +C$ |
| $\int \frac{1}{a^{2}+(px+q)^{2}}\ dx=\frac{1}{ap}\tan^{-1}\frac{px+q}{a} +C$ |