Contents
Definition
We define \( y=\sin^{-1} x \) ( or \(arc\sin x \) ) to be the inverse function of \(y=\sin x\) . That is
$$y=\sin^{-1} x \Longleftrightarrow x=\sin y$$ where \(-\frac{\pi}{2} \leq y \leq\frac{\pi}{2}\).
Note that \(y=\sin x\) is not one to one, therefore we restrict the interval on \(-\frac{\pi}{2} \leq x \leq\frac{\pi}{2}\).
Then, the graph of \(y=\sin x\) on the interval \([-\frac{\pi}{2}, \frac{\pi}{2}]\) is one-to-one, and the range of the function \(y=\sin x\) is \(-1\leq y \leq 1\).
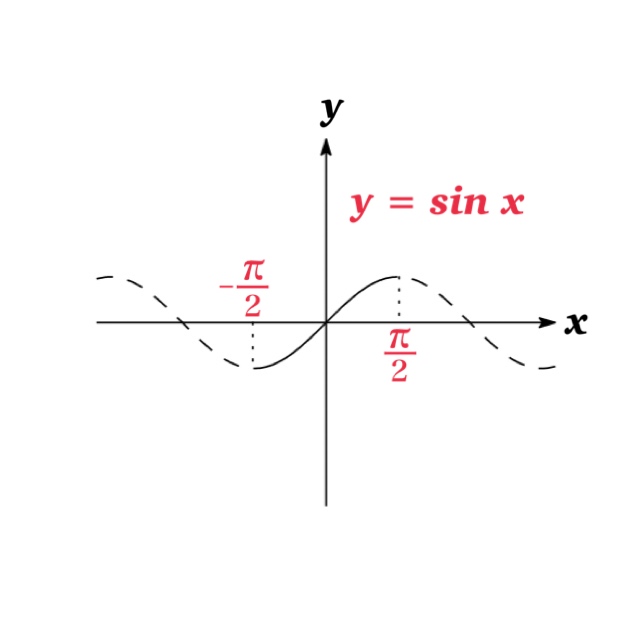
Then we define the inverse function of this restricted sine function which is denoted by \( \sin^{-1} x \) or \(\arcsin x \).
The domain of the function \(y=\sin^{-1} x\) is \([-1,1]\) which is the range of \(y=\sin x\), and the range of the function \(y=\sin^{-1} x\) is \([-\frac{\pi}{2}, \frac{\pi}{2}]\) which is the domain of \(y=\sin x\).
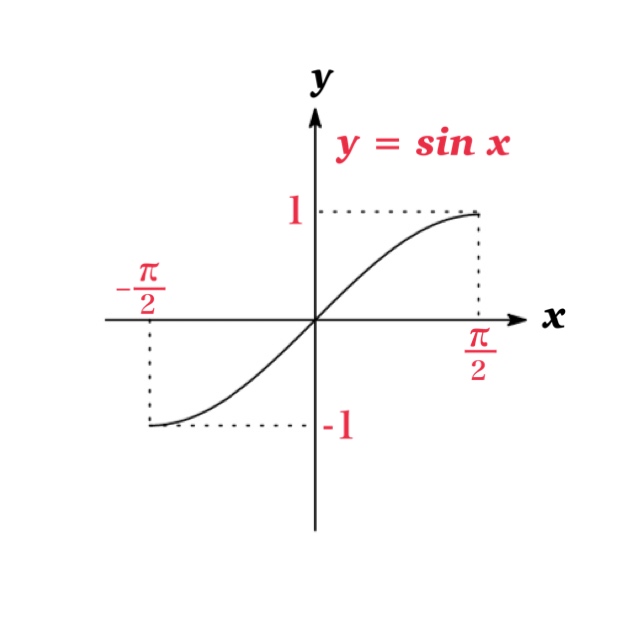
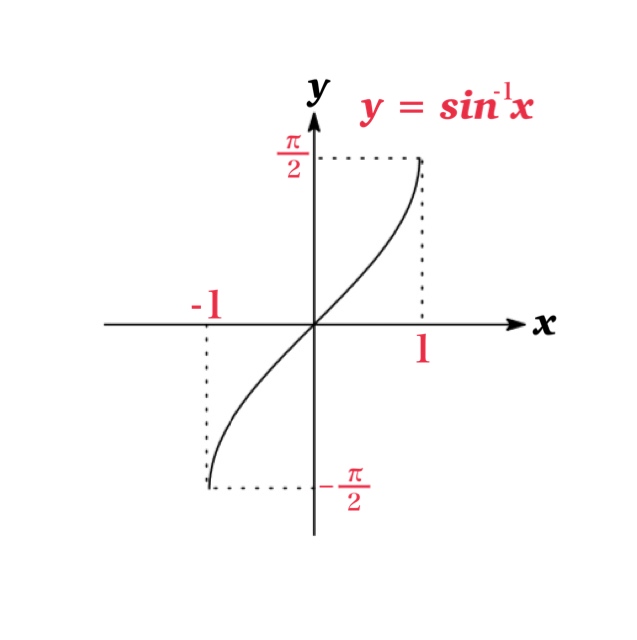
Example
Evaluate \(\sin^{-1}(\frac{1}{2}),\ \sin^{-1}(\frac{\sqrt{2}}{2})\), and \(\sin^{-1}(-\frac{1}{2})\).
Solution: We have $$\sin^{-1}(\frac{1}{2})=\frac{\pi}{6},\ \ \sin^{-1}(\frac{\sqrt{2}}{2})=\frac{\pi}{4},\ \ \ \text{and}\ \ \ \sin^{-1}(-\frac{1}{2})=-\frac{\pi}{6}$$
since \(\sin(\frac{\pi}{6})=\frac{1}{2}, \sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}\) and \(\sin(-\frac{\pi}{6})=-\frac{1}{2}\). Notice that \(\sin^{-1}(-x)=-\sin^{-1} x\).
Cancellation Equation
\begin{eqnarray*}&&\sin^{-1}(\sin x)=x\ \ \ \ \ ( -\frac{\pi}{2}\leq x \leq\frac{\pi}{2})\\&&\sin(\sin^{-1} x)=x\ \ \ \ \ ( -1\leq x \leq 1)\end{eqnarray*}
Notice that when we use the first cancellation equation, it is valid only when \(-\frac{\pi}{2}\leq x \leq\frac{\pi}{2}\). See examples how to proceed when x lies outside this interval.
Example
Evaluate \(\sin^{-1}(\sin \frac{\pi}{3})\) and \(\sin^{-1}(\sin\frac{2\pi}{3})\).
Solution: \(\sin^{-1}(\sin \frac{\pi}{3})=\frac{\pi}{3}\) since \(\frac{\pi}{3}\) lies between \(-\frac{\pi}{2}\leq x \leq\frac{\pi}{2}\).
The other hand, since \(\frac{2\pi}{3}\) does not lie between \(-\frac{\pi}{2}\leq x \leq\frac{\pi}{2}\), we can not use the cancellation equation. Then we extend the equation as below:
$$\sin^{-1}(\sin\frac{2\pi}{3})=\sin^{-1}(\frac{\sqrt{3}}{2})=\frac{\pi}{3}$$
and \(\frac{\pi}{3}\) lies between \(-\frac{\pi}{2}\leq x \leq\frac{\pi}{2}\).
Derivatives
\begin{eqnarray*}&&\frac{d}{dx} (\sin^{-1} x)=\frac{1}{\sqrt{1-x^{2}}}\ \ \ \ \ (|x|<1)\\ &&\frac{d}{dx} (\sin^{-1} f(x))=\frac{f'(x)}{\sqrt{1-\{f(x)\}^{2}}}\ \ \ \ \ (|f(x)|<1)\end{eqnarray*}
Let \(y=\sin^{-1} x\). Then \(y=\sin^{-1} x\) if and only if \(x=\sin y\) where \(-\frac{\pi}{2}\leq y\leq\frac{\pi}{2}\).
Therefore, by implicit differentiation
$$\begin{eqnarray*}\frac{d}{dx}(\sin^{-1} x)&=&\frac{dy}{dx}=\frac{1}{\ \ \frac{dx}{dy}\ \ }\\&=&\frac{1}{\frac{d}{dy}(\sin y)}=\frac{1}{\cos y}\end{eqnarray*}$$
By the definition of \(y=\sin^{-1} x\), interval of y is on \(-\frac{\pi}{2}\leq y\leq\frac{\pi}{2}\). Thus, \(\cos y\geq 0\).
Therefore, \(\cos y=+\sqrt{1-\sin^{2} y}=\sqrt{1-x^{2}}\). So, we have shown that
$$\frac{d}{dx} (\sin^{-1} x)=\frac{1}{\sqrt{1-x^{2}}}$$
By applying the Chain Rule, we have
$$\frac{d}{dx} (\sin^{-1} f(x))=\frac{f'(x)}{\sqrt{1-{f(x)}^{2}}}\ \ \ \ \ (|f(x)|<1)$$
Example
Find \(F'(x)\) if \(F(x)=\sin^{-1}3x\).
Solution: \(F'(x)=\frac{1}{\sqrt{1-(3x)^{2}}}\frac{d}{dx}(3x)=\frac{3}{\sqrt{1-9x^{2}}}\).
Integration
By the derivatives formula, we have integration formulas as below:
\begin{eqnarray*}&&\int \frac{1}{\sqrt{1-x^{2}}}\ dx=\sin^{-1}x +C \\
&&\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx=\frac{1}{p}\sin^{-1}\frac{px+q}{a} +C\end{eqnarray*}
Notice that \(\int \frac{1}{\sqrt{1-x^{2}}}\ dx=\sin^{-1}x +C =-\cos^{-1}x +C\).
To evaluate \(\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx\), we rewrite as the following:
\begin{eqnarray*}\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx&=&\int \frac{(\frac{px+q}{a})’ \cdot \frac{a}{p}}{a\sqrt{1-(\frac{px+q}{a})^{2}}}\ dx\\&=&\int \frac{1}{p}\frac{(\frac{px+q}{a})’}{a\sqrt{1-(\frac{px+q}{a})^{2}}}\ dx\\&=&\frac{1}{p}\sin^{-1}(\frac{px+q}{a})+C\end{eqnarray*}
Or substituting \(t=\frac{px+q}{a}\), we have \(\frac{dt}{dx}=\frac{p}{a}\) and \(dt=\frac{p}{a}dx\). Then
\begin{eqnarray*}\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx&=&\frac{1}{p}\int \frac{1}{\sqrt{1-(\frac{px+q}{a})^{2}}}\ \frac{p}{a}dx\\&=&\frac{1}{p}\int \frac{1}{\sqrt{1-t^{2}}}\ dt\\&=&\frac{1}{p}\sin^{-1} t +C\\&=&\frac{1}{p}\sin^{-1}(\frac{px+q}{a})+C\end{eqnarray*}
Example
Evaluate (1) \(\int \frac{1}{\sqrt{9-16x^{2}}}\ dx\) and (2) \(\int \frac{1}{\sqrt{1+x-x^{2}}}\ dx\)
Solution:
(1) \(\int \frac{1}{\sqrt{9-16x^{2}}}\ dx=\int \frac{1}{\sqrt{3^{2}-(4x)^{2}}}\ dx=\frac{1}{4}\sin^{-1}\frac{4}{3}x+C\)
(2)\begin{eqnarray*}\int \frac{1}{\sqrt{1+x-x^{2}}}\ dx&=&\int \frac{1}{\sqrt{1-(x^{2}-x)}}\ dx\ \ \ (*)\\&=&\int \frac{1}{\sqrt{\frac{5}{4}-(x-\frac{1}{2})^{2}}}\ dx\\&=&\int \frac{1}{\sqrt{(\frac{\sqrt{5}}{2})^{2}-(x-\frac{1}{2})^{2}}}\ dx\ \ \ (**)\\&=&\sin^{-1}\frac{2x-1}{\sqrt{5}}+C\end{eqnarray*}
(*)\begin{eqnarray*}&&1+x-x^{2}\\&=&-(x^{2}-x)+1\\&=&-(x^{2}-x+\frac{1}{4})+\frac{5}{4}\\&=&-(x-\frac{1}{2})^{2}+\frac{5}{4}
\end{eqnarray*}
(**)$$\frac{x-\frac{1}{2}}{\frac{\sqrt{5}}{2}}=\frac{2x-1}{\sqrt{5}}$$