Let f be a one to one function. Then we define \(y=f^{-1} (x)\) to be the inverse function of \(y=f(x)\). That is
$$y=f^{-1}(x) \ \ \Longleftrightarrow \ \ f(y)=x$$
Example: If \(f(3)=5\) and \(f(5)=7\), then \(f^{-1}(5)=3\) and \(f^{-1}(7)=5\).
The definition of the inverse function says that if \(f\) maps x into y, then \(f^{-1}\) maps y back into x. That is, the inverse function reverse inputs and outputs. Therefore we see that
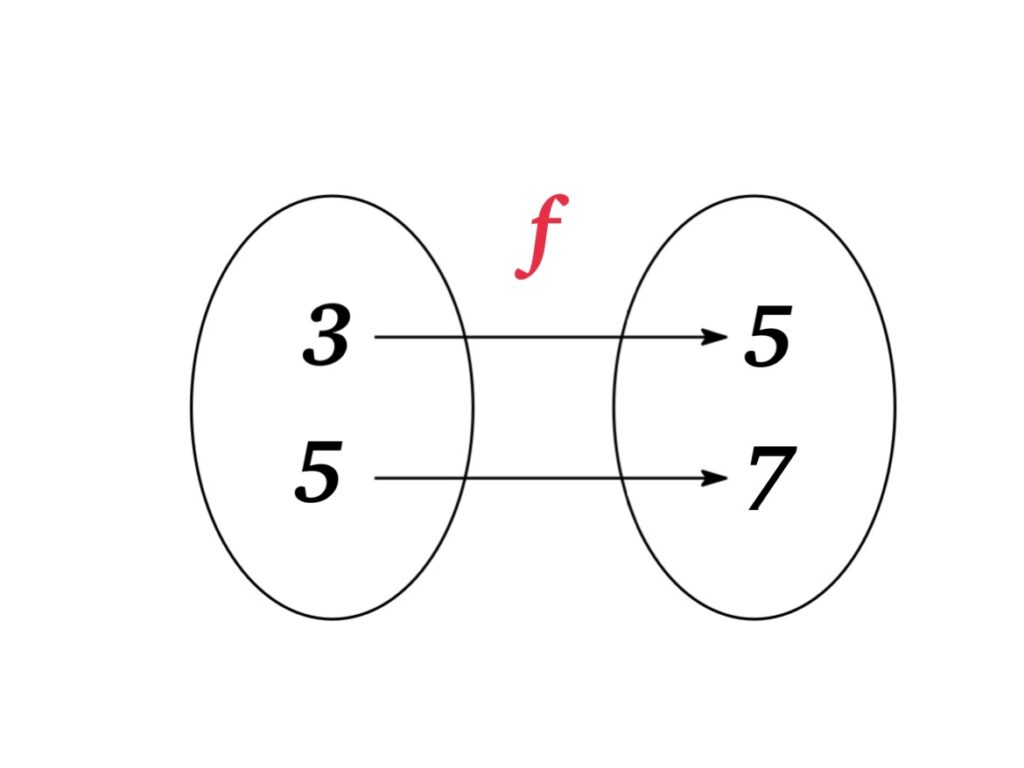
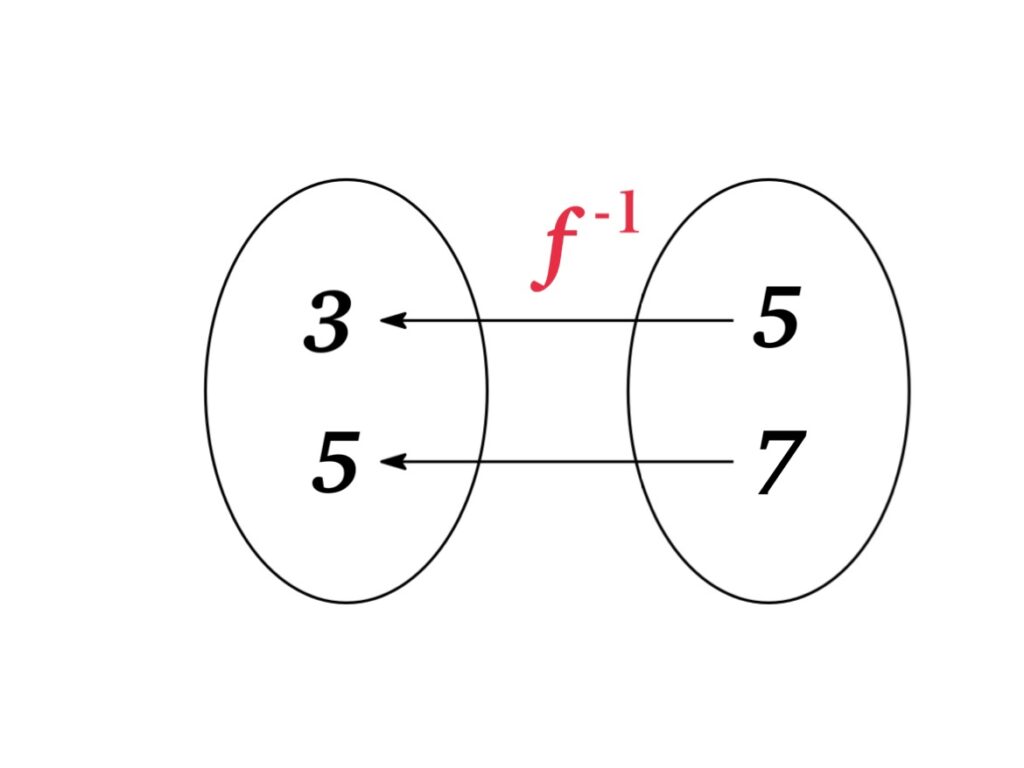
\begin{eqnarray*}&&\text{domain of } f^{-1} = \text{range of } f\\&&\text{range of } f^{-1} = \text{domain of } f\end{eqnarray*}
Remark
Not every function has an inverse function. The definition says that the condition of a function \(f\) to have an inverse function \(f^{-1}\) must satisfy is that \(f\) is one-to-one.
Since if \(f\) were not one-to-one, \(f^{-1}\) would not be uniquely defined.
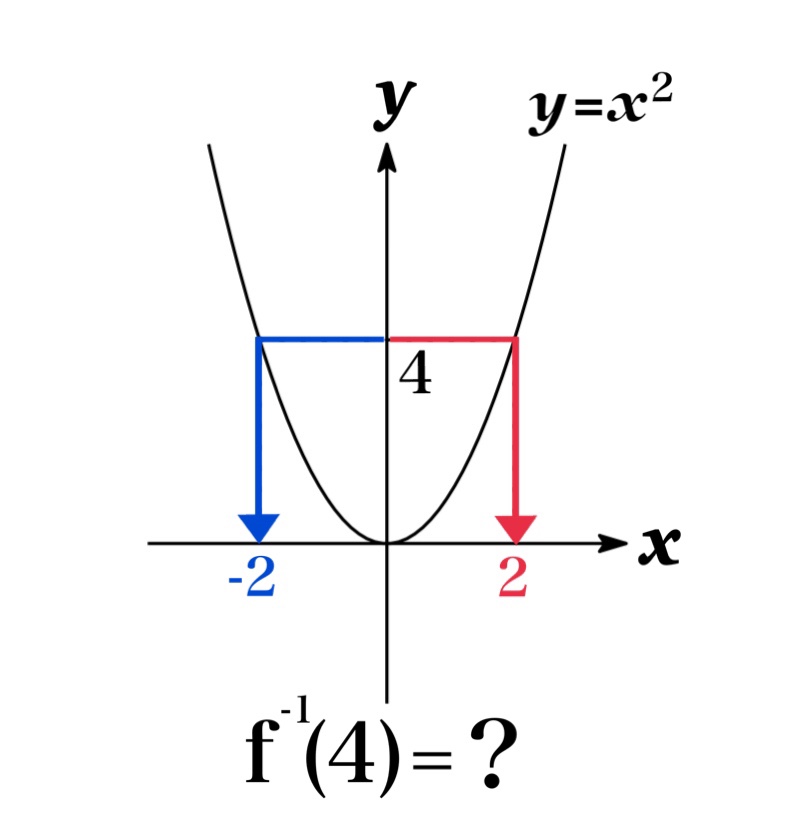
For example, the function \(f(x)=x^{2}\) does not posses an inverse function. Since \(f(2)=4=f(-2)\), an inverse \(f^{-1}(x)\) have to satisfy \(f^{-1}(4)=2\) and \(f^{-1}(4)=2\) which is impossible.
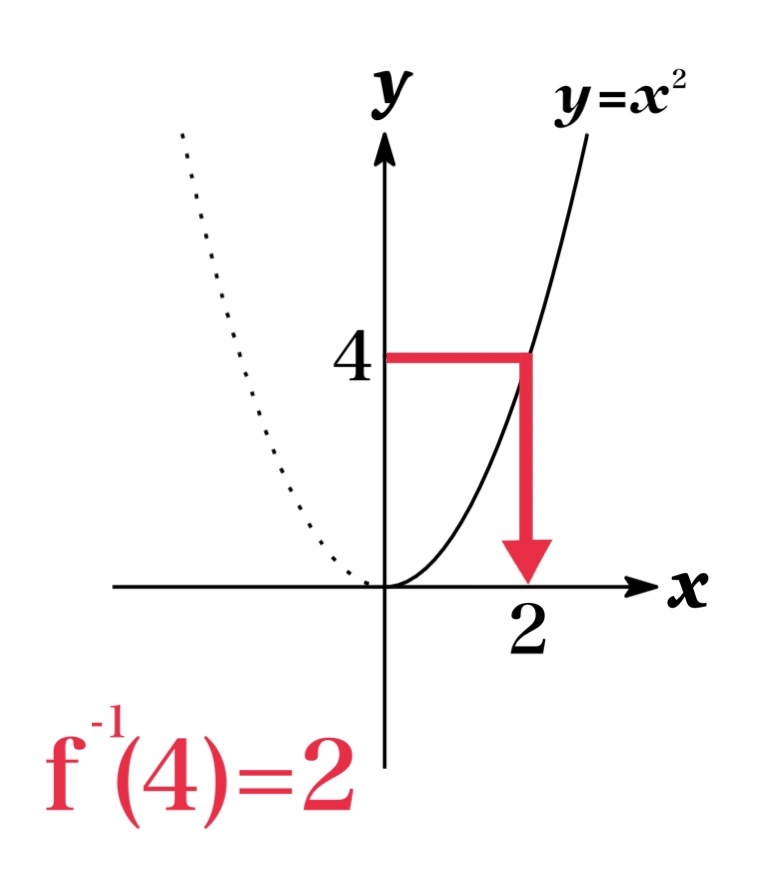
However, if we restricted the domain of \(f(x)=x^{2}\) on \(x\geq 0\), then the restricted function would have an inverse function \(f^{-1}(x)\).
How to find the inverse function?
(Step 1) Write \(y=f(x)\).
(Step 2) Solve this equation for \(x\)
(Step 3) To express inverse function \(f^{-1} \) as a function of \(x\), interchange x and y.
The resulting equation is \(y=f^{-1}(x)\).
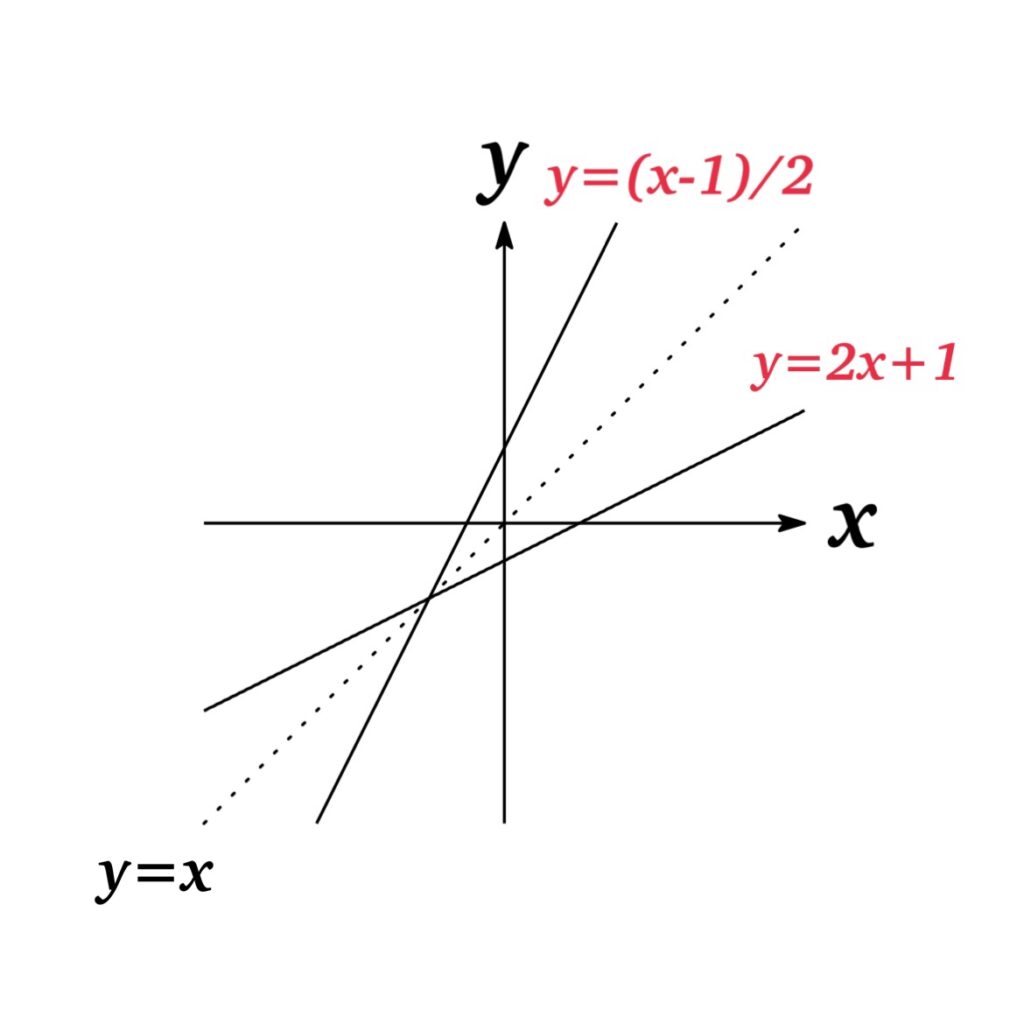
Example: Find the inverse function of \(f(x)=2x+1\).
(Step 1) We first write \(f(x)=2x+1\) as
$$y=2x+1$$
(Step 2) Solve this equation for \(x\) :
\begin{eqnarray*}2x&=&y-1\\x&=&\frac{y-1}{2}\end{eqnarray*}
(Step 3) Interchange x and y.
$$y=\frac{x-1}{2}$$
Therefore, the inverse function of \(f(x)=2x+1\) is \(f^{-1}(x)=\frac{x-1}{2}\).
Graphs
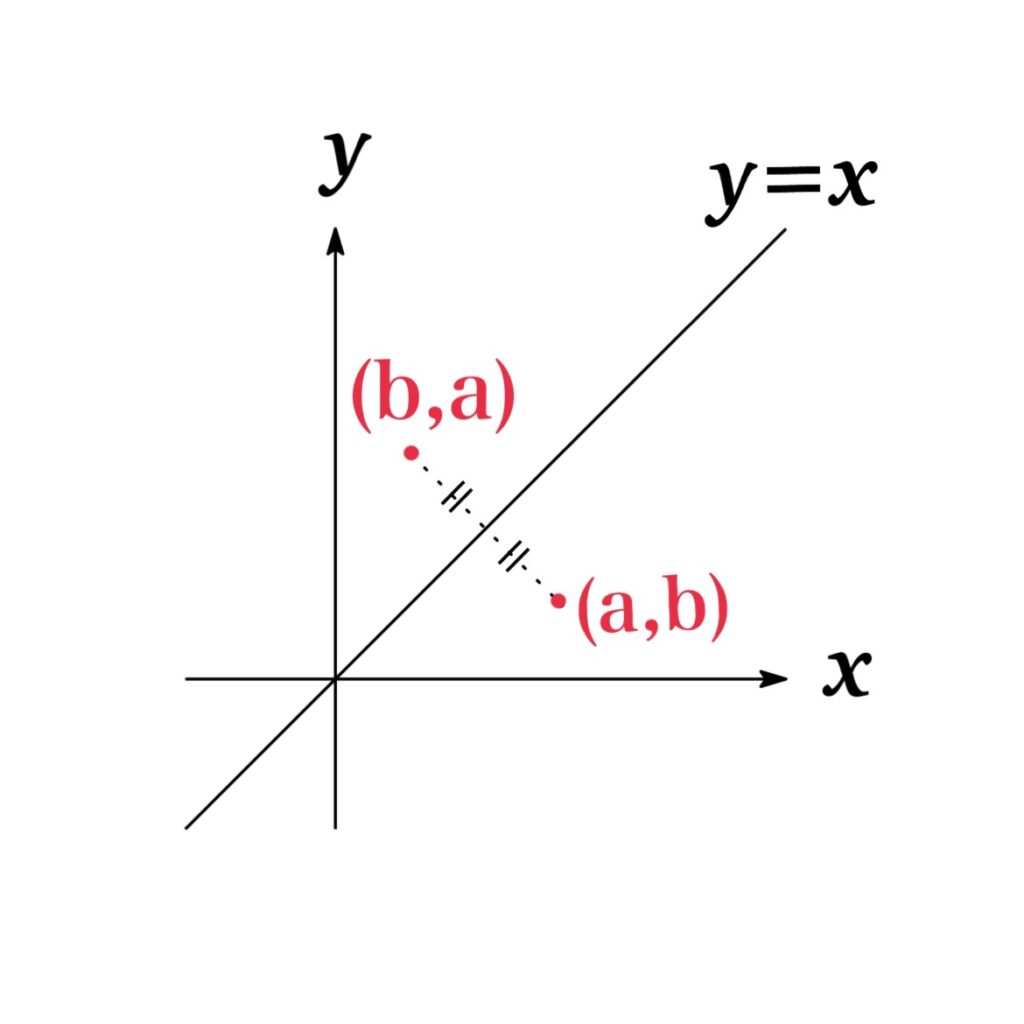
The graph of \(f\) and \(f^{-1}\) are symmetric with respect to \(y=x\).
Since the definition of the inverse function, \(f(a)=b\) if and only if \(f^{-1}(b)=a\). That is, the point \((a,b)\) is on the graph of \(f\) if and only if the point \((b,a)\) is on the graph of \(f^{-1}\).
Furthermore, we get the point \((b,a)\) from \((a, b)\) by reflecting about the line \(y=x\). Thus the graph of the inverse function \(f^{-1}\) is obtained by reflecting the graph of \(f\) about the line \(y=x\).
Derivative
If \(f\) is differentiable, then \(f^{-1}\) is differentiable and \((f^{-1})’\) is given by
$$\frac{d}{dx}f^{-1}(x)=\frac{dy}{dx}=\frac{1}{\ \frac{dx}{dy}\ }=\frac{1}{f'(y)}$$
where \(x=f(y)\) and \(f'(y)\not= 0\)
Differentiate both sides of \(x=f(y)\) with respect to x. Then by the Chain Rule, we have
$$1=f'(y)\cdot y’$$
where \(y=f^{-1}(x)\) and \(y’=\frac{d}{dx}f^{-1}(x)\). Therefore, we obtain
$$\frac{d}{dx}f^{-1}(x)=y’=\frac{1}{f'(y)}$$
Example
If \(f(x)=x^{2}\) with the domain \(0\leq x\), find the derivative of its inverse function \(f^{-1}(x)\).
Solution : Since \(f'(x)=2x\) and \(f^{-1}(x)=\sqrt{x}\), we obtain
$$\frac{d}{dx}f^{-1}(x)=\frac{1}{f'(y)}=\frac{1}{2y}=\frac{1}{2f^{-1}(x)}=\frac{1}{2\sqrt{x}}$$