We define \(y=\cos^{-1} x\) to be the inverse function of \(y=\cos x\). That is
$$y=\cos^{-1} x \ \ \Longleftrightarrow \ \ x=\cos y$$
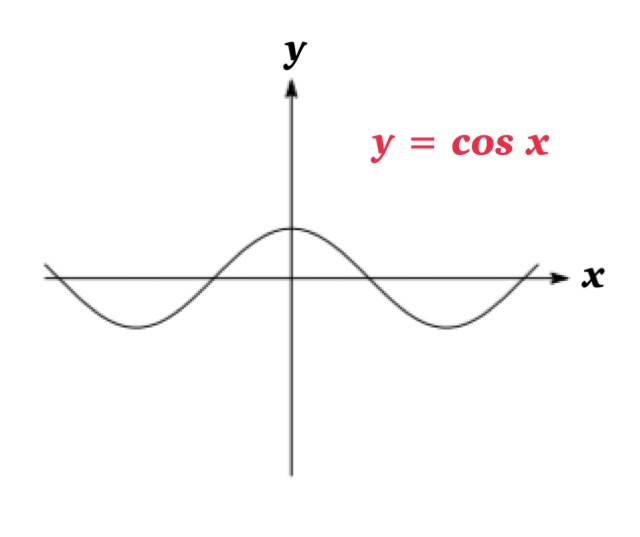
Note that \(y=\cos x\) is not one to one, therefore we restrict the interval on \(0\leq x \leq \pi\).
Then, the graph of \(y=\cos x\) on the interval \([0, \pi]\) is one-to-one, and the range of the function \(y=\cos x\) is \([-1,1]\).
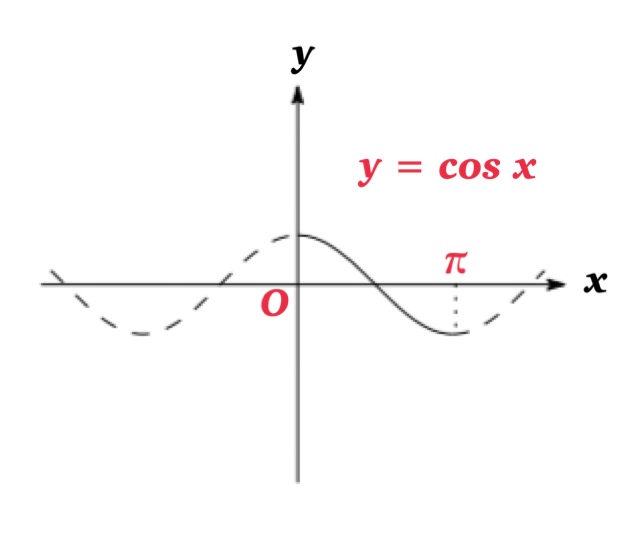
Then we define the inverse function of this restricted cosine function which is denoted by \( \cos^{-1} x \) or \(\arccos x \).
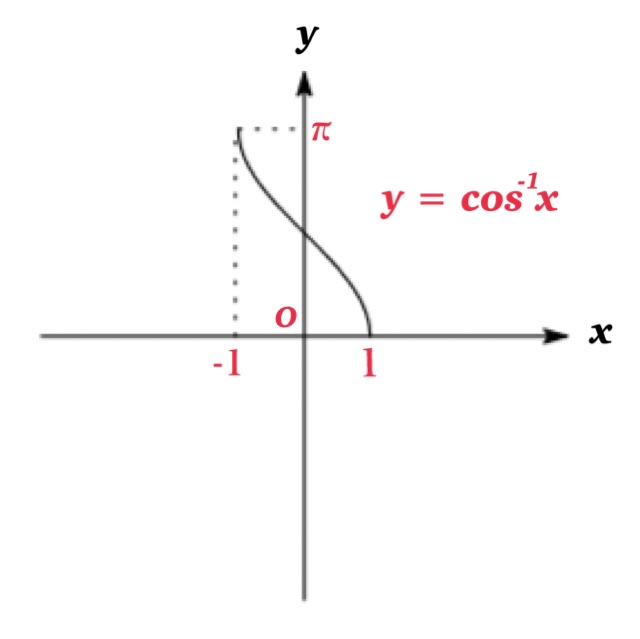
The domain of the function \(y=\cos^{-1} x\) is \([-1,1]\) which is the range of \(y=\cos x\). and the range of the function \(y=\cos^{-1} x\) is \([0, \pi]\) which is the (restricted) domain of \(y=\cos x\).
Notice that we can see that \(\cos^{-1}(-x)\not=-\cos^{-1} x\).

Example : Evaluate \(\cos^{-1}(\frac{1}{2}),\ \cos^{-1}(\frac{\sqrt{2}}{2})\), and \(\cos^{-1}(-\frac{1}{2})\).
Solution: We have $$\cos^{-1}(\frac{1}{2})=\frac{\pi}{3},\ \ \cos^{-1}(\frac{\sqrt{2}}{2})=\frac{\pi}{4},\ \ \ \text{and}\ \ \ \cos^{-1}(-\frac{1}{2})=\frac{2\pi}{3} $$
since \(\cos(\frac{\pi}{3})=\frac{1}{2}, \cos(\frac{\pi}{4})=\frac{\sqrt{2}}{2}\) and \(\cos(\frac{2\pi}{3})=-\frac{1}{2}\).
Derivative
\begin{eqnarray*}&&\frac{d}{dx} (\cos^{-1} x)=-\frac{1}{\sqrt{1-x^{2}}}\ \ \ \ \ (|x|<1)\\ &&\frac{d}{dx} (\cos^{-1} f(x))=-\frac{f'(x)}{\sqrt{1-\{f(x)\}^{2}}}\ \ \ \ \ (|f(x)|<1)\end{eqnarray*}
Let \(y=\cos^{-1} x\). Then \(y=\cos^{-1} x\) if and only if \(x=\cos y\) where \(0 \leq y\leq \pi\).
Therefore, by implicit differentiation
$$\begin{eqnarray*}\frac{d}{dx}(\cos^{-1} x)&=&\frac{dy}{dx}=\frac{1}{\ \ \frac{dx}{dy}\ \ }\\&=&\frac{1}{\frac{d}{dy}(\cos y)}=\frac{1}{-\sin y}\end{eqnarray*}$$
By the definition of \(y=\cos^{-1} x\), y is interval of \(0\leq y\leq\pi\).
Thus, \(\sin y\geq 0\). Therefore, \(\sin y=+\sqrt{1-\cos^{2} y}=\sqrt{1-x^{2}}\)
So, we have shown that
$$\frac{d}{dx} (\cos^{-1} x)=-\frac{1}{\sqrt{1-x^{2}}}$$
By applying the Chain Rule, we have
$$\frac{d}{dx} (\cos^{-1} f(x))=-\frac{f'(x)}{\sqrt{1-{f(x)}^{2}}}$$
Example
Find \(F'(x)\) if \(F(x)=\cos^{-1}x^{2}\).
Solution: \(F'(x)=-\frac{1}{\sqrt{1-(x^{2})^{2}}}\frac{d}{dx}(x^{2})=-\frac{2x}{\sqrt{1-x^{4}}}\).
Integration
By the derivatives formula, we have integration formulas as below:
\begin{eqnarray*}&&\int \frac{1}{\sqrt{1-x^{2}}}\ dx=-\cos^{-1}x +C \\
&&\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx=-\frac{1}{p}\cos^{-1}\frac{px+q}{a} +C\end{eqnarray*}
Notice that \(\int \frac{1}{\sqrt{1-x^{2}}}\ dx =-\cos^{-1}x +C=\sin^{-1}x +C\). More details, see also Inverse Sine Function.