Exponential Functions - Mrs.Mathpedia

Let $a$ is a positive constant. Then a function of the form

$$f(x)=a^{x}$$

is called an exponential function with base $a$.

Contents

1 Rules
2 properties
3 Graphs
4 Comparison
5 Inverse Function
6 Derivatives / Integrals

Rules

$x$	$y=a^{x}$	Example
$x=0$	$a^{0}=1$	$3^{0}=1$
$x=n$, where n is a positive integer.	$a^{n}=\overbrace{a\cdot a\cdots a}^{n\ \text{factors}} $	$2^{3}=2\cdot 2\cdot 2=8$
$x=r$, where r is a real number.	$a^{-r}=\frac{1}{a^{r}}$	$2^{-3}=\frac{1}{2^{3}}=\frac{1}{8}$
$x=\frac{q}{p}$($x$ is a rational number) where $p$ and $q$ are integers and $p>0$	$a^{\frac{q}{p}}=\sqrt[p]{a^{q}}=(\sqrt[p]{a})^{q}$	$2^{\frac{5}{3}}=\sqrt[3]{2^{5}}=(\sqrt[3]{2})^{5}$

properties

Let $a, b >0$ and $n, m$ be real numbers.

Properties	Example
$a^{n+m}=a^{n}a^{m}$	$a^{2}a^{3}=(a\cdot a)\cdot (a\cdot a\cdot a)=a^{2+3}=a^{5}$
$a^{n-m}=\frac{a^{n}}{a^{m}}$	$\frac{a^{5}}{a^{3}}=\frac{a\cdot a\cdot a\cdot a\cdot a}{a\cdot a\cdot a}=a^{5-3}=a^{2}$
$\left(a^{n}\right)^{m}=a^{nm}$	$\left(a^{2}\right)^{3}=a^{2}\cdot a^{2}\cdot a^{2}=a^{2\times 3}=a^{6}$
$(ab)^{n}=a^{n}b^{n}$	$(ab)^{3}=(ab)\cdot (ab)\cdot (ab)=a^{3}b^{3}$

Graphs

Figure 1	If $0<a<1$, $y=a^{x}$ is a decreasing function.
Figure 2	If $a=1$, $y=1^{x}$ is a constant function.
Figure 3	If $1<a$, $y=a^{x}$ is an increasing function.
Figure 4	Notice that $y=\left(\frac{1}{a}\right)^{x}$ is the reflection of the graph of $y=a^{x}$ with the respect to the y-axis, since $(\frac{1}{a})^{x}=\frac{1}{a^{x}}=a^{-x}$

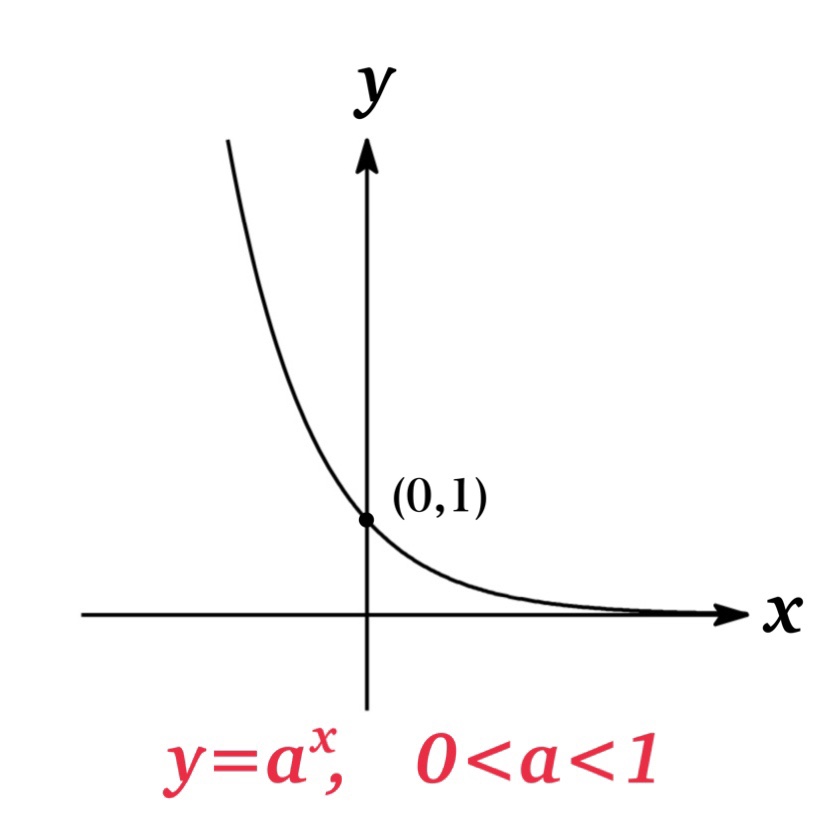
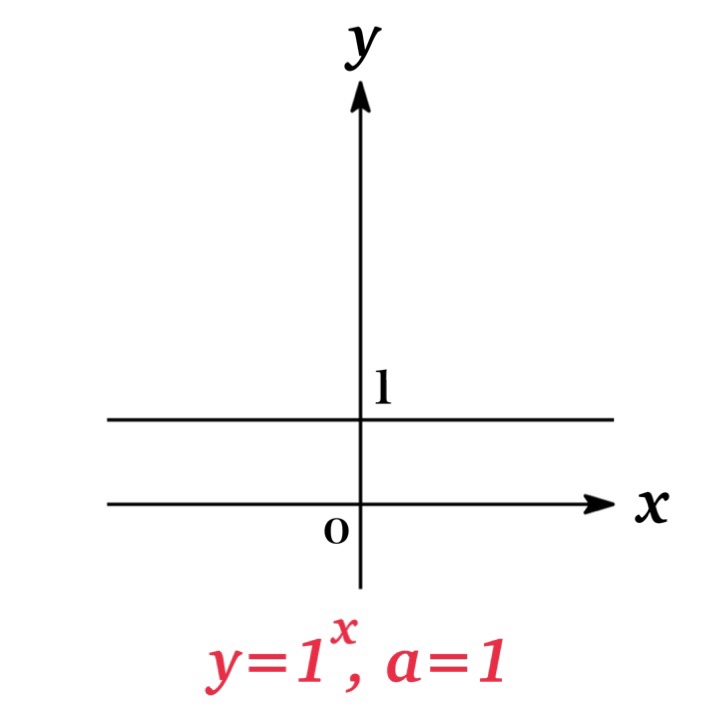
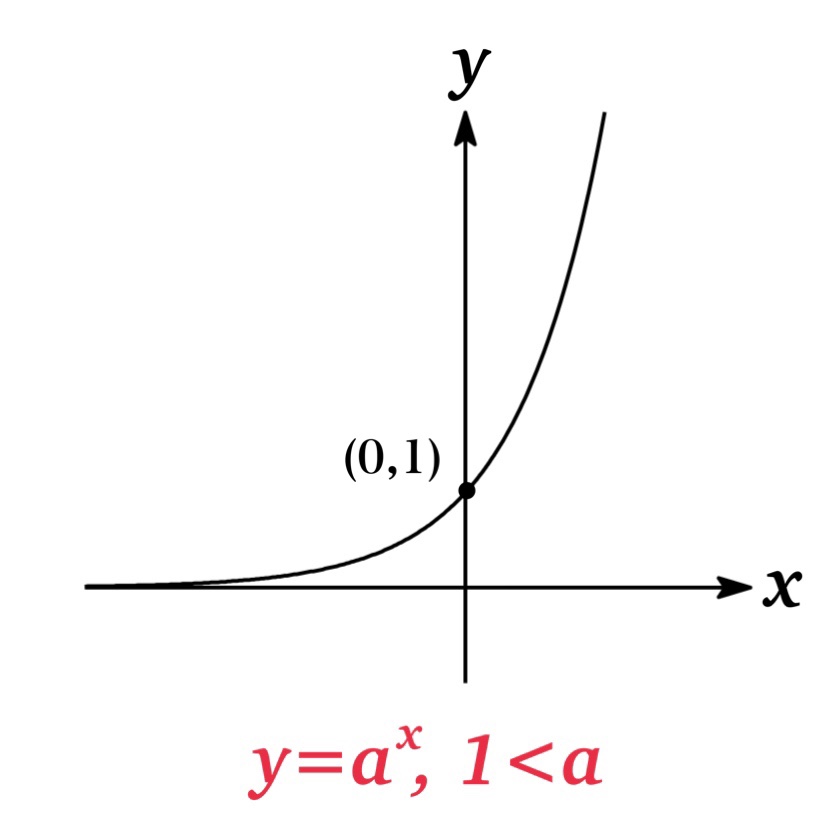
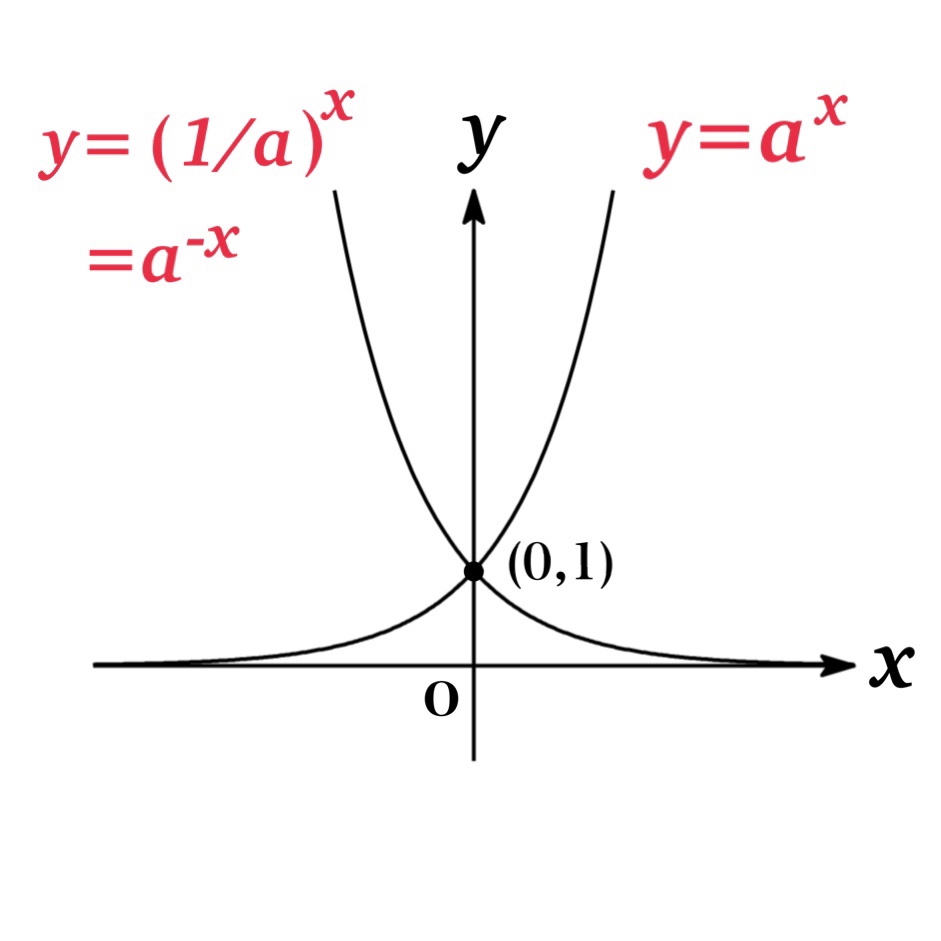
As you see from the graphs, all of $y=a^{x}$ pass through the points$(0,1)$ and $(1,a)$, and the line $y=0$ (that is x-axis) is a horizontal asymptote.

Comparison

$a$	Comparison
$0<a<1$	$x_{1}<x_{2}\ \ \ \longleftrightarrow \ \ \ a^{x_{1}}>a^{x_{2}}$
$a=1$	$a^{x_{1}}=a^{x_{2}}$
$a>1$	$x_{1}<x_{2}\ \ \ \longleftrightarrow \ \ \ a^{x_{1}}<a^{x_{2}}$

Inverse Function

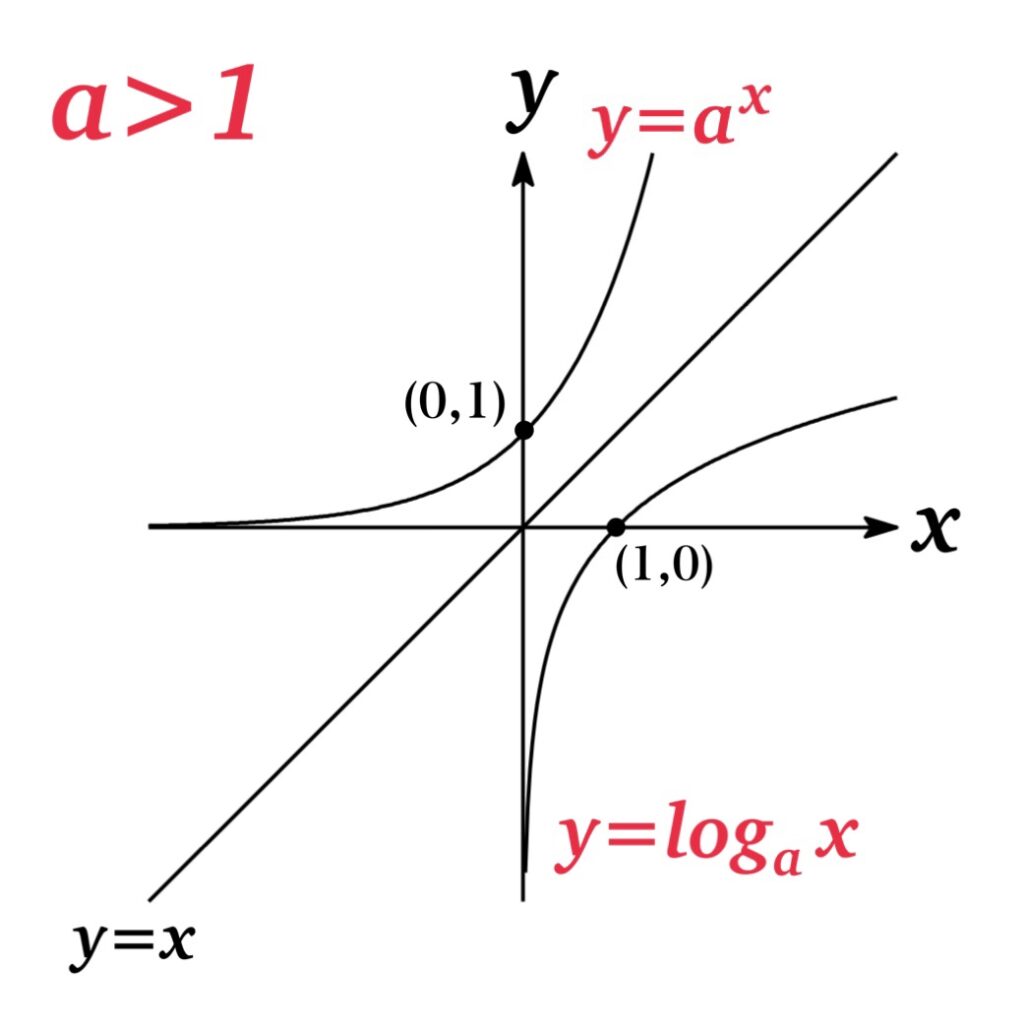
Let a>0 and $a\not=1 $. Then, the inverse function of the exponential function $f(x)=a^{x}$ is defined as the logarithmic function with base a. That is

$$\log_{a} x=y\ \ \ \ \Longleftrightarrow a^{y}=x$$

Notice that if a>0 and $a\not=1 $, the exponential function $f(x)=a^{x}$is either increasing or decreasing. Thus, it is one-to-one and we can define the inverse function of it.

Derivatives / Integrals

$$\frac{d}{dx}[a^{x}]=a^{x}\log_{e} a $$
$$\int a^{x}\ dx=\frac{a^{x}}{\log_{e} a}+C$$

We use the fact that $\mathrm{e}^{\log_{e} a}=a$.

$$\frac{d}{dx}(a^{x})=\frac{d}{dx}(\mathrm{e}^{\log_{e} a})^{x}=\frac{d}{dx}\mathrm{e}^{(\log_{e} a)x}=\mathrm{e}^{(\log_{e} a)x}\frac{d}{dx}(\log_{e} a)x=(\mathrm{e}^{\log_{e} a})^{x}(\log_{e}a)=a^{x}\log_{e} a$$

This can be also proved by using Logarithmic Differentiation Method. By the derivatives formula, we obtain integration formulas as above.

Calculus

\(x\)	\(y=a^{x}\)	Example
\(x=0\)	\(a^{0}=1\)	\(3^{0}=1\)
\(x=n\), where n is a positive integer.	\(a^{n}=\overbrace{a\cdot a\cdots a}^{n\ \text{factors}} \)	\(2^{3}=2\cdot 2\cdot 2=8\)
\(x=r\), where r is a real number.	\(a^{-r}=\frac{1}{a^{r}}\)	\(2^{-3}=\frac{1}{2^{3}}=\frac{1}{8}\)
\(x=\frac{q}{p}\)(\(x\) is a rational number) where \(p\) and \(q\) are integers and \(p>0\)	\(a^{\frac{q}{p}}=\sqrt[p]{a^{q}}=(\sqrt[p]{a})^{q}\)	\(2^{\frac{5}{3}}=\sqrt[3]{2^{5}}=(\sqrt[3]{2})^{5}\)

Properties	Example
\(a^{n+m}=a^{n}a^{m}\)	\(a^{2}a^{3}=(a\cdot a)\cdot (a\cdot a\cdot a)=a^{2+3}=a^{5}\)
\(a^{n-m}=\frac{a^{n}}{a^{m}}\)	\(\frac{a^{5}}{a^{3}}=\frac{a\cdot a\cdot a\cdot a\cdot a}{a\cdot a\cdot a}=a^{5-3}=a^{2}\)
\(\left(a^{n}\right)^{m}=a^{nm}\)	\(\left(a^{2}\right)^{3}=a^{2}\cdot a^{2}\cdot a^{2}=a^{2\times 3}=a^{6}\)
\((ab)^{n}=a^{n}b^{n}\)	\((ab)^{3}=(ab)\cdot (ab)\cdot (ab)=a^{3}b^{3}\)

\(a\)	Comparison
\(0<a<1\)	\(x_{1}<x_{2}\ \ \ \longleftrightarrow \ \ \ a^{x_{1}}>a^{x_{2}}\)
\(a=1\)	\(a^{x_{1}}=a^{x_{2}}\)
\(a>1\)	\(x_{1}<x_{2}\ \ \ \longleftrightarrow \ \ \ a^{x_{1}}<a^{x_{2}}\)

Figure 1	If \(0<a<1\), \(y=a^{x}\) is a decreasing function.
Figure 2	If \(a=1\), \(y=1^{x}\) is a constant function.
Figure 3	If \(1<a\), \(y=a^{x}\) is an increasing function.
Figure 4	Notice that \(y=\left(\frac{1}{a}\right)^{x}\) is the reflection of the graph of \(y=a^{x}\) with the respect to the y-axis, since \((\frac{1}{a})^{x}=\frac{1}{a^{x}}=a^{-x}\)