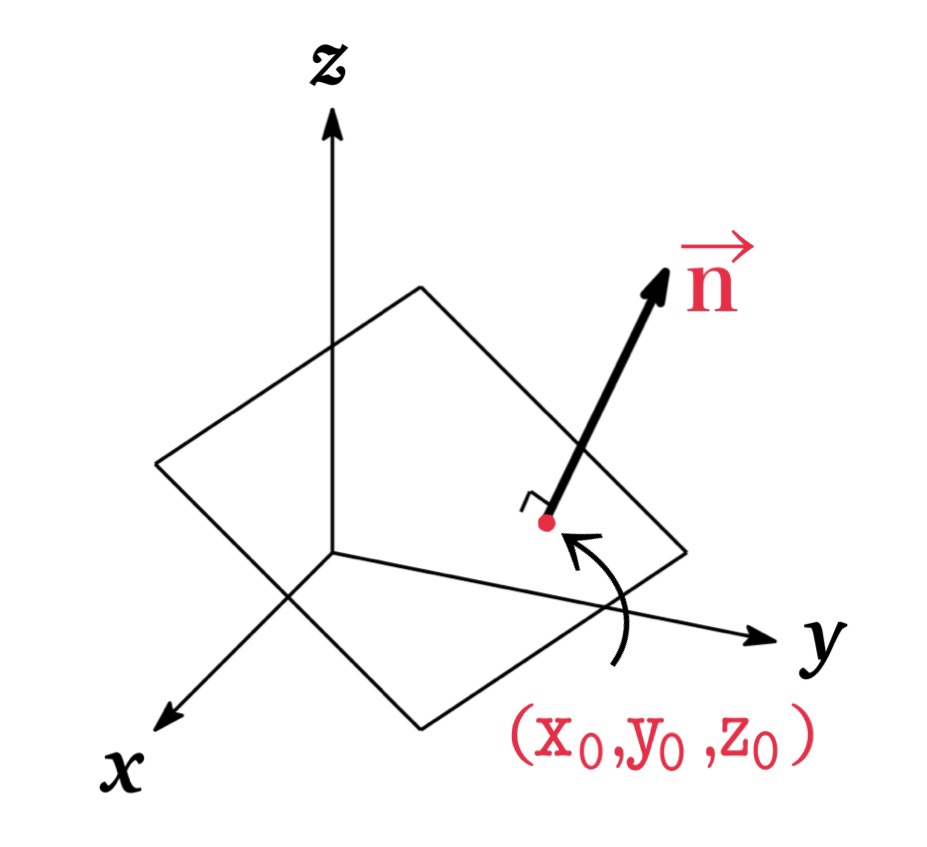
An equation of the plane through \((x_{0},y_{0},z_{0})\) with normal vector \(<a,b,c>\) is given by
$$a(x-x_{0})+b(y-y_{0})+c(z-z_{0})=0\ \ \ \ \ \cdots\ \ \text{(1)}$$
or we can rewrite the equation of a plane (1) as
$$ax+by+cx+d=0\ \ \ \ \ \cdots\ \ \text{(2)}$$
where \(d=-(ax_{0}+by_{0}+c_{0})\).
Notice that it can be shown that if \(a, b\) and \(c\) are not all \(0\), the linear equation (2) represents a plane with normal vector \(<a,b,c>\).
Example
Find the equation of the plane through the points \(P(1,2,3),\ Q(3,5,7)\) and \(R(-1,3,-5)\).
Solution : The vectors \(\overrightarrow{PQ}\) and \(\overrightarrow{PR}\) are
$$\overrightarrow{PQ}=<2,3,4>\ \ \ \ \overrightarrow{PR}=<-2,1,-8>$$
Since both vectors lie in the plane, their cross product \(\overrightarrow{PQ}\times \overrightarrow{PR}\) is orthgonal to the plane and can be taken as the normal vector \(\mathbf{n}\). Thus
$$\mathbf{n}=\overrightarrow{PQ}\times \overrightarrow{PR}=\left|\begin{array}{ccc}\mathbf{i}&\ \mathbf{j}&\ \mathbf{k}\\2& 3& 4\\-2& 1& 8\end{array}\right|=-28\mathbf{i}+8\mathbf{j}+8\mathbf{k}$$
Therefore, an equation of the plane with the point \(P(1,2,3)\) and the normal vector \(\mathbf{n}=<-28,8,8>\) is
$$-28(x-1)+8(y-2)+8(z-3)=0$$
$$\text{or}\ \ \ 7x-2y-2z+3=0$$
Notice that we obtain the same equation of the plane by taking the points \(Q(3,5,7)\) or \(R(-1,3,-5)\).
Proof
A plane in space is determined by a point \(P_{0}(x_{0}, y_{0}, z_{0})\) in the plane and a normal vector \(\mathbf{n}\) which is orthogonal to the plane.
Let \(P(x,y,z)\) be an arbitrary point in the plane with the point \(P_{0}(x_{0},y_{0},z_{0})\) and the normal vector \(\mathbf{n}=<a,b,c>\) .
Then by the property of the dot product, we have that if two vectors \(\overrightarrow{P_{0}P}=<x-x_{0}, y-y_{0},z-z_{0}>\) and \(\mathbf{n}\) are orthogonal,
$$<a,b,c>\cdot <x-x_{0}, y-y_{0},z-z_{0}>=0$$
Thus we obtain
$$a(x-x_{0})+b(y-y_{0})+c(z-z_{0})=0$$

Notice that the normal vector \(\mathbf{n}\) is orthogonal to every vector in the plane.